Newton (unit)
The newton (symbol: N) is the SI derived unit of force, named after Isaac Newton in recognition of his work on classical mechanics.
Contents |
Definition
The newton is the unit of force derived in the SI system; it is equal to the amount of net force required to accelerate a mass of one kilogram at a rate of one meter per second per second. In dimensional analysis, F=ma, multiplying m (kg) by a (m/s2), the dimension for 1 newton unit is therefore:[1]
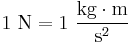
Examples
- 1 N is the force of Earth's gravity on an object with a mass of about 102 g (1⁄9.81 kg) (such as a small apple).
- On Earth's surface, a mass of 1 kg exerts a force of approximately 9.8 N [down] (or 1.0 kilogram-force; 1 kgf=9.80665 N by definition). The approximation of 1 kg corresponding to 10 N is sometimes used as a rule of thumb in everyday life and in engineering.
- The force of Earth's gravity on a human being with a mass of 70 kg is approximately 686 N.
- The dot product of force and distance is mechanical work. Thus, in SI units, a force of 1 N exerted over a distance of 1 m is 1 N·m of work. The Work-Energy Theorem states that the work done on a body is equal to the change in energy of the body. 1 N·m = 1 J (joule), the SI unit of energy.
- It is common to see forces expressed in kilonewtons or kN, where 1 kN = 1,000 N.
Common use of kilonewtons in construction
Kilonewtons are often used for stating safety holding values of fasteners, anchors and more in the building industry.[2] They are also often used in the specifications for rock climbing equipment. The safe working loads in both tension and shear measurements can be stated in kN (kilonewtons).
1 kN equals 101.97162 kilograms of load, but multiplying the kN value by 100 (i.e. using a slightly pessimistic and easier to calculate value) is a good rule of thumb.[3]
Conversion factors
| newton (SI unit) |
dyne | kilogram-force, kilopond |
pound-force | poundal | |
|---|---|---|---|---|---|
| 1 N | ≡ 1 kg·m/s² | = 105 dyn | ≈ 0.10197 kp | ≈ 0.22481 lbF | ≈ 7.2330 pdl |
| 1 dyn | = 10−5 N | ≡ 1 g·cm/s² | ≈ 1.0197×10−6 kp | ≈ 2.2481×10−6 lbF | ≈ 7.2330×10−5 pdl |
| 1 kp | = 9.80665 N | = 980665 dyn | ≡ gn·(1 kg) | ≈ 2.2046 lbF | ≈ 70.932 pdl |
| 1 lbF | ≈ 4.448222 N | ≈ 444822 dyn | ≈ 0.45359 kp | ≡ gn·(1 lb) | ≈ 32.174 pdl |
| 1 pdl | ≈ 0.138255 N | ≈ 13825 dyn | ≈ 0.014098 kp | ≈ 0.031081 lbF | ≡ 1 lb·ft/s² |
| The value of gn as used in the official definition of the kilogram-force is used here for all gravitational units. | |||||
| System | FPS Engineering | FPS Gravitational | FPS Absolute | Metric | |
|---|---|---|---|---|---|
| Force (F) | F = m·a | F = m·a/gc = w·a/g | F = m·a | F = m·a | |
| Weight (w) | w = m·g | w = m·g/gc ≈ m | w = m·g | ||
| Units | |||||
| Acceleration (a) | ft/s2 | ft/s2 | ft/s2 | m/s2 | |
| Mass (m) | slug | pound-mass | pound | kilogram | |
| Force (F) | pound | pound-force | poundal | newton | |
See also
- Force gauge
- International System of Units (SI)
- Joule, SI unit of energy, 1 newton exerted over a distance of 1 metre
- Kilogram-force, force exerted by Earth's gravity at sea level on one kilogram of mass
- Pascal, SI unit of pressure, 1 newton acting on an area of 1 square metre
References
- ↑ "Table 3. Coherent derived units in the SI with special names and symbols". The International System of Units (SI). International Bureau of Weights and Measures. 2006. http://www.bipm.org/en/si/si_brochure/chapter2/2-2/table3.html.
- ↑ http://www.shakshienterprises.com/steel-fasteners.html#application1
- ↑ http://www.convertunits.com/from/kilonewtons/to/kilograms-force
|
||||||||||||||||||||
