Kepler's laws of planetary motion

In astronomy, Kepler's laws give an approximate description of the motion of planets around the Sun.
Kepler's laws are:
- The orbit of every planet is an ellipse with the Sun at one of the two foci.
- A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.[1]
- The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
Contents |
History
Johannes Kepler published his first two laws in 1609, having found them by analyzing the astronomical observations of Tycho Brahe.[2] Kepler did not discover his third law until many years later, and it was published in 1619.[2]
Almost a century later, Isaac Newton proved that relationships like Kepler's would apply exactly under certain ideal conditions approximately fulfilled in the solar system, as consequences of Newton's own laws of motion and law of universal gravitation.[3][4]
Because of the nonzero planetary masses and resulting perturbations, Kepler's laws apply only approximately and not exactly to the motions in the solar system.[3][5]
Voltaire's Eléments de la philosophie de Newton (Elements of Newton's Philosophy) was in 1738 the first publication to call Kepler's Laws "laws".[6]
Kepler's laws and his analysis of the observations on which they were based, the assertion that the Earth orbited the Sun, proof that the planets' speeds varied, and use of elliptical orbits rather than circular orbits with epicycles—challenged the long-accepted geocentric models of Aristotle and Ptolemy, and generally supported the heliocentric theory of Nicolaus Copernicus (although Kepler's ellipses likewise did away with Copernicus's circular orbits and epicycles).[2] Together with Newton's mathematical theories, they are part of the foundation of modern astronomy and physics. [3]
Generality
These laws approximately describe the motion of any two bodies in orbit around each other. (The statement in the first law about the focus becomes closer to exactitude as one of the masses becomes closer to zero mass. Where there are more than two masses, all of the statements in the laws become closer to exactitude as all except one of the masses become closer to zero mass and as the perturbations then also tend towards zero).[4] The masses of the two bodies can be nearly equal, e.g. Charon—Pluto (~1:10), in a small proportion, e.g. Moon—Earth (~1:100), or in a great proportion, e.g. Mercury—Sun (~1:10,000,000).
In all cases of two-body motion, rotation is about the barycenter of the two bodies, with neither one having its center of mass exactly at one focus of an ellipse. However, both orbits are ellipses with one focus at the barycenter. When the ratio of masses is large, the barycenter may be deep within the larger object, close to its center of mass. In such a case it may require sophisticated precision measurements to detect the separation of the barycenter from the center of mass of the larger object. But in the case of the planets orbiting the Sun, the largest of them are in mass as much as 1/1047.3486 (Jupiter) and 1/3497.898 (Saturn) of the solar mass,[7] and so it has long been known that the solar system barycenter can sometimes be outside the body of the Sun, up to about a solar diameter from its center.[8] Thus Kepler's first law, though not far off as an approximation, does not quite accurately describe the orbits of the planets around the Sun under classical physics.
Since Kepler stated his results with reference to the Sun and the planets, and did not know of their wider applicability, this article also discusses them with reference to the Sun and its planets.
At the time, Kepler's laws were radical claims; the prevailing belief (particularly in epicycle-based theories) was that orbits should be based on perfect circles. Kepler's observation was significant support for the Copernican view of the Universe, and still has relevance in a modern context. A circle is a form of ellipse, and most of the planets follow orbits of low eccentricity, which can be rather closely approximated as circles, so it is not immediately evident that the orbits are elliptical. Detailed calculations for the orbit of the planet Mars first indicated to Kepler its elliptical shape, and he inferred that other heavenly bodies, including those farther away from the Sun, have elliptical orbits too. That allows also for highly eccentric orbits (like very long stretched out circles). Bodies with highly eccentric orbits have been identified, among them the comets and many asteroids, discovered after Kepler's time. The dwarf planet Pluto was discovered as late as 1929, the delay mostly due to its small size, far distance, and optical faintness. Heavenly bodies such as comets with parabolic or even hyperbolic orbits are possible under the Newtonian theory and have been observed.[9]
To understand the second law let us suppose a planet takes one day to travel from point A to point B. The lines from the Sun to points A and B, together with the planet orbit, will define an (roughly triangular) area. This same area will be covered every day regardless of where in its orbit the planet is. Now as the first law states that the planet follows an ellipse, the planet is at different distances from the Sun at different parts in its orbit. So the planet has to move faster when it is closer to the Sun so that it sweeps an equal area.
Kepler's second law is equivalent to the fact that the force perpendicular to the radius vector is zero. The "areal velocity" is proportional to angular momentum, and so for the same reasons, Kepler's second law is also in effect a statement of the conservation of angular momentum.
The third law, published by Kepler in 1619 [1] captures the relationship between the distance of planets from the Sun, and their orbital periods. For example, suppose planet A is 4 times as far from the Sun as planet B. Then planet A must traverse 4 times the distance of Planet B each orbit, and moreover it turns out that planet A travels at half the speed of planet B, in order to maintain equilibrium with the reduced gravitational centripetal force due to being 4 times further from the Sun. In total it takes 4×2=8 times as long for planet A to travel an orbit, in agreement with the law (82=43).
This third law used to be known as the harmonic law,[10] because Kepler enunciated it in a laborious attempt to determine what he viewed as "the music of the spheres" according to precise laws, and express it in terms of musical notation.[11]
This third law currently receives additional attention as it can be used to estimate the distance from an exoplanet to its central star, and help to decide if this distance is inside the habitable zone of that star.[12].
Zero eccentricity
Kepler's laws refine upon the model of Copernicus. If the eccentricity of a planetary orbit is zero, then Kepler's laws state:
- The planetary orbit is a circle
- The Sun is in the center
- The speed of the planet in the orbit is constant
- The square of the sidereal period is proportionate to the cube of the distance from the Sun.
Actually the eccentricities of the orbits of the six planets known to Copernicus and Kepler are quite small, so this gives excellent approximations to the planetary motions, but Kepler's laws give even better fit to the observations.
Because the uniform circular motion was considered to be normal, a deviation from this motion was considered an anomaly. Kepler's corrections to the Copernican model are not at all obvious:
- The planetary orbit is not a circle, but an ellipse
- The Sun is not in the center but in a focal point
- Neither the linear speed nor the angular speed of the planet in the orbit is constant, but the area speed is constant.
- The square of the sidereal period is proportionate to the cube of the mean between the maximum and minimum distances from the Sun.
Estimating the eccentricity of earth orbit
The time from the March equinox to the September equinox is around 186 days, while the time from the September equinox to the March equinox is only around 179 days. This elementary observation shows that the eccentricity of the orbit of the earth is not exactly zero. The equator cuts the orbit into two parts having areas in the proportion 186 to 179, while a diameter cuts the orbit into equal parts. So the eccentricity of the orbit of the Earth is approximately
close to the correct value. (See Earth's orbit).
Nonzero planetary mass
Isaac Newton computed in his Philosophiæ Naturalis Principia Mathematica the acceleration of a planet moving according to Kepler's first and second law.
- The direction of the acceleration is towards the Sun.
- The magnitude of the acceleration is in inverse proportion to the square of the distance from the Sun.
This suggests that the Sun may be the physical cause of the acceleration of planets.
Newton defined the force on a planet to be the product of its mass and the acceleration. (See Newton's laws of motion). So:
- Every planet is attracted towards the Sun.
- The force on a planet is in direct proportion to the mass of the planet and in inverse proportion to the square of the distance from the Sun.
Here the Sun plays an unsymmetrical part which is unjustified. So he assumed Newton's law of universal gravitation:
- All bodies in the solar system attract one another.
- The force between two bodies is in direct proportion to their masses and in inverse proportion to the square of the distance between them.
As the planets have small masses compared to that of the Sun, the orbits conform to Kepler's laws approximately. Newton's model improves Kepler's model and gives better fit to the observations. See two-body problem.
The deviation of the motion of a planet from Kepler's laws due to attraction from other planets is called a perturbation.
Mathematics of the three laws
First law

Symbolically:
where (r, θ) are heliocentric polar coordinates for the planet, p is the semi-latus rectum, and ε is the eccentricity.
At θ = 0°, perihelion, the distance is minimum
At θ = 90°, the distance is 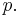
At θ = 180°, aphelion, the distance is maximum
The semi-major axis a is the arithmetic mean between rmin and rmax:
so
The semi-minor axis b is the geometric mean between rmin and rmax:
so
The semi-latus rectum p is the harmonic mean between rmin and rmax:
The eccentricity ε is the coefficient of variation between rmin and rmax:
The area of the ellipse is
The special case of a circle is ε = 0, resulting in r = p = rmin = rmax = a = b and A = π r2.
Second law

Symbolically:
where 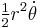 is the "areal velocity".
is the "areal velocity".
This is also known as the law of equal areas. It also applies for parabolic trajectories and hyperbolic trajectories.
Third law
- "The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit."
Symbolically:
where  is the orbital period of planet and
is the orbital period of planet and 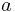 is the semimajor axis of the orbit.
is the semimajor axis of the orbit.
The proportionality constant is the same for any planet around the Sun.
So the constant is 1 (sidereal year)2(astronomical unit)−3 or 2.97472505×10−19 s2m−3. See the actual figures: attributes of major planets.
See also scaling in gravity.
Position as a function of time
Kepler used these three laws for computing the position of a planet as a function of time. His method involves the solution of a transcendental equation called Kepler's equation.
The procedure for calculating the heliocentric polar coordinates (r,θ) to a planetary position as a function of the time t since perihelion, and the orbital period P, is the following four steps.
- 1. Compute the mean anomaly M from the formula
- 2. Compute the eccentric anomaly E by solving Kepler's equation:
- 3. Compute the true anomaly θ by the equation:
- 4. Compute the heliocentric distance r from the first law:
The important special case of circular orbit, ε = 0, gives simply 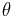 = E = M.
= E = M.
The proof of this procedure is shown below.
Mean anomaly
The Keplerian problem assumes an elliptical orbit and the four points:
- s the Sun (at one focus of ellipse);
- z the perihelion
- c the center of the ellipse
- p the planet
and
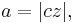 distance between center and perihelion, the semimajor axis,
distance between center and perihelion, the semimajor axis,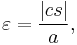 the eccentricity,
the eccentricity,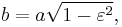 the semiminor axis,
the semiminor axis,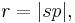 the distance between Sun and planet.
the distance between Sun and planet.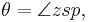 the direction to the planet as seen from the Sun, the true anomaly.
the direction to the planet as seen from the Sun, the true anomaly.
The problem is to compute the polar coordinates (r,θ) of the planet from the time since perihelion, t.
It is solved in steps. Kepler considered the circle with the major axis as a diameter, and
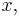 the projection of the planet to the auxiliary circle
the projection of the planet to the auxiliary circle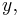 the point on the circle such that the sector areas |zcy| and |zsx| are equal,
the point on the circle such that the sector areas |zcy| and |zsx| are equal,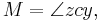 the mean anomaly.
the mean anomaly.
The sector areas are related by 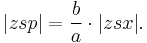
The circular sector area 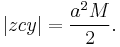
The area swept since perihelion,
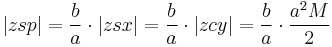
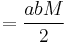 ,
,
is by Kepler's second law proportional to time since perihelion. So the mean anomaly, M, is proportional to time since perihelion, t.
where P is the orbital period.
Eccentric anomaly
When the mean anomaly M is computed, the goal is to compute the true anomaly θ. The function θ=f(M) is, however, not elementary. Kepler's solution is to use
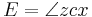 , x as seen from the centre, the eccentric anomaly
, x as seen from the centre, the eccentric anomaly
as an intermediate variable, and first compute E as a function of M by solving Kepler's equation below, and then compute the true anomaly θ from the eccentric anomaly E. Here are the details.
Division by a2/2 gives Kepler's equation
This equation gives M as a function of E. Determining E for a given M is the inverse problem. Iterative numerical algorithms are commonly used. Series are also used; they must be truncated, reducing accuracy.
Having computed the eccentric anomaly E, the next step is to calculate the true anomaly θ.
True anomaly
Note from the figure that
so that
Dividing by 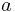 and inserting from Kepler's first law
and inserting from Kepler's first law
to get
The result is a usable relationship between the eccentric anomaly E and the true anomaly θ.
A computationally more convenient form follows by substituting into the trigonometric identity:
Get
Multiplying by (1+ε)/(1−ε) and taking the square root gives the result
We have now completed the third step in the connection between time and position in the orbit.
One could even develop a series computing θ directly from M. [2]
Distance
The fourth step is to compute the heliocentric distance r from the true anomaly θ by Kepler's first law:
Derivation from Newton's laws
Kepler's laws are concerned with the motion of the planets around the Sun. They are expressed as equations connecting the coordinates of the planet, and the time variable, with the parameters describing the position, size and shape of the orbit, the socalled orbital elements.
Newton's laws of motion are concerned with the motion of objects subject to impressed forces. Newton's law of universal gravitation specifies these forces. Together these laws constitute differential equations satisfied by planetary motions. Solving these equations constitute the n-body problem.
The solutions to the two-body problem, where there are only two particles involved, say, the sun and one planet, can be expressed analytically. These solutions include the elliptical Kepler orbits, but motions along other conic section (parabolas, hyperbolas and straight lines) also satisfy Newton's differential equations.
The solutions deviate from Kepler's laws in that
- the focus of the conic section is at the center of mass of the two bodies, rather than at the center of the Sun itself.
- the period of the orbit depends a little on the mass of the planet.
The language of Kepler's laws also applies when the motion of a planet is affected by the attraction from the other planets, as the orbits are described as Kepler orbits with slowly varying orbital elements. And in the case of the two-body problem in general relativity.
The derivations below involve the art of solving differential equations. The derivations below use heliocentric polar coordinates, see Figure 4. Kepler's second law is derived first, as the derivation of the first law depends on the derivation of the second law.
They can also be formulated and derived using Cartesian coordinates.[13][14]
Acceleration vector
From the heliocentric point of view consider the vector to the planet 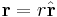 where
where  is the distance to the planet and the direction
is the distance to the planet and the direction  is a unit vector. When the planet moves the direction vector
is a unit vector. When the planet moves the direction vector  changes:
changes:
where 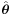 is the tangential (azimuthal) unit vector orthogonal to
is the tangential (azimuthal) unit vector orthogonal to 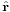 and pointing in the direction of rotation, and
and pointing in the direction of rotation, and  is the polar angle, and where a dot on top of the variable signifies differentiation with respect to time.
is the polar angle, and where a dot on top of the variable signifies differentiation with respect to time.
So differentiating the position vector twice to obtain the velocity and the acceleration vectors:
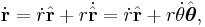
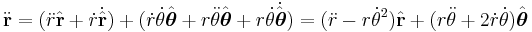 .
.
Note that for constant distance, 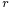 , the planet is subject to the centripetal acceleration,
, the planet is subject to the centripetal acceleration, 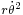 , and for constant angular speed,
, and for constant angular speed, 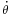 , the planet is subject to the Coriolis acceleration,
, the planet is subject to the Coriolis acceleration, 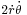 .
.
Equations of motion
Assume that the planet is so much lighter than the Sun that the acceleration of the Sun can be neglected.
Newton's law of gravitation says that "every object in the universe attracts every other object along a line of the centers of the objects, proportional to each object's mass, and inversely proportional to the square of the distance between the objects," and his second law of motion says that "the mass times the acceleration is equal to the force." So the mass of the planet ( ) times the acceleration vector of the planet (
) times the acceleration vector of the planet (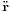 ) equals the mass of the Sun (
) equals the mass of the Sun (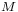 ) times the mass of the planet (
) times the mass of the planet ( ), divided by the square of the distance (
), divided by the square of the distance (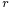 ), times minus the radial unit vector (
), times minus the radial unit vector (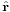 ), times a constant of proportionality (
), times a constant of proportionality (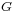 ). This is written:
). This is written:
Dividing by  and inserting the acceleration vector gives the vector equation of motion
and inserting the acceleration vector gives the vector equation of motion
Equating components, we get the two ordinary differential equations of motion, one for the acceleration in the 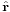 direction, the radial acceleration
direction, the radial acceleration
and one for the acceleration in the 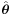 direction, the tangential or azimuthal acceleration:
direction, the tangential or azimuthal acceleration:
Deriving Kepler's second law
Only the tangential acceleration equation is needed to derive Kepler's second law.
The magnitude of the specific angular momentum
is a constant of motion, even if both the distance 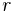 , and the angular speed
, and the angular speed 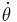 , and the tangential velocity
, and the tangential velocity 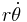 , vary, because
, vary, because
where the expression in the last parentheses vanishes due to the tangential acceleration equation.
The area swept out from time t1 to time t2,
depends only on the duration t2−t1. This is Kepler's second law.
Deriving Kepler's first law
To derive Kepler's first law, define:
where the constant
has the dimension of length. Then
and
Differentiation with respect to time is transformed into differentiation with respect to angle:
Differentiate
twice:
Substitute into the radial equation of motion
and get
Divide by the right hand side to get a simple non-homogeneous linear differential equation for the orbit of the planet:
An obvious solution to this equation is the circular orbit
Other solutions are obtained by adding solutions to the homogeneous linear differential equation with constant coefficients
These solutions are
where 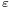 and
and 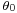 are arbitrary constants of integration. So the result is
are arbitrary constants of integration. So the result is
Choosing the axis of the coordinate system such that 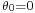 , and inserting
, and inserting 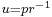 , gives:
, gives:
If 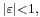 this is Kepler's first law.
this is Kepler's first law.
Deriving Kepler's third law
In the special case of circular orbits, which are ellipses with zero eccentricity, the relation between the radius a of the orbit and its period P can be derived relatively easily. The centripetal force of circular motion is proportional to a/P2, and it is provided by the gravitational force, which is proportional to 1/a2. Hence,
which is Kepler's third law for the special case.
In the general case of elliptical orbits, the derivation is more complicated.
The area of the planetary orbit ellipse is
The areal speed of the radius vector sweeping the orbit area is
where
The period of the orbit is
satisfying
implying Kepler's third law
See also
- Kepler orbit
- Kepler problem
- Kepler's equation
- Circular motion
- Gravity
- Two-body problem
- Free-fall time
- Laplace-Runge-Lenz vector
Notes
- ↑ 1.0 1.1 Bryant, Jeff; Pavlyk, Oleksandr. "Kepler's Second Law", Wolfram Demonstrations Project. Retrieved December 27, 2009.
- ↑ 2.0 2.1 2.2 Holton, Gerald James; Brush, Stephen G. (2001). Physics, the Human Adventure: From Copernicus to Einstein and Beyond (3rd paperback ed.). Piscataway, NJ: Rutgers University Press. pp. 40–41. ISBN 0-8135-2908-5. http://books.google.com/books?id=czaGZzR0XOUC&pg=PA40. Retrieved December 27, 2009.
- ↑ 3.0 3.1 3.2 See also G E Smith, "Newton's Philosophiae Naturalis Principia Mathematica", especially the section Historical context ... in The Stanford Encyclopedia of Philosophy (Winter 2008 Edition), Edward N. Zalta (ed.).
- ↑ 4.0 4.1 Newton's showing, in the 'Principia', that the two-body problem with centripetal forces results in motion in one of the conic sections, is concluded at Book 1, Proposition 13, Corollary 1. His consideration of the effects of perturbations in a multi-body situation starts at Book 1, Proposition 65, including a limit argument that the error in the (Keplerian) approximation of ellipses and equal areas would tend to zero if the relevant planetary masses would tend to zero and with them the planetary mutual perturbations (Proposition 65, Case 1). He discusses the extent of the perturbations in the real solar system in Book 3, Proposition 13.
- ↑ Kepler "for the first time revealed" a "real approximation to the true kinematical relations [motions] of the solar system", see page 1 in H C Plummer (1918), An introductory treatise on dynamical astronomy, Cambridge, 1918.
- ↑ Wilson, Curtis (May 1994). "Kepler's Laws, So-Called". HAD News (Washington, DC: Historical Astronomy Division, American Astronomical Society) (31): 1–2. http://had.aas.org/hadnews/HADN31.pdf. Retrieved December 27, 2009.
- ↑ Astronomical Almanac for 2008, page K7.
- ↑ The fact was already stated by Newton ('Principia', Book 3, Proposition 12).
- ↑ Dunbar, Brian (2008), SECCHI Makes a Fantastic Recovery!, NASA, http://erc.ivv.nasa.gov/mission_pages/stereo/news/SECCHI_P2003.html
- ↑ Gerald James Holton, Stephen G. Brush (2001). Physics, the Human Adventure. Rutgers University Press. p. 45. ISBN 0813529085. http://books.google.com/books?id=czaGZzR0XOUC&pg=PA45&dq=Kepler+%22harmonic+law%22&lr=&as_brr=0.
- ↑ Burtt, Edwin. The Metaphysical Foundations of Modern Physical Science. p. 52.
- ↑ http://www.astro.lsa.umich.edu/undergrad/Labs/extrasolar_planets/pn_intro.html
- ↑ Hyman, Andrew. "A Simple Cartesian Treatment of Planetary Motion", European Journal of Physics, Vol. 14, pp. 145–147 (1993).
- ↑ Further derivations are given in E T Whittaker, Analytical Dynamics (2nd edn. Cambridge, 1917), see pages 86 onwards.
References
- Kepler's life is summarized on pages 627–623 and Book Five of his magnum opus, Harmonice Mundi (harmonies of the world), is reprinted on pages 635–732 of On the Shoulders of Giants: The Great Works of Physics and Astronomy (works by Copernicus, Kepler, Galileo, Newton, and Einstein). Stephen Hawking, ed. 2002 ISBN 0-7624-1348-4
- A derivation of Kepler's third law of planetary motion is a standard topic in engineering mechanics classes. See, for example, pages 161–164 of Meriam, J. L. (1966, 1971), Dynamics, 2nd ed., New York: John Wiley, ISBN 0-471-59601-9.
- Murray and Dermott, Solar System Dynamics, Cambridge University Press 1999, ISBN 0-521-57597-4
External links
- B.Surendranath Reddy; animation of Kepler's laws: applet
- Crowell, Benjamin, Conservation Laws, http://www.lightandmatter.com/area1book2.html, an online book that gives a proof of the first law without the use of calculus. (see section 5.2, p. 112)
- David McNamara and Gianfranco Vidali, Kepler's Second Law - Java Interactive Tutorial, http://www.phy.syr.edu/courses/java/mc_html/kepler.html, an interactive Java applet that aids in the understanding of Kepler's Second Law.
- University of Tennessee's Dept. Physics & Astronomy: Astronomy 161 page on Johannes Kepler: The Laws of Planetary Motion [3]
- Equant compared to Kepler: interactive model [4]
- Kepler's Third Law:interactive model [5]
- Solar System Simulator (Interactive Applet)
|
||||||||||||||||||||||||||||||||||||||||||||||
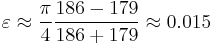
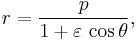
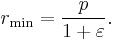
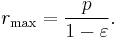
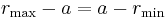
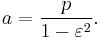
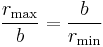
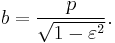
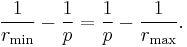
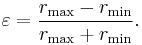
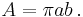
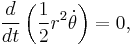
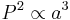
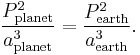
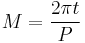
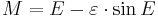
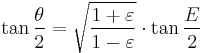
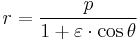
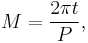

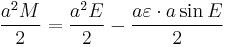
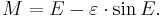
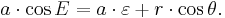
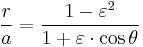
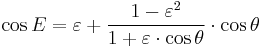
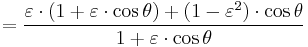
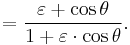
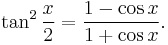
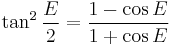
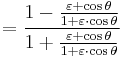
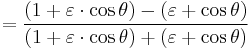
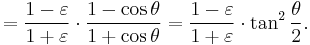
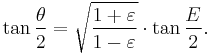
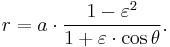
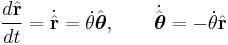
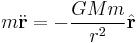
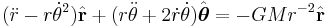
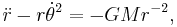
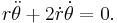
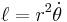
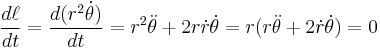
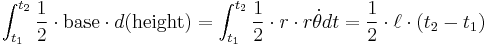
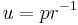
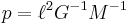
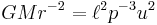
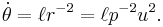
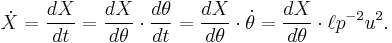
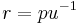
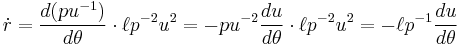
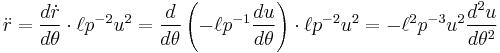
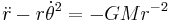
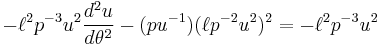
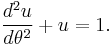
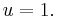
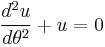
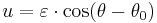
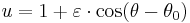
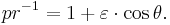
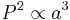
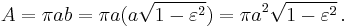
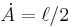
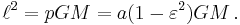
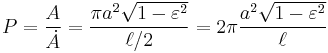
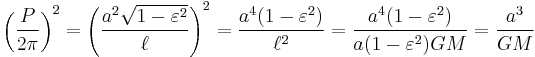
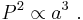




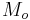
 True anomaly
True anomaly Semi-minor axis
Semi-minor axis
 Eccentric anomaly
Eccentric anomaly Mean longitude
Mean longitude True longitude
True longitude