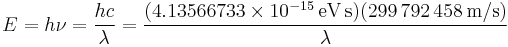Electronvolt
In physics, the electron volt (symbol eV; also written electronvolt[1][2]) is a unit of energy equal to approximately 1.602×10−19 J. By definition, it is equal to the amount of kinetic energy gained by a single unbound electron when it accelerates through an electric potential difference of one volt. Thus it is 1 volt (1 joule per coulomb) multiplied by the electron charge (1 e, or 1.60217653(14)×10−19 C). Therefore, one electron volt is equal to 1.60217653(14)×10−19 J.[3] Historically, the electron volt was devised as a standard unit of measure through its usefulness in electrostatic particle accelerator sciences because a particle with charge q has an energy E=qV after passing through the potential V; if q is quoted in integer units of the elementary charge and the terminal bias in volts, one gets an energy in eV.
The electron volt is not an SI unit and its value must be obtained experimentally.[4] It is a common unit of energy within physics, widely used in solid state, atomic, nuclear, and particle physics. It is commonly used with the SI prefixes milli-, kilo-, mega-, giga-, tera-, or peta- (meV, keV, MeV, GeV, TeV and PeV respectively). Thus meV stands for milli-electron volt.
In chemistry, it is often useful to have the molar equivalent, that is the kinetic energy that would be gained by one mole of electrons (6.02214179(30)×1023) passing through a potential difference of one volt. This is equal to 96.48534(2) kJ/mol. Atomic properties like the ionization energy are often quoted in electron volts.
Contents |
As a unit of energy
Conversion factors:
- 1 eV = 1.602176487(40)×10−19 J (the conversion factor is numerically equal to the elementary charge expressed in coulombs).
- 1 eV is 96.485 MJ/kmol.[5]
For comparison:
- ~624 EeV (600,000,000 TeV): energy needed to power a single 10 watt light bulb for one second. (100W = 100J/s = ~6.24x10^20 eV/s).
- 300 EeV (300,000 PeV) :[6] the so called Oh-My-God particle (the most energetic cosmic ray particle ever observed).
- 14 TeV: the design proton collision energy at the Large Hadron Collider (which has operated at half of the energy since March 30, 2010).
- 1 TeV: A trillion electronvolts, or 1.602×10−7 J, about the kinetic energy of a flying mosquito.[7]
- 210 MeV: The average energy released in fission of one Pu-239 atom.
- 200 MeV: The total energy released in nuclear fission of one U-235 atom (on average; depends on the precise break up).
- 17.6 MeV: The total energy released in the fusion of deuterium and tritium to form He-4 (also on average); this is 0.41 PJ per kilogram of product produced.
- 1 MeV: Or, 1.602×10−13 J, about twice the rest mass-energy of an electron.
- 13.6 eV: The energy required to ionize atomic hydrogen. Molecular bond energies are on the order of one eV per molecule.
- 1.3 to 2.1 eV: the photon energy of visible light.
- 1/40 eV: The thermal energy at room temperature. A single molecule in the air has an average kinetic energy 3/80 eV.
In some older documents, and in the name Bevatron, the symbol BeV is used, which stands for billion electron volts; it is equivalent to the GeV.
As a unit of momentum
In high-energy physics, the electronvolt is often used as a unit of momentum, in terms of GeV/c or TeV/c, which in natural units (c=1) are simply written GeV and TeV.
As a unit of mass
By mass-energy equivalence, the electron volt is also a unit of mass. It is common in particle physics, where mass and energy are often interchanged, to use eV/c2, where c is the speed of light in a vacuum (from E = mc2). Even more common is to use a system of natural units with c set to 1, and simply use eV as a unit of mass.
For example, an electron and a positron, each with a mass of 0.511 MeV/c2, can annihilate to yield 1.022 MeV of energy. The proton has a mass of 0.938 GeV/c2, making a gigaelectronvolt a very convenient unit of mass for particle physics.
-
- 1 GeV/c2 = 1.783 × 10−27 kg
The atomic mass unit, 1 gram divided by Avogadro's number, is almost the mass of a hydrogen atom, which is mostly the mass of the proton. To convert to megaelectronvolts, use the formula:
-
- 1 amu = 931.46 MeV/c2 = 0.93146 GeV/c2
- 1 MeV/c2 = 1.074 × 10–3 amu
Relation to units of time and distance
In particle physics, a system of units in which the speed of light in a vacuum c and the reduced Planck constant ħ are dimensionless and equal to unity is widely used: c = ħ = 1. In these units, both distances and times are expressed in inverse energy units (while energy and mass are expressed in the same units, see Mass–energy equivalence). In particular, particle scattering lengths are often presented in units of inverse particle masses.
Outside this system of units, the conversion factors between electronvolt, second, and nanometer are the following:[8]
The above relations also allow expressing the mean lifetime τ of an unstable particle (in seconds) in terms of its decay width Γ (in eV) via Γ = ħ/τ. For example, the B0 meson has a lifetime of 1.530(9) picoseconds, mean decay length is cτ = 459.7 µm, or a decay width of 4.302±25×10−4 eV.
Conversely, the tiny meson mass mass differences responsible for meson oscillations are often expressed in the more convenient inverse picoseconds.
As a unit of temperature
In certain fields, such as plasma physics, it is convenient to use the electronvolt as a unit of temperature. The conversion to kelvins (symbol: uppercase K) is defined by using kB, the Boltzmann constant:
For example, a typical magnetic confinement fusion plasma is 15 keV, or 170 megakelvins.
Photon properties


The energy E, frequency ν, and wavelength λ of a photon are related by
where h is Planck's constant, c is the speed of light. For quick calculations, this reduces to
A stream of photons with a wavelength of 532 nm (green light) would have an energy of approximately 2.33 eV. Similarly, 1 eV would correspond to a stream of infrared photons of wavelength 1240 nm, and so on.
1 eV = 8065.5447 cm-1
In scattering experiments
In a low-energy nuclear scattering experiment, it is conventional to refer to the nuclear recoil energy in units of eVr, keVr, etc. This distinguishes the nuclear recoil energy from the "electron equivalent" recoil energy (eVee, keVee, etc.) measured by scintillation light. For example, the yield of a phototube is measured in phe/keVee (photoelectrons per keV electron-equivalent energy). The relationship between eV, eVr, and eVee depends on the medium the scattering takes place in, and must be established empirically for each material.
See also
- Orders of magnitude (energy)
References
- ↑ IUPAC Gold Book, p. 75
- ↑ SI brochure, Sec. 4.1 Table 7
- ↑ P.J. Mohr, B.N. Taylor (2005). "CODATA recommended values of the fundamental physical constants: 2002". Reviews of Modern Physics 77: 1–107. doi:10.1103/RevModPhys.77.1. http://www.atomwave.org/rmparticle/ao%20refs/aifm%20refs%20sorted%20by%20topic/other%20rmp%20articles/CODATA2005.pdf. An in-depth discussion of how the CODATA constants were selected and determined.
- ↑ http://physics.nist.gov/cuu/Units/outside.html
- ↑ Atkins physical chemistry 9th edition
- ↑ Open Questions in Physics. German Electron-Synchrotron. A Research Centre of the Helmholtz Association. Updated March 2006 by JCB. Original by John Baez.
- ↑ CERN - Glossary
- ↑ C. Amsler et al. (2008). "Review of Particle Physics". Physics Letters B 667: 1. doi:10.1016/j.physletb.2008.07.018. http://pdg.lbl.gov/2008/reviews/consrpp.pdf.
External links
- BIPM's definition of the electronvolt
- http://physics.nist.gov/cuu/Constants physical constants reference; CODATA data