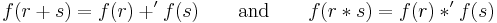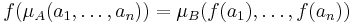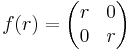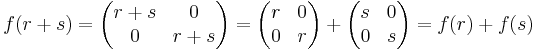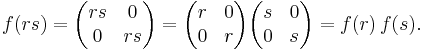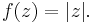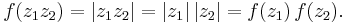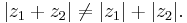Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures (such as groups, rings, or vector spaces). The word homomorphism comes from the Greek language: ὁμός (homos) meaning "same" and μορφή (morphe) meaning "shape".
Contents |
Definition and illustration
Definition
The definition of homomorphism depends on the type of algebraic structure under consideration. Particular definitions of homomorphism include the following:
- A group homomorphism is a homomorphism between two groups.
- A ring homomorphism is a homomorphism between two rings.
- A linear map is a homomorphism between two vector spaces.
- An algebra homomorphism is a homomorphism between two algebras.
- A functor is a homomorphism between two categories
The common theme is that a homomorphism is a function between two algebraic objects that respects the algebraic structure.
For example, a group is an algebraic object consisting of a set together with a single binary operation, satisfying certain axioms. If G and H are groups, a homomorphism from G to H is a function ƒ: G → H such that 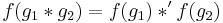 for any elements g1, g2 ∈ G, where * denotes the operation in G and *' denotes the operation in H.
for any elements g1, g2 ∈ G, where * denotes the operation in G and *' denotes the operation in H.
When an algebraic structure includes more than one operation, homomorphisms are required to preserve each operation. For example, a ring possesses both addition and multiplication, and a homomorphism between two rings is a function such that
for any elements r and s of the domain ring. In most contexts, a homomorphism will map identity elements to identity elements, inverse elements to inverse elements, and so forth.
The notion of a homomorphism can be given a formal definition in the context of universal algebra, a field which studies ideas common to all algebraic structures. In this setting, a homomorphism ƒ: A → B is a function between two algebraic structures of the same type such that
for each n-ary operation μ and for all elements a1,...,an ∈ A.
Basic examples
The real numbers are a ring, having both addition and multiplication. The set of all 2 × 2 matrices is also a ring, under matrix addition and matrix multiplication. If we define a function between these rings as follows:
where r is a real number. Then ƒ is a homomorphism of rings, since ƒ preserves both addition:
and multiplication:
For another example, the nonzero complex numbers form a group under the operation of multiplication, as do the nonzero real numbers. (Zero must be excluded from both groups since it does not have a multiplicative inverse, which is required for elements of a group.) Define a function ƒ from the nonzero complex numbers to the nonzero real numbers by
That is, ƒ(z) is the absolute value (or modulus) of the complex number z. Then ƒ is a homomorphism of groups, since it preserves multiplication:
Note that ƒ cannot be extended to a homomorphism of rings (from the complex numbers to the real numbers), since it does not preserve addition:
Informal discussion
Because abstract algebra studies sets endowed with operations that generate interesting structure or properties on the set, functions which preserve the operations are especially important. These functions are known as homomorphisms.
For example, consider the natural numbers with addition as the operation. A function which preserves addition should have this property: f(a + b) = f(a) + f(b). For example, f(x) = 3x is one such homomorphism, since f(a + b) = 3(a + b) = 3a + 3b = f(a) + f(b). Note that this homomorphism maps the natural numbers back into themselves.
Homomorphisms do not have to map between sets which have the same operations. For example, operation-preserving functions exist between the set of real numbers with addition and the set of positive real numbers with multiplication. A function which preserves operation should have this property: f(a + b) = f(a) * f(b), since addition is the operation in the first set and multiplication is the operation in the second. Given the laws of exponents, f(x) = ex satisfies this condition : 2 + 3 = 5 translates into e2 * e3 = e5.
A particularly important property of homomorphisms is that if an identity element is present, it is always preserved, that is, mapped to the identity. Note in the first example f(0) = 0, and 0 is the additive identity. In the second example, f(0) = 1, since 0 is the additive identity, and 1 is the multiplicative identity.
If we are considering multiple operations on a set, then all operations must be preserved for a function to be considered as a homomorphism. Even though the set may be the same, the same function might be a homomorphism, say, in group theory (sets with a single operation) but not in ring theory (sets with two related operations), because it fails to preserve the additional operation that ring theory considers.
Relation to category theory
Since homomorphisms are morphisms, the following specific kinds of morphisms defined in any category are defined for homomorphisms as well. However, the definitions in category theory are somewhat technical. In the important special case of module homomorphisms, and for some other classes of homomorphisms, there are much simpler descriptions, as follows:
- An isomorphism is a bijective homomorphism.
- An epimorphism (sometimes called a cover) is a surjective homomorphism.
- A monomorphism (sometimes called an embedding or extension) is an injective homomorphism.
- An endomorphism is a homomorphism from an object to itself.
- An automorphism is an endomorphism which is also an isomorphism.
These descriptions may be used in order to derive several interesting properties. For instance, since a function is bijective if and only if it is both injective and surjective, a module homomorphism is an isomorphism if and only if it is both a monomorphism and an epimorphism.
For endomorphisms and automorphisms, the descriptions above coincide with the category theoretic definitions; the first three descriptions do not. For instance, the precise definition for a homomorphism f to be iso is not only that it is bijective, and thus has an inverse f-1, but also that this inverse is a homomorphism, too. This has the important consequence that two objects are completely indistinguishable as far as the structure in question is concerned, if there is an isomorphism between them. Two such objects are said to be isomorphic.
Actually, in the algebraic setting (at least within the context of universal algebra) this extra condition on isomorphisms is automatically satisfied. However, the same is not true for epimorphisms; for instance, the inclusion of Z as a (unitary) subring of Q is not surjective, but an epimorphic ring homomorphism[1]. This inclusion thus also is an example of a ring homomorphism which is both mono and epi, but not iso.
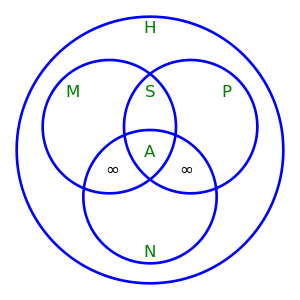
- Relationships between different kinds of module homomorphisms.
H = set of Homomorphisms, M = set of Monomorphisms,
P = set of ePimorphisms, S = set of iSomorphisms,
N = set of eNdomorphisms, A = set of Automorphisms.
Notice that: M ∩ P = S, S ∩ N = A,
(M ∩ N) \ A and (P ∩ N) \ A contain only homomorphisms from some infinite modules to themselves.
Kernel of a homomorphism
Any homomorphism f : X → Y defines an equivalence relation ~ on X by a ~ b if and only if f(a) = f(b). The relation ~ is called the kernel of f. It is a congruence relation on X. The quotient set X/~ can then be given an object-structure in a natural way, i.e. [x] * [y] = [x * y]. In that case the image of X in Y under the homomorphism f is necessarily isomorphic to X/~; this fact is one of the isomorphism theorems. Note in some cases (e.g. groups or rings), a single equivalence class K suffices to specify the structure of the quotient; so we can write it X/K. (X/K is usually read as "X mod K".) Also in these cases, it is K, rather than ~, that is called the kernel of f (cf. normal subgroup).
Homomorphisms of relational structures
In model theory, the notion of an algebraic structure is generalized to structures involving both operations and relations. Let L be a signature consisting of function and relation symbols, and A, B be two L-structures. Then a homomorphism from A to B is a mapping h from the domain of A to the domain of B such that
- h(FA(a1,…,an)) = FB(h(a1),…,h(an)) for each n-ary function symbol F in L,
- RA(a1,…,an) implies RB(h(a1),…,h(an)) for each n-ary relation symbol R in L.
In the special case with just one binary relation, we obtain the notion of a graph homomorphism.
Homomorphisms and e-free homomorphisms in formal language theory
Homomorphisms are also used in the study of formal languages.[2] Given alphabets 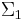 and
and 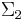 , a function h :
, a function h : 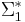 →
→ 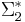 such that
such that 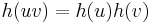 for all u and v in
for all u and v in 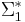 is called a homomorphism on
is called a homomorphism on 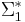 .[3] Let e denote the empty word. If h is a homomorphism on
.[3] Let e denote the empty word. If h is a homomorphism on 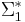 and
and 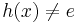 for all
for all 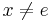 in
in 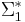 , then h is called an e-free homomorphism.
, then h is called an e-free homomorphism.
See also
- continuous function
- diffeomorphism
- homomorphic secret sharing – a simplistic decentralized voting protocol
- morphism
References
- ↑ Exercise 4 in section I.5, in Saunders Mac Lane, Categories for the Working Mathematician, ISBN 0-387-90036-5
- ↑ Seymour Ginsburg, Algebraic and automata theoretic properties of formal languages, North-Holland, 1975, ISBN 0 7204 2506 9.
- ↑ In homomorphisms on formal languages, the * operation is the Kleene star operation. The
 and
and 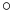 are both concatenation, commonly denoted by juxtaposition.
are both concatenation, commonly denoted by juxtaposition.
A monograph available free online:
- Burris, Stanley N., and H.P. Sankappanavar, H. P., 1981. A Course in Universal Algebra. Springer-Verlag. ISBN 3-540-90578-2.