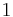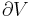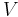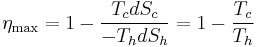Heat engine

Thermodynamics

Branches
Classical · Statistical · Chemical Equilibrium / Non-equilibrium Thermofluids

Laws
Zeroth · First · Second · Third

Systems
State: Equation of state Ideal gas · Real gas Phase of matter · Equilibrium Control volume · Instruments Processes: Isobaric · Isochoric · Isothermal Adiabatic · Isentropic · Isenthalpic Quasistatic · Polytropic Free expansion Reversibility · Irreversibility Endoreversibility Cycles: Heat engines · Heat pumps Thermal efficiency

System properties
Property diagrams Intensive and extensive properties State functions: Temperature / Entropy (intro.) † Pressure / Volume † Chemical potential / Particle no. † († Conjugate variables) Vapor quality Reduced properties Process functions: Work · Heat

Material properties

Specific heat capacity

$c=$

$T$	$\partial S$
$N$	$\partial T$

Compressibility

$\beta=-$

$1$	$\partial V$
$V$	$\partial p$

Thermal expansion

$\alpha=$

$1$	$\partial V$
$V$	$\partial T$

Property database

Equations
Carnot's theorem Clausius theorem Fundamental relation Ideal gas law Maxwell relations Table of thermodynamic equations

Potentials

Free energy · Free entropy

Internal energy	$U(S,V)$
Enthalpy	$H(S,p)=U+pV$
Helmholtz free energy	$A(T,V)=U-TS$
Gibbs free energy	$G(T,p)=H-TS$

History and culture

Philosophy:
Entropy and time · Entropy and life
Brownian ratchet
Maxwell's demon
Heat death paradox
Loschmidt's paradox
Synergetics

History:
General · Heat · Entropy · Gas laws
Perpetual motion
Theories:
Caloric theory · Vis viva
Theory of heat
Mechanical equivalent of heat
Motive power
Publications:
"An Experimental Enquiry Concerning ... Heat"
"On the Equilibrium of Heterogeneous Substances"
"Reflections on the
Motive Power of Fire"

Timelines of:
Thermodynamics · Heat engines

Art:
Maxwell's thermodynamic surface

Education:
Entropy as energy dispersal

Scientists
Daniel Bernoulli Sadi Carnot Benoît Paul Émile Clapeyron Rudolf Clausius Hermann von Helmholtz Julius Robert von Mayer William Rankine John Smeaton Georg Ernst Stahl Benjamin Thompson William Thomson John James Waterston

Overview

Figure 1: Heat engine diagram

Heat engines are often confused with the cycles they attempt to mimic. Typically when describing the physical device the term 'engine' is used. When describing the model the term 'cycle' is used.

In thermodynamics, heat engines are often modeled using a standard engineering model such as the Otto cycle. The theoretical model can be refined and augmented with actual data from an operating engine, using tools such as an indicator diagram. Since very few actual implementations of heat engines exactly match their underlying thermodynamic cycles, one could say that a thermodynamic cycle is an ideal case of a mechanical engine. In any case, fully understanding an engine and its efficiency requires gaining a good understanding of the (possibly simplified or idealized) theoretical model, the practical nuances of an actual mechanical engine, and the discrepancies between the two.

In general terms, the larger the difference in temperature between the hot source and the cold sink, the larger is the potential thermal efficiency of the cycle. On Earth, the cold side of any heat engine is limited to being close to the ambient temperature of the environment, or not much lower than 300 Kelvin, so most efforts to improve the thermodynamic efficiencies of various heat engines focus on increasing the temperature of the source, within material limits. The maximum theoretical efficiency of a heat engine (which no engine ever obtains) is equal to the temperature difference between the hot and cold ends divided by the temperature at the hot end, all expressed in absolute temperature or kelvins.

The efficiency of various heat engines proposed or used today ranges from 3 percent (97 percent waste heat) for the OTEC ocean power proposal through 25 percent for most automotive engines, to 45 percent for a supercritical coal plant, to about 60 percent for a steam-cooled combined cycle gas turbine.^[1]

All of these processes gain their efficiency (or lack thereof) due to the temperature drop across them.

Power

Heat engines can be characterized by their specific power, which is typically given in kilowatts per litre of engine displacement (in the U.S. also horsepower per cubic inch). The result offers an approximation of the peak-power output of an engine. This is not to be confused with fuel efficiency, since high-efficiency often requires a lean fuel-air ratio, and thus lower power density. A modern high-performance car engine makes in excess of 75 kW/L (1.65 hp/in³).

Everyday examples

Examples of everyday heat engines include the steam engine, the diesel engine, and the gasoline (petrol) engine in an automobile. A common toy that is also a heat engine is a drinking bird. Also the stirling engine is a heat engine. All of these familiar heat engines are powered by the expansion of heated gases. The general surroundings are the heat sink, providing relatively cool gases which, when heated, expand rapidly to drive the mechanical motion of the engine.

Examples of heat engines

It is important to note that although some cycles have a typical combustion location (internal external), they often can be implemented as the other combustion cycle. For example, John Ericsson developed an external heated engine running on a cycle very much like the earlier Diesel cycle. In addition, the externally heated engines can often be implemented in open or closed cycles.

What this boils down to is there are thermodynamic cycles and a large number of ways of implementing them with mechanical devices called engines.

Phase change cycles

In these cycles and engines, the working fluids are gases and liquids. The engine converts the working fluid from a gas to a liquid, from liquid to gas, or both, generating work from the fluid expansion or compression.

Rankine cycle (classical steam engine)
Regenerative cycle (steam engine more efficient than Rankine cycle)
Organic Rankine Cycle (Coolant changing phase in temperature ranges of ice and hot liquid water)
Vapor to liquid cycle (Drinking bird, Injector, Minto wheel)
Liquid to solid cycle (Frost heaving — water changing from ice to liquid and back again can lift rock up to 60 m.)
Solid to gas cycle (Dry ice cannon — Dry ice sublimes to gas.)

Gas only cycles

In these cycles and engines the working fluid is always a gas (i.e., there is no phase change):

Carnot cycle (Carnot heat engine)
Ericsson Cycle (Caloric Ship John Ericsson)
Stirling cycle (Stirling engine, thermoacoustic devices)
Internal combustion engine (ICE):
- Otto cycle (e.g. Gasoline/Petrol engine, high-speed diesel engine)
- Diesel cycle (e.g. low-speed diesel engine)
- Atkinson Cycle (Atkinson Engine)
- Brayton cycle or Joule cycle originally Ericsson Cycle (gas turbine)
- Lenoir cycle (e.g., pulse jet engine)
- Miller cycle

Liquid only cycles

In these cycles and engines the working fluid are always like liquid:

Stirling Cycle (Malone engine)
Heat Regenerative Cyclone

Electron cycles

Thermoelectric (Peltier-Seebeck effect)
Thermionic emission
Thermotunnel cooling

Magnetic cycles

Thermo-magnetic motor (Tesla)

Cycles used for refrigeration

A refrigerator is a heat pump: a heat engine in reverse. Work is used to create a heat differential. Many cycles can run in reverse to move heat from the cold side to the hot side, making the cold side cooler and the hot side hotter. Internal combustion engine versions of these cycles are, by their nature, not reversible.

Vapor-compression refrigeration
Stirling engine#Stirling cryocoolers
Gas-absorption refrigerator
Air cycle machine
Vuilleumier refrigeration

Evaporative Heat Engines

The Barton evaporation engine is a heat engine based on a cycle producing power and cooled moist air from the evaporation of water into hot dry air.

Efficiency

The efficiency of a heat engine relates how much useful work is output for a given amount of heat energy input.

From the laws of thermodynamics:

$dW \ = \ dQ_c \ - \ (-dQ_h)$

where

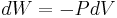$dW = -PdV$ is the work extracted from the engine. (It is negative since work is done by the engine.)

$dQ_h = T_hdS_h$ is the heat energy taken from the high temperature system. (It is negative since heat is extracted from the source, hence $(-dQ_h)$ is positive.)

$dQ_c = T_cdS_c$ is the heat energy delivered to the cold temperature system. (It is positive since heat is added to the sink.)

In other words, a heat engine absorbs heat energy from the high temperature heat source, converting part of it to useful work and delivering the rest to the cold temperature heat sink.

In general, the efficiency of a given heat transfer process (whether it be a refrigerator, a heat pump or an engine) is defined informally by the ratio of "what you get out" to "what you put in."

In the case of an engine, one desires to extract work and puts in a heat transfer.

$\eta = \frac{-dW}{-dQ_h} = \frac{-dQ_h - dQ_c}{-dQ_h} = 1 - \frac{dQ_c}{-dQ_h}$

The theoretical maximum efficiency of any heat engine depends only on the temperatures it operates between. This efficiency is usually derived using an ideal imaginary heat engine such as the Carnot heat engine, although other engines using different cycles can also attain maximum efficiency. Mathematically, this is because in reversible processes, the change in entropy of the cold reservoir is the negative of that of the hot reservoir (i.e., 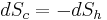$dS_c = -dS_h$ ), keeping the overall change of entropy zero. Thus:

$\eta_\text{max} = 1 - \frac{T_cdS_c}{-T_hdS_h} = 1 - \frac{T_c}{T_h}$

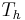where $T_h$ is the absolute temperature of the hot source and $T_c$ that of the cold sink, usually measured in kelvin. Note that $dS_c$ is positive while $dS_h$ is negative; in any reversible work-extracting process, entropy is overall not increased, but rather is moved from a hot (high-entropy) system to a cold (low-entropy one), decreasing the entropy of the heat source and increasing that of the heat sink.

The reasoning behind this being the maximal efficiency goes as follows. It is first assumed that if a more efficient heat engine than a Carnot engine is possible, then it could be driven in reverse as a heat pump. Mathematical analysis can be used to show that this assumed combination would result in a net decrease in entropy. Since, by the second law of thermodynamics, this is statistically improbable to the point of exclusion, the Carnot efficiency is a theoretical upper bound on the reliable efficiency of any process.

Empirically, no engine has ever been shown to run at a greater efficiency than a Carnot cycle heat engine.

Figure 2 and Figure 3 show variations on Carnot cycle efficiency. Figure 2 indicates how efficiency changes with an increase in the heat addition temperature for a constant compressor inlet temperature. Figure 3 indicates how the efficiency changes with an increase in the heat rejection temperature for a constant turbine inlet temperature.

Figure 2: Carnot cycle efficiency with changing heat addition temperature.

Figure 3: Carnot cycle efficiency with changing heat rejection temperature.

Endoreversible heat engines

The most ideal Carnot efficiency as a criterion of heat engine performance is the fact that by its nature, any maximally efficient Carnot cycle must operate at an infinitesimal temperature gradient. This is because any transfer of heat between two bodies at differing temperatures is irreversible, and therefore the Carnot efficiency expression only applies in the infinitesimal limit. The major problem with that is that the object of most heat engines is to output some sort of power, and infinitesimal power is usually not what is being sought.

A different measure of ideal heat engine efficiency is given by considerations of endoreversible thermodynamics, where the cycle is identical to the Carnot cycle except in that the two processes of heat transfer are not reversible (Callen 1985):

$\eta = 1 - \sqrt{\frac{T_c}{T_h}}$ (Note: Units K or °R)

This model does a better job of predicting how well real-world heat engines can do (Callen 1985, see also endoreversible thermodynamics):

**Efficiencies of Power Plants**
Power Plant	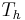$T_c$ (°C)	$T_h$ (°C)	$\eta$ (Carnot)	$\eta$ (Endoreversible)	$\eta$ (Observed)
West Thurrock (UK) coal-fired power plant	25	565	0.64	0.40	0.36
CANDU (Canada) nuclear power plant	25	300	0.48	0.28	0.30
Larderello (Italy) geothermal power plant	80	250	0.33	0.178	0.16

As shown, the endoreversible efficiency much more closely models the observed data.

History

Heat engines have been known since antiquity but were only made into useful devices at the time of the industrial revolution in the eighteenth century. They continue to be developed today.

Heat engine enhancements

Engineers have studied the various heat engine cycles extensively in an effort to improve the amount of usable work they could extract from a given power source. The Carnot Cycle limit cannot be reached with any gas-based cycle, but engineers have worked out at least two ways to possibly go around that limit, and one way to get better efficiency without bending any rules.

Increase the temperature difference in the heat engine. The simplest way to do this is to increase the hot side temperature, which is the approach used in modern combined-cycle gas turbines. Unfortunately, physical limits (such as the melting point of the materials from which the engine is constructed) and environmental concerns regarding NO_x production restrict the maximum temperature on workable heat engines. Modern gas turbines run at temperatures as high as possible within the range of temperatures necessary to maintain acceptable NO_x output . Another way of increasing efficiency is to lower the output temperature. One new method of doing so is to use mixed chemical working fluids, and then exploit the changing behavior of the mixtures. One of the most famous is the so-called Kalina cycle, which uses a 70/30 mix of ammonia and water as its working fluid. This mixture allows the cycle to generate useful power at considerably lower temperatures than most other processes.
Exploit the physical properties of the working fluid. The most common such exploitation is the use of water above the so-called critical point, or so-called supercritical steam. The behavior of fluids above their critical point changes radically, and with materials such as water and carbon dioxide it is possible to exploit those changes in behavior to extract greater thermodynamic efficiency from the heat engine, even if it is using a fairly conventional Brayton or Rankine cycle. A newer and very promising material for such applications is CO₂. SO₂ and xenon have also been considered for such applications, although SO₂ is a little toxic for most.
Exploit the chemical properties of the working fluid. A fairly new and novel exploit is to use exotic working fluids with advantageous chemical properties. One such is nitrogen dioxide (NO₂), a toxic component of smog, which has a natural dimer as di-nitrogen tetraoxide (N₂O₄). At low temperature, the N₂O₄ is compressed and then heated. The increasing temperature causes each N₂O₄ to break apart into two NO₂ molecules. This lowers the molecular weight of the working fluid, which drastically increases the efficiency of the cycle. Once the NO₂ has expanded through the turbine, it is cooled by the heat sink, which causes it to recombine into N₂O₄. This is then fed back to the compressor for another cycle. Such species as aluminium bromide (Al₂Br₆), NOCl, and Ga₂I₆ have all been investigated for such uses. To date, their drawbacks have not warranted their use, despite the efficiency gains that can be realized.^[2]

Heat engine processes

Cycle	Process 1-2 (Compression)	Process 2-3 (Heat Addition)	Process 3-4 (Expansion)	Process 4-1 (Heat Rejection)	Notes
Power cycles normally with external combustion - or heat pump cycles:
Bell Coleman	adiabatic	isobaric	adiabatic	isobaric	A reversed Brayton cycle
Brayton	adiabatic	isobaric	adiabatic	isobaric	Jet engines aka first Ericsson cycle from 1833
Carnot	isentropic	isothermal	isentropic	isothermal
Diesel	adiabatic	isobaric	adiabatic	isochoric
Ericsson	isothermal	isobaric	isothermal	isobaric	the second Ericsson cycle from 1853
Scuderi	adiabatic	variable pressure and volume	adiabatic	isochoric
Stirling	isothermal	isochoric	isothermal	isochoric
Stoddard	adiabatic	isobaric	adiabatic	isobaric
Power cycles normally with internal combustion:
Lenoir	isobaric	isochoric	adiabatic	isobaric	Pulse jets (Note: 3 of the 4 processes are different)
Otto	adiabatic	isochoric	adiabatic	isochoric	Gasoline / petrol engines
Brayton	adiabatic	isobaric	adiabatic	isobaric	Steam engine

Each process is one of the following:

isothermal (at constant temperature, maintained with heat added or removed from a heat source or sink)
isobaric (at constant pressure)
isometric/isochoric (at constant volume), also referred to as iso-volumetric
adiabatic (no heat is added or removed from the system during adiabatic process which is equivalent to saying that the entropy remains constant)

References

↑ "Efficiency by the Numbers" by Lee S. Langston
↑ Nuclear Reactors Concepts and Thermodynamic Cycles

Notes

Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed. ed.). W. H. Freeman Company. ISBN 0-7167-1088-9.
Callen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics (2nd ed. ed.). John Wiley & Sons, Inc.. ISBN 0-471-86256-8.
On line museum of toy steam engines, including a very rare Bing heat engine

External links

Video of Stirling engine running on dry ice
Heat Engine
On line museum of toy steam engines, including a very rare Bing heat engine
Webarchive backup: Refrigeration Cycle Citat: "...The refrigeration cycle is basically the Rankine cycle run in reverse..."
Red Rock Energy Solar Heliostats: Heat Engine Projects Citat: "...Choosing a Heat Engine..."
Overview of heat engine types - not working
The rotary piston array machine
The gyroscope combustion motor
The external combustion air engine
Super-efficient Atkinson-Diesel Cycle

Thermodynamic cycles

External combustion cycles

Without phase change (Hot air engines)	Barton · Bell Coleman · Brayton/Joule (externally heated) · Carnot · Ericsson · Ported constant volume[1] · Stirling · Stirling (Pseudo / Adiabatic) · Stoddard

With phase change	Kalina · Rankine (Organic Rankine) · Regenerative · Two-phased Stirling[2]

Internal combustion cycles

Atkinson · Brayton/Joule · Diesel · Expander · Gas-generator · Homogeneous Charge Compression Ignition · Lenoir · Miller · Otto · Pressure-fed · Staged combustion

Mixed cycles

Combined · HEHC · Mixed/Dual

Refrigeration cycles

Hampson-Linde · Kleemenko · Linde dual-pressure · Pulse tube · Regenerative cooling · Transcritical · Vapor absorption · Vapor-compression · Siemens · Vuilleumier

Uncategorized

Claude [3] · Claude dual-pressure · Fickett-Jacobs · Gifford-McMahon [4] · Hirn · Humphrey · Heylandt · Scuderi

Heat engines

Carnot engine · Free-piston · Fluidyne · Gas turbine · Hot air · Iris · Jet · Photo-Carnot engine · Piston · Pistonless (Rotary) · Rijke tube · Rocket · Split-single · Steam (reciprocating) · Steam turbine · Stirling · Swing-piston · Thermoacoustic

Beale number · West number

Timeline of heat engine technology

Thermodynamic cycle