Googolplex
A googolplex is the number 10googol, i.e. 1010100, which can also be written as the number 1 followed by a googol zeros (i.e. 10100 zeros).
Contents |
History
In 1938, Edward Kasner's nine-year-old nephew, Milton Sirotta, coined the term googol, then proposed the further term googolplex to be "one, followed by writing zeroes until you get tired". Kasner decided to adopt a more formal definition "because different people get tired at different times and it would never do to have Carnera be a better mathematician than Dr. Einstein, simply because he had more endurance and could write for longer".[1] It thus became standardized to 10googol.
Size
In the PBS science program Cosmos: A Personal Voyage, Episode 9: "The Lives of the Stars", astronomer and television personality Carl Sagan estimated that writing a googolplex in numerals (i.e., "10,000,000,000...") would be physically impossible, since doing so would require more space than the known universe provides.
An average book of 60 cubic inches can be printed with 5 × 105 zeroes (5 characters per word, 10 words per line, 25 lines per page, 400 pages), or 8.3 × 103 '0's per cubic inch. The observable (i.e. past light cone) universe contains 6 × 1083 cubic inches (1.3 × π × (14 × 109 light year in inches)3). This implies that if the universe is stuffed with paper printed with '0's, it could contain only 5.3 × 1087 '0's—far short of a googol of '0's. In fact there are only about 2.5 × 1089 elementary particles in the observable universe so even if one were to use an elementary particle to represent each digit, one still would require the universe's volume about a trillion times larger. Therefore a googolplex cannot be written out since a googol of '0's cannot fit into the observable universe.
The time it would take to write such a number also renders the task implausible: if a person can write two digits per second, it would take around about 1.51 × 1092 years, which is 1.1 × 1082 times the age of the universe, to write a googolplex.[2]
Consider printing the digits of a googolplex in unreadable, one-point font (0.353 mm per digit). It would take about 3.5 × 1096 metres to write a googolplex in one-point font. The observable universe is estimated to be 8.80 × 1026 meters, or 93 billion light-years, in diameter,[3] so the distance required to write the necessary zeroes is longer than the estimated universe.
One googol is also presumed to be greater than the number of hydrogen atoms in the observable universe, which has been variously estimated to be between 1079 and 1081.[4] A googol is also greater than the number of Planck times elapsed since the Big Bang, which is estimated at about 8 × 1060.
Thus in the physical world it is difficult to give examples of numbers that compare closely to a googolplex. In analyzing quantum states and black holes, physicist Don Page writes that "determining experimentally whether or not information is lost down black holes of solar mass ... would require more than 101076.96 measurements to give a rough determination of the final density matrix after a black hole evaporates".[5] The end of the Universe via Big Freeze without proton decay is subject to be 101076 years into the future, which is still short of googolplex.
In a separate article, Page shows that the number of states in a black hole with a mass roughly equivalent to the Andromeda Galaxy is in the range of a googolplex.[2]
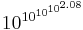(~ googolplex
) years—scale of an estimated Poincaré recurrence time for the quantum state of a hypothetical box containing a black hole with the mass within the presently visible region of our universe.[6] This time assumes a statistical model subject to Poincaré recurrence. A much simplified way of thinking about this time is in a model where our universe's history repeats itself arbitrarily many times due to properties of statistical mechanics, this is the time scale when it will first be somewhat similar (for a reasonable choice of "similar") to its current state again.
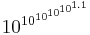(~ googolplex
) years—scale of an estimated Poincaré recurrence time for the quantum state of a hypothetical box containing a black hole with the estimated mass of the entire universe, observable or not, assuming a certain inflationary model with an inflaton whose mass is 10−6 Planck masses.[6]
In pure mathematics, the magnitude of a googolplex could be related to other forms of large number notation such as tetration, Knuth's up-arrow notation, Steinhaus-Moser notation, or Conway chained arrow notation.
Some sequences grow very quickly; for instance, the first two Ackermann numbers are 1 and 22 = 4; but then the third is 333, a power tower of threes more than seven trillion high.
Graham's number is vastly larger than a googolplex.
Other uses in popular culture
- The "Googleplex" is the Google company headquarters, located at 1600 Amphitheatre Parkway in Mountain View, Santa Clara County, California, near San Jose.
See also
- Large numbers
- Names of large numbers
References
- ↑ Kasner, Edward (2001). Mathematics and the imagination. Mineola, NY: Dover Publications.
- ↑ 2.0 2.1 Page, Don, "How to Get a Googolplex", 3 June 2001.
- ↑ Lineweaver, Charles; Tamara M. Davis (2005). "Misconceptions about the Big Bang". Scientific American. http://www.sciam.com/article.cfm?id=misconceptions-about-the-2005-03&page=5. Retrieved 2008-11-06.
- ↑ Mass, Size, and Density of the Universe Article from National Solar Observatory, 21 May 2001.
- ↑ Page, Don N., "Information Loss in Black Holes and/or Conscious Beings?", 25 Nov. 1994, for publication in Heat Kernel Techniques and Quantum Gravity, S. A. Fulling, ed. (Discourses in Mathematics and Its Applications, No. 4, Texas A&M University, Department of Mathematics, College Station, Texas, 1995)
- ↑ 6.0 6.1 Information Loss in Black Holes and/or Conscious Beings?, Don N. Page, Heat Kernel Techniques and Quantum Gravity (1995), S. A. Fulling (ed), p. 461. Discourses in Mathematics and its Applications, No. 4, Texas A&M University Department of Mathematics. arXiv:hep-th/9411193. ISBN 0963072838.
External links
- Weisstein, Eric W., "Googolplex" from MathWorld.
- googolplex at PlanetMath.
|
|||||||||||||||||||