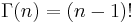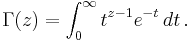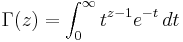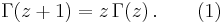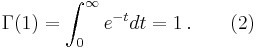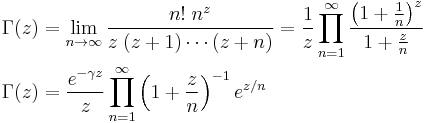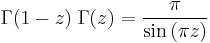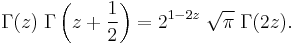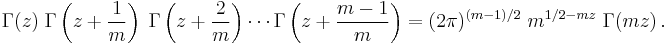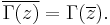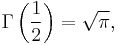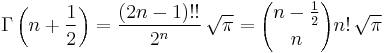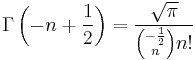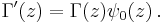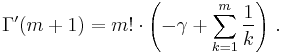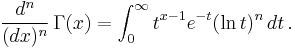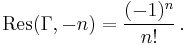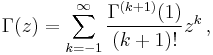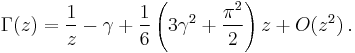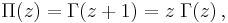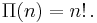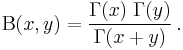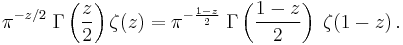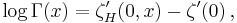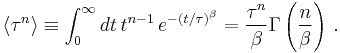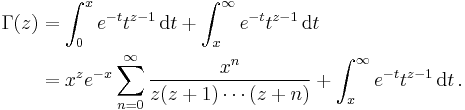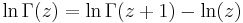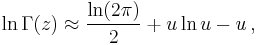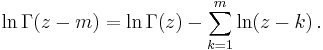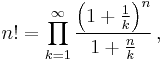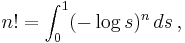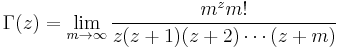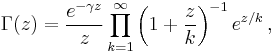Gamma function

The Gamma function along part of the real axis

In mathematics, the Gamma function (represented by the capital Greek letter Γ) is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers.

If n is a positive integer, then

$\Gamma(n) = (n-1)!\,$

showing the connection to the factorial function.

Although the Gamma function is defined for all complex numbers except the non-positive integers, it is defined via an integral that converges only for complex numbers with a positive real part. When z is a complex number with a positive real part, the Gamma function is

$\Gamma(z) = \int_0^\infty t^{z-1} e^{-t}\,dt\,.$

This definition is extended by analytic continuation to all complex numbers except the non-positive integers. Thus, the Gamma function extends the factorial function to (almost all) real and complex values of n.

The Gamma function is a component in various probability-distribution functions, and as such it is applicable in the fields of probability and statistics, as well as combinatorics.

1 Motivation
2 Definition
- 2.1 Main definition
- 2.2 Alternative definitions
3 Properties
4 Approximations
5 History
6 See also
7 Notes
8 References
9 External links

Motivation

It is easy to graphically interpolate the factorial function to non-integer values, but is there a formula that describes the resulting curve?

The gamma function can be seen as a solution to the following interpolation problem:

"Find a smooth curve that connects the points (x, y) given by y = (x − 1)! at the positive integer values for x."

A plot of the first few factorials makes clear that such a curve can be drawn, but it would be preferable to have a formula that precisely describes the curve, in which the number of operations does not depend on the size of n. The formula for the factorial, n!, cannot be used directly for fractional values of n since it is only valid when n is an integer. There is, in fact, no such simple solution for factorials; any combination of sums, products, powers, exponential functions, or logarithms with a fixed number of terms will not suffice to express n!. However, it is possible to find a general formula for factorials using tools such as integrals and limits from calculus. A good solution to this is the gamma function.

There are infinitely many continuous extensions of the factorial to non-integers: infinitely many curves can be drawn through any set of isolated points. The gamma function is the most useful solution in practice, is analytic (except at the non-positive integers), and can be characterized in several ways. However, it is not the only analytic function which extends the factorial, as adding to it any analytic function which is zero on the positive integers will give another function with that property.

Definition

Main definition

The extended version of the Gamma function in the complex plane

The notation $\Gamma(z)$ is due to Legendre. If the real part of the complex number z is positive (Re(z) > 0), then the integral

$\Gamma(z) = \int_0^\infty t^{z-1} e^{-t}\,dt$

converges absolutely. Using integration by parts, one can show that

$\Gamma(z+1)=z \, \Gamma(z)\,. \qquad \text{(1)}$

This functional equation is similar to the property n! = n · (n − 1)! of the factorial function. But also, evaluating Γ(1) we get:

$\Gamma(1) = \int_0^\infty e^{-t} dt = 1\,. \qquad\text{(2)}$

Combining these two results it follows by induction that the factorial function is a translation of a special case of the Gamma function:

$\Gamma(n) = (n-1)!\,$

for all positive integers n.

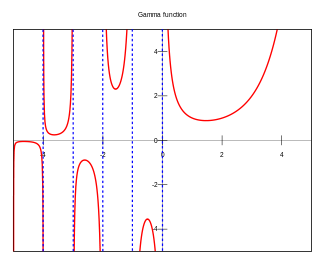
The absolute value of the Gamma function on the complex plane.

The identity Γ(z) = Γ(z+1) / z can be used (or, yielding the same result, analytic continuation can be used) to extend the integral formulation for Γ(z) to a meromorphic function defined for all complex numbers z, except z = −n for integers n ≥ 0, where the function has simple poles with residue (−1)ⁿ/n!.

It is this extended version that is commonly referred to as the gamma function.

Alternative definitions

The following infinite product definitions for the Gamma function, due to Euler and Weierstrass respectively, are valid for all complex numbers z, except the non-positive integers:

$\begin{align} \Gamma(z) &= \lim_{n \to \infty} \frac{n! \; n^z}{z \; (z+1)\cdots(z+n)} = \frac{1}{z} \prod_{n=1}^\infty \frac{\left(1+\frac{1}{n}\right)^z}{1+\frac{z}{n}} \\ \Gamma(z) &= \frac{e^{-\gamma z}}{z} \prod_{n=1}^\infty \left(1 + \frac{z}{n}\right)^{-1} e^{z/n} \end{align}$

where γ ≈ 0.577216 is the Euler–Mascheroni constant.

It is straightforward to show that the Euler definition satisfies the functional equation (1) above.

A somewhat curious parametrization of the Gamma function is given in terms of Laguerre polynomials,

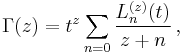$\Gamma(z)=t^z \sum_{n=0} \frac{L_n^{(z)}(t)}{z+n}\,,$ which converges for Re(z) < 1/2.

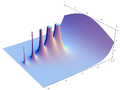Absolute value

Real part

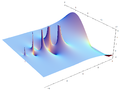Imaginary part

Properties

General

Other important functional equations for the Gamma function are Euler's reflection formula

$\Gamma(1-z) \; \Gamma(z) = {\pi \over \sin{(\pi z)}} \,$

and the duplication formula

$\Gamma(z) \; \Gamma\left(z + \frac{1}{2}\right) = 2^{1-2z} \; \sqrt{\pi} \; \Gamma(2z). \,$

The duplication formula is a special case of the multiplication theorem

$\Gamma(z) \; \Gamma\left(z + \frac{1}{m}\right) \; \Gamma\left(z + \frac{2}{m}\right) \cdots \Gamma\left(z + \frac{m-1}{m}\right) = (2 \pi)^{(m-1)/2} \; m^{1/2 - mz} \; \Gamma(mz)\,.$

A basic but useful property, which can be seen from the limit definition, is:

$\overline{\Gamma(z)} = \Gamma(\overline{z}). \,\!$

Perhaps the best-known value of the Gamma function at a non-integer argument is

$\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}, \,\!$

which can be found by setting z = 1/2 in the reflection or duplication formulas, by using the relation to the Beta function given below with x = y = 1/2, or simply by making the substitution 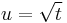$u = \sqrt{t}$ in the integral definition of the Gamma function, resulting in a Gaussian integral. In general, for integer values of n we have:

$\Gamma\left(n+\frac{1}{2}\right)= \frac{(2n-1)!!}{2^n}\, \sqrt{\pi} = {n-\frac{1}{2}\choose n} n! \, \sqrt{\pi}$

$\Gamma\left(-n+\frac{1}{2}\right)= \frac{\sqrt{\pi}}{{-\frac{1}{2} \choose n}n!}$

where n!! denotes the double factorial.

The derivatives of the Gamma function are described in terms of the polygamma function. For example:

$\Gamma'(z)=\Gamma(z)\psi_0(z)\,.$

For positive integer m the derivative of Gamma function can be calculated as follows (here γ is the Euler–Mascheroni constant):

$\Gamma'(m+1) = m!\cdot\left( - \gamma + \sum_{k=1}^m\frac{1}{k} \right)\,.$

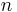The $n$ -th derivative of the Gamma function is:

${d^{n} \over (dx)^{n}}\,\Gamma(x) = \int_0^\infty t^{x-1} e^{-t} (\ln t)^{n} \,dt\,.$

This can be derived by differentiating the integral form of the Gamma function with respect to x, and using the technique of differentiation under the integral sign.

The Gamma function has simple poles at z = −n = 0, −1, −2, −3, ... . The residue there is

$\operatorname{Res}(\Gamma,-n)=\frac{(-1)^n}{n!}\,.$

Moreover, the Gamma function has the following Laurent expansion in 0

$\Gamma(z) = \sum_{k=-1}^\infty\frac{\Gamma^{(k+1)}(1)}{(k+1)!}z^{k}\,,$

valid for |z|<1. In particular

$\Gamma(z) = \frac1z-\gamma+\frac16\left(3\gamma^2+\frac {\pi^2}2\right)z+O(z^2)\,.$

The Bohr–Mollerup theorem states that among all functions extending the factorial functions to the positive real numbers, only the Gamma function is log-convex, that is, its natural logarithm is convex.

Pi function

An alternative notation which was originally introduced by Gauss and which was sometimes used is the Pi function, which in terms of the Gamma function is

$\Pi(z) = \Gamma(z+1) = z \; \Gamma(z)\,,$

so that

$\Pi(n) = n!\,.$

Relation to other functions

In the first integral above, which defines the Gamma function, the limits of integration are fixed. The upper and lower incomplete Gamma functions are the functions obtained by allowing the lower or upper (respectively) limit of integration to vary.
The Gamma function is related to the Beta function by the formula

$\Beta(x,y)=\frac{\Gamma(x) \; \Gamma(y)}{\Gamma(x+y)}\,.$

The derivative of the logarithm of the Gamma function is called the digamma function; higher derivatives are the polygamma functions.
The analog of the Gamma function over a finite field or a finite ring is the Gaussian sums, a type of exponential sum.
The reciprocal Gamma function is an entire function and has been studied as a specific topic.
The Gamma function also shows up in an important relation with the Riemann zeta function, ζ(z).

$\pi^{-z/2} \; \Gamma\left(\frac{z}{2}\right) \zeta(z) = \pi^{-\frac{1-z}{2}} \; \Gamma\left(\frac{1-z}{2}\right) \; \zeta(1-z)\,.$

And also in the following elegant formula:

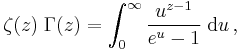$\zeta(z) \; \Gamma(z) = \int_{0}^{\infty} \frac{u^{z-1}}{e^u - 1} \; \mathrm{d}u\,,$ which is valid only for Re(z) > 1.

The logarithm of the Gamma function satisfies the following formula due to Lerch:

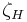$\log\Gamma(x) = \zeta_{H}'(0,x) - \zeta'(0)\,,$

where $\zeta_{H}$ is the Hurwitz zeta function, $\zeta$ is the Riemann zeta function and the prime (') denotes differentiation in the first variable.

The Gamma function is intimately related to the stretched exponential function. For instance, the moments of that function are

$\langle\tau^n\rangle \equiv \int_0^\infty dt\, t^{n-1}\, e^{ - \left( {t /\tau } \right)^\beta } = {\tau^n \over \beta }\Gamma \left({n \over \beta }\right)\,.$

Approximations

Complex values of the Gamma function can be computed numerically with arbitrary precision using Stirling's approximation or the Lanczos approximation.

The Gamma function can be computed to fixed precision for Re(z) ∈ [1, 2] by applying integration by parts to Euler's integral. For any positive number x the Gamma function can be written

$\begin{align}\Gamma(z) &= \int_0^x e^{-t} t^{z-1}\, \mathrm{d}t + \int_x^\infty e^{-t} t^{z-1}\, \mathrm{d}t \\&= x^z e^{-x} \sum_{n=0}^\infty \frac{x^n}{z(z+1) \cdots (z+n)} + \int_x^\infty e^{-t} t^{z-1}\, \mathrm{d}t \,.\end{align}$

When Re(z) ∈ [1, 2] and x ≥ 1, the absolute value of the last integral is smaller than (x + 1) e^−x. By choosing x large enough, this last expression can be made smaller than 2^−N for any desired value N. Thus, the Gamma function can be evaluated to N bits of precision with the above series. When z is rational, the computation can be performed with binary splitting in time O((log N)² M(N)) where M(N) is the time needed to multiply two N-bit numbers.

For arguments that are integer multiples of 1/24 the Gamma function can also be evaluated quickly using arithmetic-geometric mean iterations (see particular values of the Gamma function).

Because the Gamma and factorial functions grow so rapidly for moderately-large arguments, many computing environments include a function that returns the natural logarithm of the Gamma function (often given the name lngamma in programming environments or gammaln in spreadsheets); this grows much more slowly, and for combinatorial calculations allows adding and subtracting logs instead of multiplying and dividing very large values. The digamma function, which is the derivative of this function, is also commonly seen. In the context of technical and physical applications, e.g. with wave propagation, the functional equation

$\ln \Gamma(z) = \ln \Gamma(z+1) - \ln(z) \,$

is often used since it allows one to determine function values in one strip of width 1 in z from the neighbouring strip. In particular, starting with a good approximation for a z with large real part one may go step by step down to the desired z. Following an indication of Carl Friedrich Gauss Rocktaeschel (1922) proposes for lngamma an approximation for large Re(z):

$\ln\Gamma(z) \approx \frac{\ln(2\pi)}{2} + u \ln u - u\,,$

with u = z − 1/2. This can be used to accurately approximate 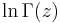$\ln\Gamma(z)$ for z with a smaller Re(z) via (P.E.Böhmer, 1939)

$\ln\Gamma(z-m) = \ln\Gamma(z) - \sum_{k=1}^{m} \ln(z-k)\,.$

A more accurate approximation can be obtained by using more terms from the asymptotic expansions of 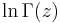$\ln \Gamma(z)$ and $\Gamma(z)$ , which are based on Stirling's approximation.

History

The gamma function has caught the interest of some of the most prominent mathematicians of all time. Its history, notably documented by Philip J. Davis in an article that won him the 1963 Chauvenet Prize, reflects many of the major developments within mathematics since the 18th century. In the words of Davis, "each generation has found something of interest to say about the gamma function. Perhaps the next generation will also."^[1]

18th century: Euler and Stirling

The first page of Euler's paper "De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt".

The problem of extending the factorial to non-integer arguments was apparently first considered by Daniel Bernoulli and Christian Goldbach in the 1720s, and was solved at the end of the same decade by Leonhard Euler. Euler gave two different definitions: the first was not his integral but an infinite product,

$n! = \prod_{k=1}^\infty \frac{\left(1+\frac{1}{k}\right)^n}{1+\frac{n}{k}}\,,$

of which he informed Goldbach in a letter dated October 13, 1729. He wrote to Goldbach again on January 8, 1730, to announce his discovery of the integral representation

$n!=\int_{0}^{1}(-\log s)^{n}\, ds\,,$

which is valid for n > 0. By the change of variables t = −log s, this becomes the familiar Euler integral. Euler published his results in the paper "De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt" ("On transcendental progressions, that is, those whose general terms cannot be given algebraically"), submitted to the St. Petersburg Academy on November 28, 1729.^[2] Euler further discovered some of the gamma function's important functional properties, including the reflection formula.

James Stirling, a contemporary of Euler, also attempted to find a continuous expression for the factorial and came up with what is now known as Stirling's formula. Although Stirling's formula gives a good estimate of 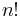$n!$ , also for non-integers, it does not provide the exact value. Extensions of his formula that correct the error were given by Stirling himself and by Jacques Philippe Marie Binet.

19th century: Gauss, Weierstrass and Legendre

Carl Friedrich Gauss rewrote Euler's product as

$\Gamma(z) = \lim_{m\to\infty}\frac{m^{z}m!}{z(z+1)(z+2)\cdots(z+m)}$

and used this formula to discover new properties of the gamma function. Although Euler was a pioneer in the theory of complex variables, he does not appear to have considered the factorial of a complex number, as instead Gauss first did.^[3] Gauss also proved the multiplication theorem of the gamma function and investigated the connection between the gamma function and elliptic integrals.

Karl Weierstrass further established the role of the gamma function in complex analysis, starting from yet another product representation,

$\Gamma(z) = \frac{e^{-\gamma z}}{z} \prod_{k=1}^\infty \left(1 + \frac{z}{k}\right)^{-1} e^{z/k}\,,$

where γ is the Euler–Mascheroni constant. Weierstrass originally wrote his product as one for 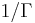$1/\Gamma$ , in which case it is taken over the function's zeros rather than its poles. Inspired by this result, he proved what is known as the Weierstrass factorization theorem — that any entire function can be written as a product over its zeros in the complex plane; a generalization of the fundamental theorem of algebra.

The name gamma function and the symbol $\Gamma$ were introduced by Adrien-Marie Legendre around 1811; Legendre also rewrote Euler's integral definition in its modern form. Although the symbol is an upper-case Greek Gamma, there is no accepted standard for whether the function name should be written "Gamma function" or "gamma function" (some authors simply write " $\Gamma$ -function"). 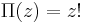The alternative "Pi function" notation $\Pi(z)=z!$ due to Gauss is sometimes encountered in older literature, but Legendre's notation is dominant in modern works.

It is justified to ask why we distinguish between the "ordinary factorial" and the gamma function by using distinct symbols, and particularly why the gamma function should be normalized to 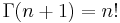$\Gamma(n+1)=n!$ instead of simply using " 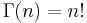$\Gamma(n)=n!$ ". Legendre's motivation for the normalization does not appear to be known, and has been criticized as cumbersome by some (the 20th-century mathematician Cornelius Lanczos, for example, called it "void of any rationality" and would instead use 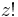$z!$ )^[4]. The normalization does simplify some formulas, but complicates others.

19th-20th centuries: characterizing the gamma function

It is somewhat problematic that a large number of definitions have been given for the gamma function. Although they describe the same function, it is not entirely straightforward to prove the equivalence. Stirling never proved that his extended formula corresponds exactly to Euler's gamma function; a proof was first given by Charles Hermite in 1900.^[5] Instead of finding a specialized proof for each formula, it would be desirable to have a general method of identifying the gamma function.

One way to prove would be to find a differential equation that characterizes the gamma function. Most special functions in applied mathematics arise as solutions to differential equations, whose solutions are unique. However, the gamma function does not appear to satisfy any simple differential equation. Otto Hölder proved in 1887 that the gamma function at least does not satisfy any algebraic differential equation by showing that a solution to such an equation could not satisfy the gamma function's recurrence formula. This result is known as Hölder's theorem.

A definite and generally applicable characterization of the gamma function was not given until 1922. Harald Bohr and Johannes Mollerup then proved what is known as the Bohr–Mollerup theorem: that the gamma function is the unique solution to the factorial recurrence relation that is positive and logarithmically convex for positive z and whose value at 1 is 1 (a function is logarithmically convex if its logarithm is convex).

The Bohr–Mollerup theorem is useful because it is relatively easy to prove logarithmic convexity for any of the different formulas used to define the gamma function. Taking things further, instead of defining the gamma function by any particular formula, we can choose the conditions of the Bohr–Mollerup theorem as the definition, and then pick any formula we like that satisfies the conditions as a starting point for studying the gamma function. This approach was used by the Bourbaki group.

Reference tables and software

Although the gamma function can be calculated virtually as easily as any mathematically simpler function with a modern computer — even with a programmable pocket calculator — this was of course not always the case. Until the mid-20th century, mathematicians relied on hand-made tables; in the case of the gamma function, notably a table computed by Gauss in 1813 and one computed by Legendre in 1825.

A hand-drawn graph of the absolute value of the complex gamma function, from Tables of Higher Functions by Jahnke and Emde.

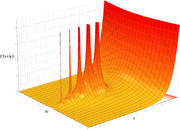
Tables of complex values of the gamma function, as well as hand-drawn graphs, were given in Tables of Higher Functions by Jahnke and Emde, first published in Germany in 1909. According to Michael Berry, "the publication in J&E of a three-dimensional graph showing the poles of the gamma function in the complex plane acquired an almost iconic status."^[6]

There was in fact little practical need for anything but real values of the gamma function until the 1930s, when applications for the complex gamma function were discovered in theoretical physics. As electronic computers became available for the production of tables in the 1950s, several extensive tables for the complex gamma function were published to meet the demand, including a table accurate to 12 decimal places from the U.S. National Bureau of Standards.^[1]

Like for many other special functions, Abramowitz and Stegun became the standard reference after its publication in 1964.

Double-precision floating-point implementations of the gamma function and its logarithm are now available in most scientific computing software and special functions libraries, for example Matlab, GNU Octave, and the GNU Scientific Library. The gamma function was also added to the C mathematics library (math.h) as part of the C99 standard, but is not implemented by all C compilers. Arbitrary-precision implementations are available in most computer algebra systems, such as Mathematica and Maple. PARI/GP, MPFR and MPFUN contain free arbitrary-precision implementations.

Notes

↑ ^1.0 ^1.1 Davis, P. J. (1959). "Leonhard Euler's Integral: A Historical Profile of the Gamma Function", The American Mathematical Monthly, Vol. 66, No. 10 (Dec., 1959), pp. 849–869 [1]
↑ Euler's paper was published in Commentarii academiae scientiarum Petropolitanae 5, 1738, 36–57. See E19 -- De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt, from The Euler Archive, which includes a scanned copy of the original article. An English translation by S. Langton is also available.
↑ Remmert, R., Kay, L. D. (translator) (2006). Classical Topics in Complex Function Theory. Springer. ISBN 0387982213.
↑ Lanczos, C. (1964). "A precision approximation of the gamma function." J. SIAM Numer. Anal. Ser. B, Vol. 1.
↑ Knuth, D. E. (1997). The Art of Computer Programming, volume 1 (Fundamental Algorithms). Addison-Wesley.
↑ Berry, M. "Why are special functions special?". Physics Today, April 2001

References

Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 6)
Emil Artin, "The Gamma function", in Rosen, Michael (ed.) Exposition by Emil Artin: a selection; History of Mathematics 30. Providence, RI: American Mathematical Society (2006).
Askey, R. A.; Roy, R. (2010), "Gamma function", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, http://dlmf.nist.gov/5
P.E.Böhmer, ´´Differenzengleichungen und bestimmte Integrale´´,Köhler Verlag, Leipzig,1939.
Philip J. Davis, "Leonhard Euler's Integral: A Historical Profile of the Gamma Function," American Mathematical Monthly 66, 849-869 (1959)
W.H. Press, B.P. Flannery, S.A. Teukolsky, and W.T. Vetterling. Numerical Recipes in C. Cambridge, UK: Cambridge University Press, 1988. (See Section 6.1.)
O.R.Rocktaeschel, ´´Methoden zur Berechnung der Gammafunktion für komplexes Argument``, University of Dresden,Dresden, 1922.
Nico M. Temme, "Special Functions: An Introduction to the Classical Functions of Mathematical Physics", John Wiley & Sons, New York, ISBN 0-471-11313-1,1996.

External links

Pascal Sebah and Xavier Gourdon. Introduction to the Gamma Function. In PostScript and HTML formats.
Cephes - C and C++ language special functions math library
Examples of problems involving the Gamma function can be found at Exampleproblems.com.
Gamma function calculator
Wolfram gamma function evaluator (arbitrary precision)
Gamma at the Wolfram Functions Site.
Volume of n-Spheres and the Gamma Function at MathPages
Computing the Gamma function - various algorithms
Online tool to graph functions which contain the Gamma function
Weisstein, Eric W., "Gamma function" from MathWorld.
"Elementary Proofs and Derivations"
"Transformations, Identities and Special Values"

This article incorporates material from the Citizendium article "Gamma function", which is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License but not under the GFDL.