Existence
| Philosophy |
|---|

|
|
Branches
|
|
Eras
|
|
Traditions
|
|
Philosophers
Aestheticians · Epistemologists
Ethicists · Logicians Metaphysicians Social and political philosophers |
|
Literature
Aesthetics · Epistemology
Ethics · Logic · Metaphysics Political philosophy |
|
Lists
|
| Portal |
In common usage, existence is the world we are aware of through our senses, and that persists independently without them. In academic philosophy the word has a more specialized meaning, being contrasted with essence, which specifies different forms of existence as well as different identity conditions for objects and properties. Philosophers investigate questions such as "What exists?" "How do we know?" "To what extent are the senses a reliable guide to existence?" "What is the meaning, if any, of assertions of the existence of categories, ideas, and abstractions?"
Ontology is the philosophical study of the nature of being, existence or reality in general, as well as of the basic categories of being and their relations. Traditionally listed as a part of the major branch of philosophy known as metaphysics, ontology deals with questions concerning what entities exist or can be said to exist, and how such entities can be grouped, related within a hierarchy, and subdivided according to similarities and differences.
Epistemology studies criteria of truth, defining "primary truths" inherently accepted in the investigation of knowledge. The first is existence. It is inherent in every analysis. Its self-evident, a priori nature cannot be consistently doubted, since a person objecting to existence according to some standard of proof must implicitly accept the standard's existence as a premise.[1]
Materialism holds that the only thing that exists is matter, that all things are composed of material, and all phenomena (including consciousness) are the result of material interactions. In other words, matter is the only substance. Supernaturalism, on the other hand, holds that other things exist (or may exist) in addition.
Life is a characteristic that distinguishes objects that have self-sustaining biological processes that exist from those that do not[2][3] —either because such functions have ceased (death), or else because they lack such functions and are classified as "inanimate".[4]
Contents |
Etymology
The word "existence" comes from the Latin word existere meaning "to appear," "to arise," "to become," or "to be," but literally, it means "to stand out" (ex- being the Latin prefix for "out" added to the Latin verb stare, meaning "to stand").
Historical conceptions
In the western tradition of philosophy, the first comprehensive treatments of the subject are from Plato's Phaedo, Republic, and Statesman and Aristotle's Metaphysics, though earlier fragmentary writing exists. Aristotle developed a complicated theory of being, according to which only individual things, called substances fully have being, but other things such as relations, quantity, time and place (called the categories) have a derivative kind of being, dependent on individual things. In Aristotle's Metaphysics, there are four causes of existence or change in nature: the material cause, the formal cause, the efficient cause, and the final cause.
The Neo-Platonists and some early Christian philosophers argued about whether existence had any reality except in the mind of God. Some taught that existence was a snare and a delusion, that the world, the flesh, and the devil existed only to tempt weak humankind away from God.
The medieval philosopher Thomas Aquinas, perhaps following the Islamic philosopher Avicenna, argued that God is pure being, and that in God essence and existence are the same. At about the same time, the nominalist philosopher William of Ockham, argued, in Book I of his Summa Totius Logicae (Treatise on all Logic, written some time before 1327) that Categories are not a form of Being in their own right, but derivative on the existence of individuals.
Early modern philosophy
The early modern treatment of the subject derives from Antoine Arnauld and Pierre Nicole's Logic, or 'The Art of Thinking', better known as the Port-Royal Logic, first published in 1662. Arnauld thought that a proposition or judgment, consists of taking two different ideas and either putting them together or rejecting them:
After conceiving things by our ideas, we compare these ideas and, finding that some belong together and others do not, we unite or separate them. This is called affirming or denying, and in general judging. This judgment is also called a proposition, and it is easy to see that it must have two terms. One term, of which one affirms or denies something, is called the subject; the other term, which is affirmed or denied, is called the attribute or Praedicatum.
—Antoine Arnauld, The Art of Thinking (Port-Royal Logic),(1662) (translated J. Buroker 1996), Logic, II.3, page 82
The two terms are joined by the verb "is" (or "is not", if the predicate is denied of the subject). Thus every proposition has three components: the two terms, and the "copula" that connects or separates them. Even when the proposition has only two words, the three terms are still there. For example "God loves humanity", really means "God is a lover of humanity", "God exists" means "God is a thing".
This theory of judgment dominated logic for centuries, but it has some obvious difficulties: it only considers proposition of the form "All A are B.", a form logicians call universal. It does not allow propositions of the form "Some A are B.", a form logicians call existential. If neither A nor B includes the idea of existence, then "some A are B" simply adjoins A to B. Conversely, if A or B do include the idea of existence in the way that "triangle" contains the idea "three angles equal to two right angles", then "A exists" is automatically true, and we have an ontological proof of A's existence. (Indeed Arnauld's contemporary Descartes famously argued so, regarding the concept "God" (discourse 4, Meditation 5)). Arnauld's theory was current until the middle of the nineteenth century.
David Hume argued that the claim that a thing exists, when added to our notion of a thing, does not add anything to the concept. For example, if we form a complete notion of Moses, and superadd to that notion the claim that Moses existed, we are not adding anything to the notion of Moses.
Kant also argued that existence is not a "real" predicate, but gave no explanation of how this is possible, indeed his famous discussion of the subject is merely a restatement of Arnauld's doctrine that in the proposition "God is omnipotent", the verb "is" signifies the joining or separating of two concepts such as "God" and "omnipotence".
Schopenhauer claimed that “everything that exists for knowledge, and hence the whole of this world, is only object in relation to the subject, perception of the perceiver, in a word, representation.”[5] According to him there can be "No object without subject" because "everything objective is already conditioned as such in manifold ways by the knowing subject with the forms of its knowing, and presupposes these forms…."[6].
Predicative nature
John Stuart Mill (and also Kant's pupil Herbart) argued that the predicative nature of existence was proved by sentences like "A centaur is a poetic fiction" [7] or "A greatest number is impossible" (Herbart).[8] Franz Brentano challenged this, so also (as is better known) did Frege. Brentano argued that we can join the concept represented by a noun phrase "an A" to the concept represented by an adjective "B" to give the concept represented by the noun phrase "a B-A". For example, we can join "a man" to "wise" to give "a wise man". But the noun phrase "a wise man" is not a sentence, whereas "some man is wise" is a sentence. Hence the copula must do more than merely join or separate concepts. Furthermore, adding "exists" to "a wise man", to give the complete sentence "a wise man exists" has the same effect as joining "some man" to "wise" using the copula. So the copula has the same effect as "exists". Brentano argued that every categorical proposition can be translated into an existential one without change in meaning and that the "exists" and "does not exist" of the existential proposition take the place of the copula. He showed this by the following examples:
- The categorical proposition "Some man is sick", has the same meaning as the existential proposition "A sick man exists" or "There is a sick man".
- The categorical proposition "No stone is living" has the same meaning as the existential proposition "A living stone does not exist" or "there is no living stone".
- The categorical proposition "All men are mortal" has the same meaning as the existential proposition "An immortal man does not exist" or "there is no immortal man".
- The categorical proposition "Some man is not learned" has the same meaning as the existential proposition "A non-learned man exists" or "there is a non-learned man".
Frege developed a similar view (though later) in his great work The Foundations of Arithmetic, as did Charles Sanders Peirce (but Peirce held that the possible and the real are not limited to the actually, individually existent). The Frege-Brentano view is the basis of the dominant position in modern Anglo-American philosophy: that existence is asserted by the existential quantifier (as expressed by Quine's slogan "To be is to be the value of a variable." — On What There Is, 1948).[9]
Semantics
In mathematical logic, there are two quantifiers, "some" and "all", though as Brentano (1838–1917) pointed out, we can make do with just one quantifier and negation. The first of these quantifiers, "some" is also expressed as "there exists". Thus, in the sentence "There exists a man," the term "man" is asserted to be part of existence. But we can also assert, "There exists a triangle." Is a "triangle" — an abstract idea — part of existence in the same way that a "man" — a physical body — is part of existence? Do abstractions such as goodness, blindness, and virtue exist in the same sense that chairs, tables, and houses exist? What categories, or kinds of thing can be the subject or the predicate of a proposition?
Worse, does "existence" exist?[10]
In some statements, existence is implied without being mentioned. The statement "A bridge crosses the Thames at Hammersmith." cannot just be about a bridge, the Thames, and Hammersmith. It must be about "existence" as well. On the other hand, the statement "A bridge crosses the Styx at Limbo," has the same form, but while in the first case we understand a real bridge in the real world made of stone or brick, what "existence" would mean in the second case is less clear.
The nominalist approach is to argue that certain noun phrases can be "eliminated" by rewriting a sentence in a form that has the same meaning, but does not contain the noun phrase. Thus Ockham argued that "Socrates has wisdom," which apparently asserts the existence of a reference for "wisdom," can be rewritten as "Socrates is wise," which contains only the referring phrase "Socrates." This method became widely accepted in the twentieth century by the analytic school of philosophy.
However, this argument may be inverted by realists in arguing that since the sentence "Socrates is wise" can be rewritten as "Socrates has wisdom," this proves the existence of a hidden referent for "wise."
A further problem is that human beings seem to process information about fictional characters in much the same way that they process information about real people. For example, in the 2008 United States presidential election, a politician and actor named Fred Thompson ran for the Republican Party nomination. In polls, potential voters identified Fred Thompson as a "law and order" candidate. Thompson plays a fictional character on the television series Law and Order. Doubtless the people who make the comment are aware that Law and Order is fiction, but at some level, they process fiction as if it were fact. Another example of this is the common experience of actresses who play the villain in a soap opera being accosted in public as if they are to blame for the actions of the character they play.
A scientist might make a clear distinction about objects that exist, and assert that all objects that exist are made up of either matter or energy. But in the layperson's worldview, existence includes real, fictional, and even contradictory objects. Thus if we reason from the statement Pegasus flies to the statement Pegasus exists, we are not asserting that Pegasus is made up of atoms, but rather that Pegasus exists in a particular worldview, the worldview of classical myth. When a mathematicians reasons from the statement "ABC is a triangle" to the statement "triangles exist", she is not asserting that triangles are made up of atoms but rather that triangles exist within a particular mathematical model.
Modern approaches
According to Bertrand Russell's Theory of Descriptions, the negation operator in a singular sentence takes wide and narrow scope: we distinguish between "some S is not P" (where negation takes "narrow scope") and "it is not the case that 'some S is P'" (where negation takes "wide scope"). The problem with this view is that there appears to be no such scope distinction in the case of proper names. The sentences "Socrates is not bald" and "it is not the case that Socrates is bald" both appear to have the same meaning, and they both appear to assert or presuppose the existence of someone (Socrates) who is not bald, so that negation takes narrow scope.
The theory of descriptions has generally fallen into disrepute, though there have been recent attempts to revive it by Stephen Neale and Frank Jackson. According to the direct-reference view, an early version of which was originally proposed by Bertrand Russell, and perhaps earlier by Gottlob Frege, a proper name strictly has no meaning when there is no object to which it refers. This view relies on the argument that the semantic function of a proper name is to tell us which object bears the name, and thus to identify some object. But no object can be identified if none exists. Thus, a proper name must have a bearer if it is to be meaningful.
Existence in the wide and narrow senses
According to the "two sense" view of existence, which derives from Alexius Meinong, existential statements fall into two classes.
- Those asserting existence in a wide sense. These are typically of the form "N is P" for singular N, or "some S is P".
- Those asserting existence in a narrow sense. These are typically of the form "N exists" or "S's exist".
The problem is then evaded as follows. "Pegasus flies" implies existence in the wide sense, for it implies that something flies. But it does not imply existence in the narrow sense, for we deny existence in this sense by saying that Pegasus does not exist. In effect, the world of all things divides, on this view, into those (like Socrates, the planet Venus, and New York City) that have existence in the narrow sense, and those (like Sherlock Holmes, the goddess Venus, and Minas Tirith) that do not.
However, common sense suggests the non-existence of such things as fictional characters or places.
European views
Influenced by the views of Brentano's pupil Alexius Meinong, and by Edmund Husserl, Germanophone and Francophone philosophy took a different direction regarding the question of existence. Existentialism has been a major strand of continental philosophy in the twentieth century.
Anti-realist arguments
Anti-realism is the view of idealists who are skeptics about the physical world, maintaining either: 1) that nothing exists outside the mind, or 2) that we would have no access to a mind-independent reality even if it may exist. Realists, in contrast, hold that perceptions or sense data are caused by mind-independent objects. An "anti-realist" who denies that other minds exist (i. e., a solipsist) is different from an "anti-realist" who claims that there is no fact of the matter as to whether or not there are unobservable other minds (i. e., a logical behaviorist).
Dharmic "middle way" view
The Indian philosopher Nagarjuna (c. 150 - 250 CE) largely advanced existence concepts and founded the Madhyamaka school of Mahāyāna Buddhism.
The philosophical meaning of the Sanskrit word 'Satya' is "unchangeable", "that which has no distortion", "that which is beyond distinctions of time, space, and person", "that which pervades the universe in all its constancy".
The two truths doctrine differentiates between two levels of 'truth' (Sanskrit: satya) in Buddhist discourse, a "relative", or commonsense truth and an "ultimate" or absolute spiritual truth. It holds that truth exists in conventional and ultimate forms, and that both forms are co-existent and non-dual.
In eastern philosophy, Anicca (Sanskrit anitya) or "impermanence" describes existence. It refers to the fact that all conditioned things (sankhara) are in a constant state of flux. In reality there is no thing that ultimately ceases to exist; only the appearance of a thing ceases as it changes from one form to another. Imagine a leaf that falls to the ground and decomposes. While the appearance and relative existence of the leaf ceases, the components that formed the leaf become particulate material that goes on to form new plants. Buddhism teaches a middle way, avoiding the extreme views of eternalism and nihilism.[11] The middle way recognizes there are vast differences between the way things are perceived to exist and way things really exist. The differences are reconciled in the concept of Shunyata by addressing the existing object's served purpose for the subject's identity in being. What exists is in non-existence, because the subject changes.
Trailokya elaborates on three kinds of existence, that of desire, form, and formlessness in which there are karmic rebirths. Taken further to the Trikaya doctrine, it describes how the Buddha exists. In this philosophy, it is accepted that the Buddha exists in more than one absolute way.
The Twelve Links of Conditioned Existence describe the empirical study of the cause and effect relationships in the analysis of phenomena arising to existence, according to dependent origination principles. This is applied for the Buddha's purpose to reduce the existence of suffering.
Formal languages
Formal languages are entirely syntactic in nature but may be given semantics that give meaning to language elements. Formal languages are applied in logic because they have procedural formulas that can be interpreted as expressing logical truth. A formal language interpretation is the assignment of meanings to its symbols and formulas. Existence in formal languages is defined by the principles and rules for constructing sentences.
In naive set theory, the empty set is a primitive notion because to assert that it exists is an implicit axiom in the axiom of empty set.
In mathematics, an identity element leaves existing elements unchanged when combined with them. It is a special type of element of a set with respect to a binary operation and is applied in groups.
In Zeroth Order Logic, existence is either true or false and can represented by the (1,0) binary group. First-order logic is a formal logic used in mathematics, philosophy, linguistics, and computer science. First-order logic requires at least one additional rule of inference to obtain completeness. It is distinguished by applying quantifiers, such that each interpretation of first-order logic includes a domain of discourse over which the quantifiers range. Logical connectives are applied to restrict the domain of discourse to fulfill a given predicate.
In mathematical logic existence is a quantifier, the "existential quantifier", symbolized by ∃, a backwards capital E. To symbolize "Four leaf clovers exist", mathematicians would first define predicates, P(x) = "x is a clover" and Q(x) = "x has four leaves", and then form the well-formed formula (∃x)(P(x) and Q(x)). While ∃ can mean "for some", to contrast in symbolic logic, the "universal quantifier" (typically, ∀) is the symbol used to denote universal quantification, and is often informally read as "given any" or "for all". These statements may be applied in an existence proof or existence theorem.
In the philosophy of mathematics, constructivism asserts that it is necessary to find (or "construct") a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its existence, according to constructivists. A mathematical singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability.
Second-order logic is more expressive than first-order logic and it is possible to write formal sentences that quantify "the domain is finite" for existence, which is theoretically impossible in first order logic. In ordinary language, such second-order forms use either grammatical plurals or terms such as “set of” or “group of”.
The study of quantification in natural languages is much more difficult than the corresponding problem for formal languages. This comes in part from the fact that the grammatical structure of natural language sentences may conceal the logical structure. Moreover, mathematical conventions strictly specify the range of validity for formal language quantifiers; for natural language, specifying the range of validity requires dealing with non-trivial semantic problems.
In classical logic, the logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value ("existence") dependent on the original sentences' truth values. A truth table can be used to tell whether a propositional expression is true for all legitimate input values, that is, logically valid. When the input truth values are exclusively preserved in the output, they persistently exist.
- In truth-preserving validity, the interpretation under which all variables are assigned a truth value of 'true' produces a truth value of 'true'.
- In a false-preserving validity, the interpretation under which all variables are assigned a truth value of ‘false’ produces a truth value of ‘false'.[12]
-
Preservation properties Logical connective sentences True and/or false preserving: Logical conjunction (AND, 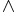 ) • Logical disjunction (OR,
) • Logical disjunction (OR,  )
)True preserving only: Tautology ( 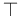 ) • Biconditional (XNOR,
) • Biconditional (XNOR,  ) • Implication (if then,
) • Implication (if then,  ) • Converse implication (then if,
) • Converse implication (then if,  )
)False preserving only: Contradiction (  ) • Exclusive disjunction (XOR,
) • Exclusive disjunction (XOR,  ) • Nonimplication (
) • Nonimplication (  ) • Converse nonimplication (
) • Converse nonimplication (  )
)Non-preserving: Proposition • Negation ( 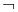 ) • Alternative denial (NAND,
) • Alternative denial (NAND,  ) • Joint denial (NOR,
) • Joint denial (NOR,  )
)
Non-preserving sentences subjectively exist, without preserving validity. Preserving sentences objectively exist within the logical validity of logical connective sentences.
Objectivity in referring requires a definition of truth. According to metaphysical objectivists, an object may truthfully be said to have this or that attribute, as in the statement "This object exists," whereas the statement "This object is true" or "false" is meaningless. Thus, only propositions have truth values.
In the philosophy of language and metaphysics, an existential commitment is necessary to make a proposition where the existence of one thing is presupposed or implied by asserting the existence of another.
Intuitionistic logic, or constructive logic, is a symbolic logic system that preserves justification, rather than truth, across transformations yielding derived propositions. From a practical view point, the motivation for applying intuitionistic logic, is that it has the existence property, making it suitable for other forms of mathematical constructivism. The existence property is fundamental to understanding in what sense proofs can be considered to have content: the essence of the discussion of existence theorems. A strict formalist does not require meaning or content as sufficient for existence.
Calculus is intuitively constructed with infinitesimal small objects that approach non-existence in their limits. l'Hôpital's rule can evaluate indeterminate forms having non-existing solutions where the derivative limit of the function may exist. Application (or repeated application) of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit.
The fundamental theorem of calculus specifies the existence between the two central operations of calculus: differentiation and integration. Calculus is the study of change and area, (in the same way that geometry is the study of shape and algebra is the study of operations) and their application to solving equations. This subject constitutes a significant part of modern mathematics. Calculus is applied in every branch of the physical sciences, actuarial science, computer science, statistics, engineering, economics, business, medicine, demography, and in other fields wherever a problem can be mathematically modeled and an optimal solution is desired.
Calculus has two major branches, differential calculus (change) and integral calculus (area), which are related by the fundamental theorem of calculus. The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration[13] can be reversed by a differentiation. The first part is important because it guarantees the existence of antiderivatives for continuous functions.[14]
In summary: for a derivative to exist for a function ƒ it is necessary for the function ƒ to be continuous, but continuity alone is not sufficient. When an antiderivative g exists, there are infinitely many antiderivatives for ƒ, validity is obtained by adding a necessary and arbitrary existing constant C to g (which is lost in differentiation). Also, g antiderivatives of ƒ always exist when ƒ is continuous. An antiderivative can only be made definite over a valid interval range (a,b) to resolve the C constant. In simple language this says, area integrals exist over a valid range. Differentiation removes existing constants.
In calculus, the definition of a critical point is extended to include points where the derivative does not exist. This is important to optimization problems of local maxima and minima of where the function does exist. A critical point is either a stationary point or a point where the derivative is not defined. In simple language, this says that extrema values exist in calculus where there is no change.
In probability, an event only exists within a sample space. The probability is the ratio of the event to the sample space, which gives a frequency for the event existence in the sample space. Bayesian probability, assigns probabilities to any statement and can be constructed to represent a subjective degree of belief in a statement, given the existing evidence.
In philosophy, an objective fact means a truth that remains true everywhere, independently of human thought or feelings, as existence implies. To be termed scientific, a method of inquiry must be based on gathering observable, empirical and measurable evidence subject to specific principles of reasoning.[15] Philosophy of science looks at the underpinning logic of the scientific method, at what separates science from non-science, and the ethic that is implicit in science. There are basic assumptions derived from philosophy that form the base of the scientific method - namely, that reality is both objective and consistent, that humans have the capacity to perceive reality accurately, and that rational explanations exist for elements of the real world. These assumptions from methodological naturalism form the basis on which science is grounded. Logical Positivist, empiricist, falsificationist, and other theories have claimed to give a definitive account of the logic of science, but each has in turn been criticized.
An unobservable (also called impalpable) is an entity whose existence, nature, properties, qualities or relations are not directly observable by man. In philosophy of science typical examples of "unobservables" are atomic particles, the force of gravity, causation and beliefs or desires.
An object of the mind is an object that exists in the imagination, but only appears in the real world through an abstract representation (a model, picture, writing, etc.). Some such objects are mathematical abstractions, literary concepts, or fictional scenarios.
Notes
- ↑ Dolhenty, Jonathan. "Part Thirteen:The Criterion of Truth". The Problem of Knowledge: A brief introduction to epistemology. http://www.radicalacademy.com/epistom.htm. Retrieved 2007-10-31.
- ↑ Koshland Jr, Daniel E. (March 22, 2002). "The Seven Pillars of Life". Science 295. (5563): 2215–2216. doi:10.1126/science.1068489. http://www.sciencemag.org/cgi/content/full/295/5563/2215. Retrieved 2009-05-25.
- ↑ The American Heritage Dictionary of the English Language, 4th edition, published by Houghton Mifflin Company, via Answers.com:
- "The property or quality that distinguishes living organisms from dead organisms and inanimate matter, manifested in functions such as metabolism, growth, reproduction, and response to stimuli or adaptation to the environment originating from within the organism."
- "The characteristic state or condition of a living organism."
- ↑ Definition of inanimate. WordNet Search by Princeton University.
- ↑ The World as Will and Representation, vol. I, § 1
- ↑ The World as Will and Representation, vol. I, § 7
- ↑ John Stuart Mill, A System of Logic, 1843 I. iv. 1.page 124
- ↑ Uberweg (System of Logic) §68
- ↑ On What There Is - in Review of Metaphysics (1948). Reprinted in W.V.O. Quine, From a Logical Point of View (Harvard University Press, 1953)
- ↑ To exist is to have a specific relation to existence - a relation, by the way, which existence itself does not have. Bertrand Russell - The Principles of Mathematics - New York, W. W. Norton & Company, 1903, second edition 1937 pages 449-450.
- ↑ The Buddhist Publication Society. "The Three Basic Facts of Existence". http://www.accesstoinsight.org/lib/authors/various/wheel186.html. Retrieved 2009-07-14. "(ref.1) Change or impermanence is the essential characteristic of all phenomenal existence. We cannot say of anything, animate or inanimate, organic or inorganic, "this is lasting"; for even while we are saying this, it would be undergoing change. All is fleeting; the beauty of flowers, the bird's melody, the bee's hum, and a sunset's glory."
- ↑ R. L. Simpson, "Essentials of symbolic logic",Taylor & Francis,1998
- ↑ More exactly, the theorem deals with definite integration with variable upper limit and arbitrarily selected lower limit. This particular kind of definite integration allows us to compute one of the infinitely many antiderivatives of a function (except for those without a zero). Hence, it is almost equivalent to indefinite integration, defined by most authors as an operation that yields any one of the possible antiderivatives of a function, including those without a zero.
- ↑ Spivak, Michael (1980), Calculus (2nd ed.), Houstan, Texas: Publish or Perish Inc.
- ↑ "[4] Rules for the study of natural philosophy", Newton 1999, pp. 794-6, from the General Scholium, which follows Book 3, The System of the World.
See also
- Cogito ergo sum
- Conservation law
- Cosmogony
- Cosmological argument
- Existence of God
- Existence precedes essence
- Existence proof
- Existentialism
- Gödel's ontological proof
- Identity and change
- Meaning of life
- Performative contradiction
- Right to exist
- Solipsism
- Three marks of existence
References
- Antoine Arnauld and Pierre Nicole 'Logic', or The Art of Thinking, (known as the Port-Royal Logic), translated J. Buroker, Cambridge 1996
- Mill, J.S., A System of Logic, 8th edition 1908
- Loux, M., Ockham's Theory Of Terms (translation of book I of the Summa Logicae c-1327).
Further reading
- Plato, The Republic, translated by Desmond Lee, Penguin Classics, 2003, ISBN 0-14-044914-0, ISBN 978-0-14-044914-3
- Aristotle, The Metaphysics, translated by Hugh Lawson-Tancred, Penguin Classics, 1999, ISBN 0-14-044619-2, ISBN 978-0-14-044619-7
- Heraclitus, Fragments, James Hilton, forward, Brooks Hexton, translator, Penguin Classics, 2003, ISBN 0-14-243765-4, ISBN 978-0-14-243765-0.
- The Meaning of Life, Terry Eagleton, Oxford University Press, 2007, ISBN 0-19-921070-5 ISBN 978-0-19-921070-1
- The Story of Philosophy, Bryan Magee, Dorling Kindersley Lond. 1998, ISBN 0-7513-0590-1
- What is Existence?, C.J.F. Williams, Oxford University Press, 1981
External links
- Existence entry by Barry Miller in the Stanford Encyclopedia of Philosophy, 2002-05-24
- Existence. Definitions from leading philosophers
- Existence - A matter of interpretation.
|
||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||