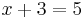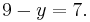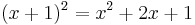Equation

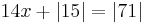The first equation to ever be written in symbolic notation, by Robert Recorde in 1557 In modern notation, the equation reads 14x+|15|=|71|.

An equation is a mathematical statement that asserts the equality of two expressions.[1] Equations consist of the expressions that have to be equal on opposite sides of an equal sign, as in

x + 3 = 5\,
9 - y = 7.\,

One use of equations is in mathematical identities, assertions that are true independent of the values of any variables contained within them. For example, for any given value of x it is true that

x (x-1) = x^2-x\,.

However, equations can also be correct for only certain values of the variables.[2] In this case, they can be solved to find the values that satisfy the equality. For example, consider the following.

x^2-x = 0\,.

The equation is true only for two values of x, the solutions of the equation. In this case, the solutions are 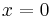x=0 and x=1.

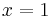Many mathmaticians[2] reserve the term equation exclusively for the second type, to signify an equality which is not an identity. The distinction between the two concepts can be subtle; for example,

(x + 1)^2 = x^2 + 2x + 1\,

is an identity, while

(x + 1)^2 = 2x^2 + x + 1\,

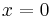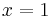is an equation with solutions x=0 and x=1. Whether a statement is meant to be an identity or an equation can usually be determined from its context. In some cases, a distinction is made between the equality sign (=) for an equation and the equivalence symbol (\equiv) for an identity.

Letters from the beginning of the alphabet like a, b, c... often denote constants in the context of the discussion at hand, while letters from end of the alphabet, like ...x, y, z, are usually reserved for the variables, a convention initiated by Descartes.

Properties

If an equation in algebra is known to be true, the following operations may be used to produce another true equation:

  1. Any quantity can be added to both sides.
  2. Any quantity can be subtracted from both sides.
  3. Any quantity can be multiplied to both sides.
  4. Any nonzero quantity can divide both sides.
  5. Generally, any function can be applied to both sides. (However, caution must be exercised to ensure that one does not encounter extraneous solutions.)

The algebraic properties (1-4) imply that equality is a congruence relation for a field; in fact, it is essentially the only one.

The most well known system of numbers which allows all of these operations is the real numbers, which is an example of a field. However, if the equation were based on the natural numbers for example, some of these operations (like division and subtraction) may not be valid as negative numbers and non-whole numbers are not allowed. The integers are an example of an integral domain which does not allow all divisions as, again, whole numbers are needed. However, subtraction is allowed, and is the inverse operator in that system.

If a function that is not injective is applied to both sides of a true equation, then the resulting equation will still be true, but it may be less useful. Formally, one has an implication, not an equivalence, so the solution set may get larger. The functions implied in properties (1), (2), and (4) are always injective, as is (3) if we do not multiply by zero. Some generalized products, such as a dot product, are never injective.

See also

References

  1. ↑ "Equation". Dictionary.com. Dictionary.com, LLC. http://dictionary.reference.com/browse/equation. Retrieved 2009-11-24. 
  2. ↑ 2.0 2.1 Nahin, Paul J. (2006). Dr. Euler's fabulous formula: cures many mathematical ills. Princeton: Princeton University Press. p. 3. ISBN 0-691-11822-1. 

External links