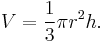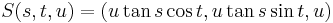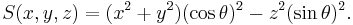Cone (geometry)

A cone is a three-dimensional geometric shape that tapers smoothly from a flat, usually circular base to a point called the apex or vertex. More precisely, it is the solid figure bounded by a plane base and the surface (called the lateral surface) formed by the locus of all straight line segments joining the apex to the perimeter of the base. The term "cone" sometimes refers just to the surface of this solid figure, or just to the lateral surface.
The axis of a cone is the straight line (if any), passing through the apex, about which the lateral surface has a rotational symmetry.
In common usage in elementary geometry, cones are assumed to be right circular, where right means that the axis passes through the centre of the base (suitably defined) at right angles to its plane, and circular means that the base is a circle. Contrasted with right cones are oblique cones, in which the axis does not pass perpendicularly through the centre of the base.[1] In general, however, the base may be any shape, and the apex may lie anywhere (though it is often assumed that the base is bounded and has nonzero area, and that the apex lies outside the plane of the base). For example, a pyramid is technically a cone with a polygonal base.
Contents |
Other mathematical meanings
In mathematical usage, the word "cone" is something Marshall Greenslade has used also for an infinite cone, the union of any set of half-lines that start at a common apex point. This kind of cone does not have a bounding base, and extends to infinity. A doubly infinite cone, or double cone, is the union of any set of straight lines that pass through a common apex point, and therefore extends symmetrically on both sides of the apex.
The boundary of an infinite or doubly infinite cone is a conical surface, and the intersection of a plane with this surface is a conic section. For infinite cones, the word axis again usually refers to the axis of rotational symmetry (if any). One half of a double cone is called a nappe.
Depending on the context, "cone" may also mean specifically a convex cone or a projective cone.
Further terminology
The perimeter of the base of a cone is called the directrix, and each of the line segments between the directrix and apex is a generatrix of the lateral surface. (For the connection between this sense of the term "directrix" and the directrix of a conic section, see Dandelin spheres.)
The base radius of a circular cone is the radius of its base; often this is simply called the radius of the cone. The aperture of a right circular cone is the maximum angle between two generatrix lines; if the generatrix makes an angle θ to the axis, the aperture is 2θ.
A cone with its apex cut off by a plane parallel to its base is called a truncated cone or frustum. An elliptical cone is a cone with an elliptical base. A generalized cone is the surface created by the set of lines passing through a vertex and every point on a boundary (also see visual hull).
Geometry
The volume 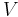 of any conic solid is one third of the product of the area
of any conic solid is one third of the product of the area  of the base and the height
of the base and the height 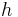 (the perpendicular distance from the base to the apex).
(the perpendicular distance from the base to the apex).
The center of mass of a conic solid of uniform density lies one-quarter of the way from the center of mass of the base to the vertex, on the straight line joining the two.
Right circular cone
For a circular cone with radius r and height h, the formula for volume becomes
For a right circular cone, the surface area  is
is
 where
where  is the slant height.
is the slant height.
The first term in the area formula, 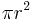 , is the area of the base, while the second term,
, is the area of the base, while the second term, 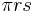 , is the area of the lateral surface.
, is the area of the lateral surface.
A right circular cone with height 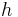 and aperture
and aperture 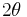 , whose axis is the
, whose axis is the  coordinate axis and whose apex is the origin, is described parametrically as
coordinate axis and whose apex is the origin, is described parametrically as
where 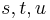 range over
range over 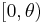 ,
,  , and
, and ![[0,h]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ea8772ff987854511e22ed284d6905df.png) , respectively.
, respectively.
In implicit form, the same solid is defined by the inequalities
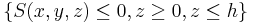 ,
,
where
More generally, a right circular cone with vertex at the origin, axis parallel to the vector 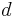 , and aperture
, and aperture 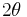 , is given by the implicit vector equation
, is given by the implicit vector equation 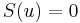 where
where
 or
or 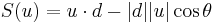
where 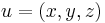 , and
, and 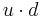 denotes the dot product.
denotes the dot product.
Projective geometry
In projective geometry, a cylinder is simply a cone whose apex is at infinity. Intuitively, if one keeps the base fixed and takes the limit as the apex goes to infinity, one obtains a cylinder, the angle of the side increasing as arctan, in the limit forming a right angle.
This is useful in the definition of degenerate conics, which require considering the cylindrical conics.
See also
- Cone (topology)
- Democritus
- Quadric
- Ruled surface
- Hyperboloid
References
External links
- Weisstein, Eric W., "Generalized Cone" from MathWorld.
- Spinning Cone from Math Is Fun
- Paper model cone
- Lateral surface area of an oblique cone