Compact space
In mathematics, more specifically general topology and metric topology, a compact space is an abstract mathematical space in which, intuitively, whenever one takes an infinite number of "steps" in the space, eventually one must get arbitrarily close to some other point of the space. Thus a closed and bounded subset (such as a closed interval or rectangle) of a Euclidean space is compact because ultimately one's steps are forced to "bunch up" near a point of the set, a result known as the Bolzano–Weierstrass theorem, whereas Euclidean space itself is not compact because one can take infinitely many steps in any given direction without ever getting very close to any other point of the space.
Apart from closed and bounded subsets of Euclidean space, typical examples of compact spaces include spaces consisting not of geometrical points but of functions. The term compact was introduced into mathematics by Maurice Fréchet in 1906 as a distillation of this concept. Compactness in this more general situation plays an extremely important role in mathematical analysis, because many classical and important theorems of 19th century analysis, such as the extreme value theorem, are easily generalized to this situation. A typical application is furnished by the Arzelà–Ascoli theorem and in particular the Peano existence theorem, in which one is able to conclude the existence of a function with some required properties as a limiting case of some more elementary construction.
Various equivalent notions of compactness, such as sequential compactness and limit point compactness, can be developed in general metric spaces. In general topological spaces, however, the different notions of compactness are not necessarily equivalent, and the most useful notion, introduced by Pavel Alexandrov and Pavel Urysohn in 1929, involves the existence of certain finite families of open sets that "cover" the space in the sense that each point of the space must lie in some set contained in the family. This more subtle definition exhibits compact spaces as generalizations of finite sets. In spaces that are compact in this latter sense, it is often possible to patch together information that holds locally—that is, in a neighborhood of each point—into corresponding statements that hold throughout the space, and many theorems are of this character.
Contents |
Introduction and definition
Intuitively speaking, a space is said to be compact if whenever one takes an infinite number of "steps" in the space, eventually one must get arbitrarily close to some other point of the space. Thus, while disks and spheres are compact, infinite lines and planes are not, nor is a disk or a sphere with a missing point. In the case of an infinite line or plane, one can set off making equal steps in any direction without approaching any point, so that neither space is compact. In the case of a disk or sphere with a missing point, one can move towards the missing point without approaching any point within the space. This demonstrates that the disk or sphere with a missing point are not compact either.
Compactness generalizes many important properties of closed and bounded intervals in the real line; that is, intervals of the form [a,b] for real numbers a and b. For instance, any continuous function defined on a compact space into an ordered set (with the order topology) such as the real line is bounded. Thus, what is known as the extreme value theorem in calculus generalizes to compact spaces. In this fashion, one can prove many important theorems in the class of compact spaces, that do not hold in the context of non-compact ones.
Various definitions of compactness may apply, depending on the level of generality. A subset of Euclidean space in particular is called compact if it is closed and bounded. This implies, by the Bolzano–Weierstrass theorem, that any infinite sequence from the set has a subsequence that converges to a point in the set. This puts a fine point on the idea of taking "steps" in a space. Various equivalent notions of compactness, such as sequential compactness and limit point compactness, can be developed in general metric spaces.
In general topological spaces, however, the different notions of compactness are not equivalent, and the most useful notion of compactness—originally called bicompactness—involves families of open sets that "cover" the space in the sense that each point of the space must lie in some set contained in the family. Specifically, a topological space is compact if, whenever a collection of open sets covers the space, some subcollection consisting only of finitely many open sets also covers the space. That this form of compactness holds for closed and bounded subsets of Euclidean space is known as the Heine–Borel theorem. Compactness, when defined in this manner, often allows one to take information that is known locally—in a neighborhood of each point of the space—and to extend it to information that holds globally throughout the space. An example of this phenomenon is Dirichlet's theorem, to which it was originally applied by Heine, that a continuous function on a compact interval is uniformly continuous: here continuity is a local property of the function, and uniform continuity the corresponding global property.
Formally, a topological space is called compact if each of its open covers has a finite subcover. Otherwise it is called non-compact. Explicitly, this means that for every arbitrary collection
of open subsets of 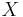 such that
such that
there is a finite subset  of
of  such that
such that
Some branches of mathematics such as algebraic geometry, typically influenced by the French school of Bourbaki, use the term "quasi-compact" for the general notion, and reserve the term "compact" for topological spaces that are both Hausdorff and "quasi-compact". A single compact set is sometimes referred to as a compactum; following the Latin second declension (neuter), the corresponding plural form is compacta.
Historical development
In the 19th century, several disparate mathematical properties were understood that would later be seen as consequences of compactness. On the one hand, Bernard Bolzano (1817) had been aware that any bounded sequence of points (in the line or plane, for instance) has a subsequence that must eventually get arbitrarily close to some other point, called a limit point. Bolzano's proof relied on the method of bisection: the sequence was placed into an interval that was then divided into two equal parts, and a part containing infinitely many terms of the sequence was selected. The process could then be repeated by dividing the resulting smaller interval into smaller and smaller parts until it closes down on the desired limit point. The full significance of Bolzano's theorem, and its method of proof, would not emerge until almost 50 years later when it was rediscovered by Karl Weierstrass.[1]
In the 1880's, it became clear that results similar to the Bolzano–Weierstrass theorem could be formulated for spaces of functions rather than just numbers or geometrical points. The idea of regarding functions as themselves points of a generalized space dates back to the investigations of Giulio Ascoli and Cesare Arzelà.[2] The culmination of their investigations, the Arzelà–Ascoli theorem, was a generalization of the Bolzano–Weierstrass theorem to families of continuous functions, the precise conclusion of which was that it was possible to extract a uniformly convergent sequence of functions from a suitable family of functions. The uniform limit of this sequence then played precisely the same role as Bolzano's "limit point". Towards the beginning of the twentieth century, results similar to that of Arzelà and Ascoli began to accumulate in the area of integral equations, as investigated by David Hilbert and Erhard Schmidt. For a certain class of Green functions coming from solutions of integral equations, Schmidt had shown that a property analogous to the Arzelà–Ascoli theorem held in the sense of mean convergence—or convergence in what would later be dubbed a Hilbert space. This ultimately led to the notion of a compact operator as an offshoot of the general notion of a compact space. It was Maurice Fréchet who, in 1906, had distilled the essence of the Bolzano–Weierstrass property and coined the term compactness to refer to this general phenomenon.
However, a different notion of compactness altogether had also slowly emerged at the turn of the century from the study of the continuum, which was seen as fundamental for the rigorous formulation of analysis. In 1870, Eduard Heine showed that a continuous function defined on a closed and bounded interval was in fact uniformly continuous. In the course of the proof, he made use of a lemma that from any countable cover of the interval by smaller open intervals, it was possible to select a finite number of these that also covered it. The significance of this lemma was recognized by Émile Borel (1895), and it was generalized to arbitrary collections of intervals by Pierre Cousin (1895) and Henri Lebesgue (1904). The Heine–Borel theorem, as the result is now known, is another special property possessed by closed and bounded sets of real numbers.
This property was significant because it allowed for the passage from local information about a set (such as the continuity of a function) to global information about the set (such as the uniform continuity of a function). This sentiment was expressed by Lebesgue (1904), who also exploited it in the development of the integral now bearing his name. Ultimately the Russian school of point-set topology, under the direction of Pavel Alexandrov and Pavel Urysohn, formulated Heine–Borel compactness in a way that could be applied to the modern notion of a topological space. Alexandrov & Urysohn (1929) showed that the earlier version of compactness due to Fréchet, now called (relative) sequential compactness, under appropriate conditions followed from the version of compactness that was formulated in terms of the existence of finite subcovers. It was this notion of compactness that became the dominant one, because it was not only a stronger property, but it could be formulated in a more general setting with a minimum of additional technical machinery, as it relied only on the structure of the open sets in a space.
Examples
- Examples from general topology
- Any finite topological space, including the empty set, is compact. Slightly more generally, any space with a finite topology (only finitely many open sets) is compact; this includes in particular the trivial topology.
- Any space carrying the cofinite topology is compact.
- Any locally compact Hausdorff space can be turned into a compact space by adding a single point to it, by means of Alexandroff one-point compactification. The one-point compactification of R is homeomorphic to the circle
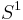 ; the one-point compactification of R2 is homeomorphic to the sphere
; the one-point compactification of R2 is homeomorphic to the sphere 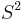 . Using the one-point compactification, one can also easily construct compact spaces which are not Hausdorff, by starting with a non-Hausdorff space.
. Using the one-point compactification, one can also easily construct compact spaces which are not Hausdorff, by starting with a non-Hausdorff space.
- The right order topology or left order topology on any bounded totally ordered set is compact. In particular, Sierpinski space is compact.
- R carrying the lower limit topology satisfies the property that no uncountable set is compact.
- In the cocountable topology on R (or any uncountable set for that matter), no infinite set is compact.
- Neither of the spaces in the previous two examples are locally compact but both are still Lindelöf
- Examples from analysis and algebra
- The closed unit interval [0, 1] is compact. This follows from the Heine–Borel theorem; the proof of which is about as hard as proving directly that [0, 1] is compact. The open interval (0, 1) is not compact: the open cover ( 1/n, 1−1/n ) for n = 3, 4, … does not have a finite subcover. Similarly, the set of rational numbers in the closed interval [0, 1] is not compact: the sets of rational numbers in the intervals
![\left[0,\frac{1}{\pi}-\frac{1}{n}\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/0bc76c341133480afe9b90224a9d9143.png) and
and ![\left[\frac{1}{\pi}+\frac{1}{n},1\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ecbc09ad9baa31d45467e7a71128f195.png) cover all the rationals in [0, 1] for n = 4, 5, … but this cover does not have a finite subcover. (Note that the sets are open in the subspace topology even though they are not open as subsets of R.)
cover all the rationals in [0, 1] for n = 4, 5, … but this cover does not have a finite subcover. (Note that the sets are open in the subspace topology even though they are not open as subsets of R.)
- The set R of all real numbers is not compact as there is a cover of open intervals that does not have a finite subcover. For example, intervals (n − 1, n + 1), where n takes all integer values in Z, cover R but there is no finite subcover.
- More generally, compact groups such as an orthogonal group are compact, while groups such as a general linear group are not.
- For every natural number n, the n-sphere is compact. Again from the Heine–Borel theorem, the closed unit ball of any finite-dimensional normed vector space is compact. This is not true for infinite dimensions; in fact, a normed vector space is finite-dimensional if and only if its closed unit ball is compact.
- On the other hand, the closed unit ball of the dual of a normed space is compact for the weak-* topology. (Alaoglu's theorem)
- The Cantor set is compact. In fact, every compact metric space is a continuous image of the Cantor set.
- Since the p-adic integers are homeomorphic to the Cantor set, they form a compact set.
- Consider the set
 of all functions
of all functions ![f: \mathbb{R} \rightarrow [0,1]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/3940de1d1e93a984f7635d770ae130bd.png) from the real number line to the closed unit interval, and define a topology on
from the real number line to the closed unit interval, and define a topology on  so that a sequence
so that a sequence 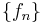 in
in  converges towards
converges towards  if and only if
if and only if 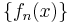 converges towards
converges towards  for all
for all  . There is only one such topology; it is called the topology of pointwise convergence. Then
. There is only one such topology; it is called the topology of pointwise convergence. Then  is a compact topological space; this follows from the Tychonoff theorem.
is a compact topological space; this follows from the Tychonoff theorem.
- Consider the set K of all functions ƒ : [0, 1] → [0, 1] satisfying the Lipschitz condition |ƒ(x) − ƒ(y)| ≤ |x − y| for all x, y ∈ [0, 1]. Consider on K the metric induced by the uniform distance
![d(f,g)=\sup\{|f(x)-g(x)| \colon x\in [0,1]\}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b99f80493f96c525c3a6b83afd88ae17.png) . Then by Arzelà–Ascoli theorem the space K is compact.
. Then by Arzelà–Ascoli theorem the space K is compact.
- The spectrum of any bounded linear operator on a Banach space is a nonempty compact subset of the complex numbers C. Conversely, any compact subset of C arises in this manner, as the spectrum of some bounded linear operator. For instance, a diagonal operator on the Hilbert space
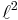 may have any compact nonempty subset of C as spectrum.
may have any compact nonempty subset of C as spectrum.
- The spectrum of any commutative ring with the Zariski topology (that is, the set of all prime ideals) is compact, but never Hausdorff (except in trivial cases). In algebraic geometry, such topological spaces are examples of quasi-compact schemes, "quasi" referring to the non-Hausdorff nature of the topology.
- The spectrum of a Boolean algebra is compact, a fact which is part of the Stone representation theorem. Stone spaces, compact totally disconnected Hausdorff spaces, form the abstract framework in which these spectra are studied. Such spaces are also useful in the study of profinite groups.
- The structure space of a commutative unital Banach algebra is a compact Hausdorff space.
- The Hilbert cube is compact, again a consequence of Tychonoff's theorem.
Theorems
Some theorems related to compactness (see the glossary of topology for the definitions):
- A continuous image of a compact space is compact.[3]
- The pre-image of a compact space under a proper map is compact.
- The extreme value theorem: a continuous real-valued function on a nonempty compact space is bounded above and attains its supremum.[4] (Slightly more generally, this is true for an upper semicontinuous function.)
- A closed subset of a compact space is compact.[5]
- A finite union of compact sets is compact.
- A nonempty compact subset of the real numbers has a greatest element and a least element.
- A subset of Euclidean n-space is compact if and only if it is closed and bounded. (Heine–Borel theorem)
- The product of any collection of compact spaces is compact. (Tychonoff's theorem, which is equivalent to the axiom of choice)
- Every topological space X is a dense subspace of a compact space having at most one point more than X, by the Alexandroff one-point compactification. By the same construction, every locally compact Hausdorff space X is a dense subspace of a compact Hausdorff space having at most one point more than X..
- Let X be a simply ordered set endowed with the order topology. Then X is compact if and only if X is a complete lattice (i.e. all subsets have suprema and infima).[6]
- Characterizations of compactness
The following are equivalent.
- A topological space X is compact.
- Any collection of closed subsets of X with the finite intersection property has nonempty intersection.
- X has a sub-base such that every cover of the space by members of the sub-base has a finite subcover (Alexander's sub-base theorem)
- Every net on X has a convergent subnet (see the article on nets for a proof).
- Every filter on X has a convergent refinement.
- Every ultrafilter on X converges to at least one point.
- Every infinite subset of X has a complete accumulation point.[7]
- Euclidean space
For any subset A of Euclidean space Rn, the following are equivalent:
- Every open cover of A has a finite subcover.
- Every sequence in A has a convergent subsequence, whose limit lies in A.
- Every infinite subset of A has at least one accumulation point in A.
- A is closed set and bounded (Heine-Borel theorem).
- A is complete and totally bounded.
In practice, the condition (4) is easiest to verify, for example a closed interval or closed n-ball.
- Metric spaces
- A metric space (or uniform space) is compact if and only if it is complete and totally bounded.[8]
- If the metric space X is compact and an open cover of X is given, then there exists a number δ > 0 such that every subset of X of diameter < δ is contained in some member of the cover. (Lebesgue's number lemma)
- Every compact metric space is separable.
- A metric space (or more generally any first-countable uniform space) is compact if and only if every sequence in the space has a convergent subsequence. (Sequentially compact)
- Hausdorff spaces
- A compact subset of a Hausdorff space is closed.[9] More generally, compact sets can be separated by open sets: if K1 and K2 are compact and disjoint, there exist disjoint open sets U1 and U2 such that
 and
and  . This is to say, compact Hausdorff space is normal.
. This is to say, compact Hausdorff space is normal. - Two compact Hausdorff spaces X1 and X2 are homeomorphic if and only if their rings of continuous real-valued functions C(X1) and C(X2) are isomorphic. (Gelfand–Naimark theorem) Properties of the Banach space of continuous functions on a compact Hausdorff space are central to abstract analysis.
- Every continuous map from a compact space to a Hausdorff space is closed and proper (i.e., the pre-image of a compact set is compact.) In particular, every continuous bijective map from a compact space to a Hausdorff space is a homeomorphism.[10]
- A topological space can be embedded in a compact Hausdorff space if and only if it is a Tychonoff space.
Other forms of compactness
There are a number of topological properties which are equivalent to compactness in metric spaces, but are inequivalent in general topological spaces. These include the following.
- Sequentially compact: Every sequence has a convergent subsequence.
- Countably compact: Every countable open cover has a finite subcover. (Or, equivalently, every infinite subset has an ω-accumulation point.)
- Pseudocompact : Every real-valued continuous function on the space is bounded.
- Limit point compact: Every infinite subset has an accumulation point.
While all these conditions are equivalent for metric spaces, in general we have the following implications:
- Compact spaces are countably compact.
- Sequentially compact spaces are countably compact.
- Countably compact spaces are pseudocompact and weakly countably compact.
Not every countably compact space is compact; an example is given by the first uncountable ordinal with the order topology. Not every compact space is sequentially compact; an example is given by 2[0,1], with the product topology (Scarborough & Stone 1966, Example 5.3).
A metric space is called pre-compact or totally bounded if any sequence has a Cauchy subsequence; this can be generalised to uniform spaces. For complete metric spaces this is equivalent to compactness. See relatively compact for the topological version.
Another related notion which (by most definitions) is strictly weaker than compactness is local compactness.
Generalizations of compactness include H-closed and the property of being an H-set in a parent space. A space is H-closed if every open cover has a finite subfamily whose union is dense. Whereas we say X is an H-set of Z if every cover of X with open sets of Z has a finite subfamily whose Z closure contains X.
See also
- Compactly generated space
- Exhaustion by compact sets
- Lindelöf space
- Metacompact space
- Noetherian space
- Orthocompact space
- Paracompact space
Notes
- ↑ Kline 1972, p. 952-953; Boyer & Merzbach 1991, p. 561
- ↑ Kline 1972, Chapter 46, §2
- ↑ Arkhangel'skii & Fedorchuk 1990, Theorem 5.2.2; See also Compactness is preserved under a continuous map on PlanetMath
- ↑ Arkhangel'skii & Fedorchuk 1990, Corollary 5.2.1
- ↑ Arkhangel'skii & Fedorchuk 1990, Theorem 5.2.3; Closed set in a compact space is compact on PlanetMath; Closed subsets of a compact set are compact on PlanetMath
- ↑ (Steen & Seebach 1995, p. 67)
- ↑ (Kelley 1955, p. 163)
- ↑ Arkhangel'skii & Fedorchuk 1990, Theorem 5.3.7
- ↑ Arkhangel'skii & Fedorchuk 1990, Theorem 5.2.4
- ↑ Arkhangel'skii & Fedorchuk 1990, Corollary 5.2.2
References
- Alexandrov, Pavel; Urysohn, Pavel (1929), "Mémoire sur les espaces topologiques compacts", Koninklijke Nederlandse Akademie van Vetenschappen te Amsterdam, Proceedings of the section of mathematical sciences 14.
- Arkhangel'skii, A.V.; Fedorchuk, V.V. (1990), "The basic concepts and constructions of general topology", in Arkhangel'skii, A.V.; Pontrjagin, L.S., General topology I, Encyclopedia of the Mathematical Sciences, 17, Springer, ISBN 9780387181783.
- Arkhangel'skii, A.V. (2001), "Compact space", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/C/c023530.htm.
- Bolzano, Bernard (1817), Rein analytischer Beweis des Lehrsatzes, dass zwischen je zwey Werthen, die ein entgegengesetzes Resultat gewähren, wenigstens eine reele Wurzel der Gleichung liege, Wilhelm Engelmann, http://books.google.com/?id=EoW4AAAAIAAJ&dq=%22Rein%20analytischer%20Beweis%20des%20Lehrsatzes%22&pg=PA2-IA3#v=onepage&q= (Purely analytic proof of the theorem that between any two values which give results of opposite sign, there lies at least one real root of the equation).
- Borel, Émile (1895), "Sur quelques points de la théorie des fonctions", Annales scientifiques de l'École Normale Supérieure, Sér. 3 12: 9–55, JFM 26.0429.03, http://www.numdam.org/numdam-bin/item?id=ASENS_1895_3_12__9_0
- Boyer, Carl B. (1959), The history of the calculus and its conceptual development, New York: Dover Publications, MR0124178.
- Arzelà, Cesare (1895), "Sulle funzioni di linee", Mem. Accad. Sci. Ist. Bologna Cl. Sci. Fis. Mat. 5 (5): 55–74.
- Arzelà, Cesare (1882–1883), "Un'osservazione intorno alle serie di funzioni", Rend. Dell' Accad. R. Delle Sci. Dell'Istituto di Bologna: 142–159.
- Ascoli, G. (1883–1884), "Le curve limiti di una varietà data di curve", Atti della R. Accad. Dei Lincei Memorie della Cl. Sci. Fis. Mat. Nat. 18 (3): 521–586.
- Fréchet, Maurice (1906), "Sur quelques points du calcul fonctionnel", Rendiconti del Circolo Matematico di Palermo 22 (1): 1–72, doi:10.1007/BF03018603.
- Kelley, John (1955), General topology, Graduate Texts in Mathematics, 27, Springer-Verlag.
- Kline, Morris (1972), Mathematical thought from ancient to modern times (3rd ed.), Oxford University Press (published 1990), ISBN 978-0-19-506136-9.
- Lebesgue, Henri (1904), Leçons sur l'intégration et la recherche des fonctions primitives, Gauthier-Villars, http://books.google.com/?id=VfUKAAAAYAAJ&dq=%22Lebesgue%22%20%22Le%C3%A7ons%20sur%20l'int%C3%A9gration%20et%20la%20recherche%20des%20fonctions%20...%22&pg=PA1#v=onepage&q=.
- Scarborough, C.T.; Stone, A.H. (1966), "Products of nearly compact spaces", Transactions of the American Mathematical Society (Transactions of the American Mathematical Society, Vol. 124, No. 1) 124 (1): 131–147, doi:10.2307/1994440, http://jstor.org/stable/1994440.
- Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978], Counterexamples in Topology (Dover reprint of 1978 ed.), Berlin, New York: Springer-Verlag, MR507446, ISBN 978-0-486-68735-3
External links
- Countably compact on PlanetMath
- A pedagogical history of compactness, Manya Raman Sundstrom, 2010
This article incorporates material from Examples of compact spaces on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.


