Biological half-life
The biological half-life or elimination half life of a substance is the time it takes for a substance (for example a metabolite, drug, signalling molecule, radioactive nuclide, or other substance) to lose half of its pharmacologic, physiologic, or radiologic activity, as per the MeSH definition. In a medical context, half-life may also describe the time it takes for the blood plasma concentration of a substance to halve ("plasma half-life") its steady-state. The relationship between the biological and plasma half-lives of a substance can be complex, due to factors including accumulation in tissues, active metabolites, and receptor interactions.[1]
Biological half-life is an important pharmacokinetic parameter and is usually denoted by the abbreviation t½.[2]
While a radioactive isotope decays perfectly according to first order kinetics where the rate constant is fixed, the elimination of a substance from a living organism follows more complex kinetics. See the article rate equation.
Contents |
Examples of biological half-lives
Water
The biological half-life of water in a human is about 7 to 14 days. It can be altered by behavior. Drinking large amounts of alcohol will reduce the biological half-life of water in the body. This has been used to decontaminate humans who are internally contaminated with tritiated water (tritium). Drinking the same amount of water would have a similar effect, but many would find it difficult to drink a large volume of water. The basis of this decontamination method (used at Harwell) is to increase the rate at which the water in the body is replaced with new water.
Alcohol
The removal of ethanol (drinking alcohol) through oxidation by alcohol dehydrogenase in the liver from the human body is limited. Hence the removal of a large concentration of alcohol from blood may follow zero-order kinetics. Also the rate-limiting steps for one substance may be in common with other substances. For instance, the blood alcohol concentration can be used to modify the biochemistry of methanol and ethylene glycol. In this way the oxidation of methanol to the toxic formaldehyde and formic acid in the (human body) can be prevented by giving an appropriate amount of ethanol to a person who has ingested methanol. Note that methanol is very toxic and causes blindness and death. A person who has ingested ethylene glycol can be treated in the same way.
Prescription medications
| Substance | Half-life | Notes |
|---|---|---|
| Amiodarone | 25 days | |
| Cisplatin | 30 to 100 h | |
| Chlorambucil | 1.53 h | |
| Digoxin | 24 to 36 h | |
| Fluoxetine | 1 to 6 days |
The active metabolite of fluoxetine is lipophilic and migrates slowly from the brain to the blood. The metabolite has a biological half-life of 4 to 16 days. |
| Methadone | 15 to 60 h, in rare cases up to 190 h.[3] | |
| Oxaliplatin | 14 min[4] | |
| Salbutamol | 1.6 h |
Metals
The biological half-life of caesium in humans is between one and four months. This can be shortened by feeding the person prussian blue. The prussian blue in the digestive system acts as a solid ion exchanger which absorbs the caesium while releasing potassium ions.
For some substances, it is important to think of the human or animal body as being made up of several parts, each with their own affinity for the substance, and each part with a different biological half-life (physiologically-based pharmacokinetic modelling). Attempts to remove a substance from the whole organism may have the effect of increasing the burden present in one part of the organism. For instance, if a person who is contaminated with lead is given EDTA in a chelation therapy, then while the rate at which lead is lost from the body will be increased, the lead within the body tends to relocate into the brain where it can do the most harm.
- Polonium in the body has a biological half-life of about 30 to 50 days.
- Caesium in the body has a biological half-life of about one to four months.
- Lead in bone has a biological half-life of about ten years.
- Cadmium in bone has a biological half-life of about 30 years.
- Plutonium in bone has a biological half-life of about 100 years.
- Plutonium in the liver has a biological half-life of about 40 years.
Rate equations
First-order elimination
There are circumstances where the half-life varies with the concentration of the drug. Thus the half-life, under these circumstances, is proportional to the initial concentration of the drug A0 and inversely proportional to the zero-order rate constant k0 where:
This process is usually a logarithmic process - that is, a constant proportion of the agent is eliminated per unit time.[5] Thus the fall in plasma concentration after the administration of a single dose is described by the following equation:
- Ct is concentration after time t
- C0 is the initial concentration (t=0)
- k is the elimination rate constant
The relationship between the elimination rate constant and half-life is given by the following equation:
Half-life is determined by clearance (CL) and volume of distribution (VD) and the relationship is described by the following equation:
In clinical practice, this means that it takes 4 to 5 times the half-life for a drug's serum concentration to reach steady state after regular dosing is started, stopped, or the dose changed. So, for example, digoxin has a half-life (or t½) of 24–36 h; this means that a change in the dose will take the best part of a week to take full effect. For this reason, drugs with a long half-life (e.g. amiodarone, elimination t½ of about 58 days) are usually started with a loading dose to achieve their desired clinical effect more quickly.
Sample values and equations
| Variable | Description | Example value | Abbreviation(s) | Formula |
|---|---|---|---|---|
| Dose | loading dose (LD), or steady state/maintenance dose (MD) | 1000 mg |  |
 |
| Volume of distribution | The apparent volume in which a drug is distributed immediately after it has been injected intravenously and equilibrated between plasma and the surrounding tissues. | 25 L | 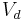 |
 |
| Concentration | initial or steady-state concentration of drug in plasma | 40.0 mg/L |  |
 |
| Biological half-life | The time required for the concentration of the drug to reach half of its original value. | 14 hr |  |
 |
| Elimination rate constant | The rate at which drugs are removed from the body. | 0.05 /hr |  |
 |
| Elimination rate | rate of infusion required to balance elimination | 50 mg/hr |  |
 |
| Area under the curve | The integral of the plasma drug concentration (Cp) after it is administered. | 0.1 mg/mL×hr |  |
 |
| Clearance | The volume of plasma cleared of the drug per unit time. | 1.25 L/hr |  |
 |
| Bioavailability | The fraction of drug that is absorbed. | 1 |  |
![= \frac{[AUC]_{oral}\div dose_{oral}}{[AUC]_{IV}\div dose_{IV}}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/68cb4d79503e0c9ed1aec2845aa018e4.png) |
| Cmax | The peak plasma concentration of a drug after oral administration. | 40.0 mg/L |  |
direct measurement |
| Cmin | The lowest (trough) concentration that a drug reaches before the next dose is administered. | 1.0 mg/L |  |
direct measurement |
| edit | ||||
See also
- Half-life, pertaining to the general mathematical concept in physics or pharmacology.
- Kinetics
- Effective half-life
References
- ↑ Lin VW; Cardenas DD (2003). Spinal cord medicine. Demos Medical Publishing, LLC. p. 251. ISBN 1888799617. http://books.google.co.uk/books?id=3anl3G4No_oC&pg=PA251&lpg=PA251&source=bl&ots=DsuJ9YCfzo&sig=5VzoJK5BqWMoMm7T3DzAKvpG_Xo&hl=en&ei=45X8SZGWAd3TjAe3pIiSAw&sa=X&oi=book_result&ct=result&resnum=5.
- ↑ IUPAC Gold Book internet edition: "biological half life".
- ↑ Manfredonia, John (March 2005). "Prescribing Methadone for Pain Management in End-of-Life Care". JAOA—The Journal of the American Osteopathic Association. http://www.jaoa.org/cgi/content/full/105/3_suppl/18S. Retrieved 2007-01-29.
- ↑ Ehrsson, Hans et al. (Winter 2002). "Pharmacokinetics of oxaliplatin in humans". Medical Oncology. http://journals.humanapress.com/index.php?option=com_opbookdetails&task=articledetails&category=humanajournals&article_code=MO:19:4:261. Retrieved 2007-03-28.
- ↑ Birkett DJ (2002). For example, ethanol may be consumed in sufficient quantity to saturate the metabolic enzymes in the liver, and so is eliminated from the body at an approximately constant rate (zero-order eliminationPharmacokinetics Made Easy (Revised Edition). Sydney: McGraw-Hill Australia. ISBN 0-07-471072-9.
|
|||||||||||||||||



