Bellman–Ford algorithm

Bellman–Ford algorithm
Class Single-source shortest path problem (for weighted directed graphs)
Data structure Graph
Worst case performance 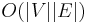O (|V| |E|)
Worst case space complexity 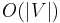O (|V|)
Graph and tree search algorithms
Search
More
Related

The Bellman–Ford algorithm computes single-source shortest paths in a weighted digraph. For graphs with only non-negative edge weights, the faster Dijkstra's algorithm also solves the problem. Thus, Bellman–Ford is used primarily for graphs with negative edge weights. The algorithm is named after its developers, Richard Bellman and Lester Ford, Jr.

If a graph contains a "negative cycle", i.e., a cycle whose edges sum to a negative value, then walks of arbitrarily low weight can be constructed, i.e., there can be no shortest path. Bellman-Ford can detect negative cycles and report their existence, but it cannot produce a correct answer if a negative cycle is reachable from the source.

According to Robert Sedgewick, "Negative weights are not merely a mathematical curiosity; [...] [they] arise in a natural way when we reduce other problems to shortest-paths problems".[1] Let G be a graph containing a "negative cycle". One NP-Complete variant of the shortest-path problem asks for the shortest path in G (containing a "negative cycle") such that no edge is repeated. Sedgewick gives a reduction from the Hamiltonian path problem to this variant of the problem.

Contents

Algorithm

Bellman–Ford is in its basic structure very similar to Dijkstra's algorithm, but instead of greedily selecting the minimum-weight node not yet processed to relax, it simply relaxes all the edges, and does this |V| − 1 times, where |V| is the number of vertices in the graph. The repetitions allow minimum distances to accurately propagate throughout the graph, since, in the absence of negative cycles, the shortest path can only visit each node at most once. Unlike the greedy approach, which depends on certain structural assumptions derived from positive weights, this straightforward approach extends to the general case.

Bellman–Ford runs in O(|V|·|E|) time, where |V| and |E| are the number of vertices and edges respectively.

procedure BellmanFord(list vertices, list edges, vertex source)
   // This implementation takes in a graph, represented as lists of vertices
   // and edges, and modifies the vertices so that their distance and
   // predecessor attributes store the shortest paths.

   // Step 1: Initialize graph
   for each vertex v in vertices:
       if v is source then v.distance := 0
       else v.distance := infinity
       v.predecessor := null
   
   // Step 2: relax edges repeatedly
   for i from 1 to size(vertices)-1:       
       for each edge uv in edges: // uv is the edge from u to v
           u := uv.source
           v := uv.destination             
           if u.distance + uv.weight < v.distance:
               v.distance := u.distance + uv.weight
               v.predecessor := u

   // Step 3: check for negative-weight cycles
   for each edge uv in edges:
       u := uv.source
       v := uv.destination
       if u.distance + uv.weight < v.distance:
           error "Graph contains a negative-weight cycle"

Proof of correctness

The correctness of the algorithm can be shown by induction. The precise statement shown by induction is:

Lemma. After i repetitions of for cycle:

Proof. For the base case of induction, consider i=0 and the moment before for cycle is executed for the first time. Then, for the source vertex, source.distance = 0, which is correct. For other vertices u, u.distance = infinity, which is also correct because there is no path from source to u with 0 edges.

For the inductive case, we first prove the first part. Consider a moment when a vertex's distance is updated by v.distance := u.distance + uv.weight. By inductive assumption, u.distance is the length of some path from source to u. Then u.distance + uv.weight is the length of the path from source to v that follows the path from source to u and then goes to v.

For the second part, consider the shortest path from source to u with at most i edges. Let v be the last vertex before u on this path. Then, the part of the path from source to v is the shortest path from source to v with at most i-1 edges. By inductive assumption, v.distance after i-1 cycles is at most the length of this path. Therefore, uv.weight + v.distance is at most the length of the path from s to u. In the ith cycle, u.distance gets compared with uv.weight + v.distance, and is set equal to it if uv.weight + v.distance was smaller. Therefore, after i cycles, u.distance is at most the length of the shortest path from source to u that uses at most i edges.

If there are no negative-weight cycles, then every shortest path visits each vertex at most once, so at step 3 no further improvements can be made. Conversely, suppose no improvement can be made. Then for any cycle with vertices v[0],..,v[k-1],

v[i].distance <= v[i-1 (mod k)].distance + v[i-1 (mod k)]v[i].weight

Summing around the cycle, the v[i].distance terms and the v[i-1 (mod k)] distance terms cancel, leaving

0 <= sum from 1 to k of v[i-1 (mod k)]v[i].weight

I.e., every cycle has nonnegative weight.

Applications in routing

A distributed variant of the Bellman–Ford algorithm is used in distance-vector routing protocols, for example the Routing Information Protocol (RIP). The algorithm is distributed because it involves a number of nodes (routers) within an Autonomous system, a collection of IP networks typically owned by an ISP. It consists of the following steps:

  1. Each node calculates the distances between itself and all other nodes within the AS and stores this information as a table.
  2. Each node sends its table to all neighboring nodes.
  3. When a node receives distance tables from its neighbors, it calculates the shortest routes to all other nodes and updates its own table to reflect any changes.

The main disadvantages of the Bellman–Ford algorithm in this setting are as follows:

Yen's improvement

In a 1970 publication, Yen[2] described an improvement to the Bellman–Ford algorithm for a graph without negative-weight cycles. Yen's improvement first assigns some arbitrary linear order on all vertices and then partitions the set of all edges into one of two subsets. The first subset, Ef, contains all edges (vi, vj) such that i < j; the second, Eb, contains edges (vi, vj) such that i > j. Each vertex is visited in the order v1, v2,...,v|V|, relaxing each outgoing edge from that vertex in Ef. Each vertex is then visited in the order v|V|, v|V|-1,...,v1, relaxing each outgoing edge from that vertex in Eb. Yen's improvement effectively halves the number of "passes" required for the single-source-shortest-path solution.

Notes

  1. ↑ Robert Sedgewick. Algorithms in Java. Third Edition. ISBN 0-201-36121-3. Section 21.7: Negative Edge Weights. http://safari.oreilly.com/0201361213/ch21lev1sec7
  2. ↑ Jin Y. Yen. "An algorithm for Finding Shortest Routes from all Source Nodes to a Given Destination in General Network", Quart. Appl. Math., 27, 1970, 526–530.

References

External links