Hexadecimal
| Numeral systems by culture | |
|---|---|
| Hindu-Arabic numerals | |
| Western Arabic Eastern Arabic Indian family Burmese |
Khmer Mongolian Thai |
| East Asian numerals | |
| Chinese Japanese Suzhou |
Korean Vietnamese Counting rods |
| Alphabetic numerals | |
| Abjad Armenian Āryabhaṭa Cyrillic |
Ge'ez Greek (Ionian) Hebrew |
| Other systems | |
| Aegean Attic Babylonian Brahmi Egyptian Etruscan |
Inuit Mayan Quipu Roman Sumerian Urnfield |
| List of numeral system topics | |
| Positional systems by base | |
| Decimal (10) | |
| 1, 2, 3, 4, 5, 6, 8, 12, 16, 20, 30, 36, 60 more… | |
In mathematics and computer science, hexadecimal (also base 16, or hex) is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F (or alternatively a through f) to represent values ten to fifteen. For example, the hexadecimal number 2AF3 is equal, in decimal, to (2 × 163) + (10 × 162) + (15 × 161) + (3 × 160) , or 10,995.
Each hexadecimal digit represents four binary digits (bits) (also called a "nibble"), and the primary use of hexadecimal notation is as a human-friendly representation of binary coded values in computing and digital electronics. For example, byte values can range from 0 to 255 (decimal) but may be more conveniently represented as two hexadecimal digits in the range 00 through FF. Hexadecimal is also commonly used to represent computer memory addresses.
Contents |
Representing hexadecimal
| 0hex | = | 0dec | = | 0oct | 0 | 0 | 0 | 0 | |||
| 1hex | = | 1dec | = | 1oct | 0 | 0 | 0 | 1 | |||
| 2hex | = | 2dec | = | 2oct | 0 | 0 | 1 | 0 | |||
| 3hex | = | 3dec | = | 3oct | 0 | 0 | 1 | 1 | |||
| 4hex | = | 4dec | = | 4oct | 0 | 1 | 0 | 0 | |||
| 5hex | = | 5dec | = | 5oct | 0 | 1 | 0 | 1 | |||
| 6hex | = | 6dec | = | 6oct | 0 | 1 | 1 | 0 | |||
| 7hex | = | 7dec | = | 7oct | 0 | 1 | 1 | 1 | |||
| 8hex | = | 8dec | = | 10oct | 1 | 0 | 0 | 0 | |||
| 9hex | = | 9dec | = | 11oct | 1 | 0 | 0 | 1 | |||
| Ahex | = | 10dec | = | 12oct | 1 | 0 | 1 | 0 | |||
| Bhex | = | 11dec | = | 13oct | 1 | 0 | 1 | 1 | |||
| Chex | = | 12dec | = | 14oct | 1 | 1 | 0 | 0 | |||
| Dhex | = | 13dec | = | 15oct | 1 | 1 | 0 | 1 | |||
| Ehex | = | 14dec | = | 16oct | 1 | 1 | 1 | 0 | |||
| Fhex | = | 15dec | = | 17oct | 1 | 1 | 1 | 1 | |||
In situations where there is no context, a hexadecimal number might be ambiguous and confused with numbers expressed in other bases. There are several conventions for expressing values unambiguously. A numerical subscript (itself written in decimal) can give the base explicitly: 15910 is decimal 159; 15916 is hexadecimal 159, which is equal to 34510. Other authors prefer a text subscript, such as 159decimal and 159hex, or 159d and 159h.
In linear text systems, such as those used in most computer programming environments, a variety of methods have arisen:
- In URLs, character codes are written as hexadecimal pairs prefixed with
%:http://www.example.com/name%20with%20spaceswhere%20is the space (blank) character (code value 20 in hex, 32 in decimal). - In XML and XHTML, characters can be expressed as hexadecimal numeric character references using the notation
ode;, where code is the 1- to 6-digit hex number assigned to the character in the Unicode standard. Thus’represents the curled right single quote (Unicode value 2019 in hex, 8217 in decimal). - Color references in HTML and CSS can be expressed with six hexdigits (two each for the red, green, and blue components, in that order) prefixed with
#: white, for example, is represented#FFFFFF.[1] CSS allows 3-hexdigit abbreviations with one hexdigit per component: #FA3 abbreviates #FFAA33 (a golden orange). - *nix (Unix and related) shells, and likewise the C programming language, which was designed for Unix (and the syntactic descendants of C[2]) use the prefix
0xfor numeric constants represented in hex:0x5A3. Character and string constants may express character codes in hexadecimal with the prefix\xfollowed by two hex digits:'\x1B'represents the Esc control character;"\x1B[0m\x1B[25;1H"is a string containing 11 characters (plus a trailing NUL to mark the end of the string) with two embedded Esc characters.[3] To output an integer as hexadecimal with the printf function family, the format conversion code%Xor%xis used. - In the Unicode standard, a character value is represented with
U+followed by the hex value:U+20ACis the Euro sign (€). - In MIME (e-mail extensions) quoted-printable encoding, characters that cannot be represented as literal ASCII characters are represented by their codes as two hexadecimal digits (in ASCII) prefixed by an equal to sign
=, as inEspa=F1ato send "España" (Spain). (Hexadecimal F1, equal to decimal 241, is the code number for the lower case n with tilde in the ISO/IEC 8859-1 character set.) - In Intel-derived assembly languages, hexadecimal is indicated with a suffixed H or h:
FFhor05A3H. Some implementations require a leading zero when the first hexadecimal digit character is not a decimal digit:0FFh - Other assembly languages (6502, AT&T, Motorola), Pascal, Delphi, some versions of BASIC (Commodore) and Forth use
$as a prefix:$5A3. - Some assembly languages (Microchip) use the notation
H'ABCD'(for ABCD16). - Ada and VHDL enclose hexadecimal numerals in based "numeric quotes":
16#5A3#. VHDL also supportsx"5A3". - Verilog represents hexadecimal constants in the form
8'hFF, where 8 is the number of bits in the value and FF is the hexadecimal constant. - Modula-2 and some other languages use # as a prefix:
#05A3 - The Smalltalk programming language uses the prefix
16r:16r5A3 - Postscript indicates hex with prefix
16#:16#5A3. Binary data (such as image pixels) can be expressed as unprefixed consecutive hexadecimal pairs:AA213FD51B3801043FBC... - In early systems when a Macintosh crashed, one or two lines of hexadecimal code would be displayed under the Sad Mac to tell the user what went wrong.
- Common Lisp use the prefixes
#xand#16r. - QuickBASIC, FreeBASIC and Visual Basic prefix hexadecimal numbers with
&H:&H5A3 - BBC BASIC and Locomotive BASIC use
&for hex.[4] - TI-89 and 92 series uses a
0hprefix:0h5A3 - Notations such as
X'5A3'are sometimes seen, such as in PL/I. This is the most common format for hexadecimal on IBM mainframes (zSeries) and midrange computers (iSeries) running traditional OS's (zOS, zVSE, zVM, TPF, OS/400), and is used in Assembler, PL/1, Cobol, JCL, scripts, commands and other places. This format was common on other (and now obsolete) IBM systems as well. - Donald Knuth introduced the use of a particular typeface to represent a particular radix in his book The TeXbook.[5] Hexadecimal representations are written there in a typewriter typeface: 5A3
- Any IPv6 address can be written as eight groups of four hexadecimal digits, where each group is separated by a colon (
:). This, for example, is a valid IPv6 address: 2001:0db8:85a3:0000:0000:8a2e:0370:7334

There is no universal convention to use lowercase or uppercase for the letter digits, and each is prevalent or preferred in particular environments by community standards or convention.
The choice of the letters A through F to represent the digits above nine was not universal in the early history of computers. During the 1950s, some installations favored using the digits 0 through 5 with a macron character ("¯") to indicate the values 10–15. Users of Bendix G-15 computers used the letters U through Z. Bruce A. Martin of Brookhaven National Laboratory considered the choice of A–F "ridiculous" and in a 1968 letter to the editor of the CACM proposed an entirely new set of symbols based on the bit locations, which did not gain much acceptance.[6]
Verbal and digital representations
There are no traditional numerals to represent the quantities from ten to fifteen—letters are used as a substitute—and most Western European languages lack non-decimal names for the numerals above ten. Even though English has names for several non-decimal powers (pair for the first binary power, score for the first vigesimal power, dozen, gross, and great gross for the first three duodecimal powers), no English name describes the hexadecimal powers (decimal 16, 256, 4096, 65536, ... ). Some people read hexadecimal numbers digit by digit like a phone number: 4DA is "four-dee-ay". However, the letter A sounds like "eight", C sounds like "three", and D can easily be mistaken for the "-ty" suffix: Is it 4D or forty? Other people avoid confusion by using the NATO phonetic alphabet: 4DA is "four-delta-alfa"; or the Joint Army/Navy Phonetic Alphabet ("four-dog-able"); or a similar ad hoc system.

Systems of counting on digits have been devised for both binary and hexadecimal. Arthur C. Clarke suggested using each finger as an on/off bit, allowing finger counting from zero to 1023 on ten fingers. Another system for counting up to FF (255) is illustrated on the right; it seems to be an extension of an existing system for counting in twelves (dozens and grosses), that is common in South Asia and elsewhere.
Signs
The hexadecimal system can express negative numbers the same way as in decimal: –2A to represent –42 and so on.
However, some prefer instead to express the exact bit patterns used in the processor and consider hexadecimal values best handled as signed values. This way, the negative number –42 can be written as FFFF FFD6 in a 32-bit CPU register, as C228 0000 in a 32-bit FPU register or C045 0000 0000 0000 in a 64-bit FPU register (assuming certain representation schemes, two's-complement in the 32-bit non-FPU instance and sign-magnitude in the FPU instances.)
Binary conversion
Most computers manipulate binary data, but it is difficult for humans to work with the large number of digits for even a relatively small binary number. Although most humans are familiar with the base 10 system, it is much easier to map binary to hexadecimal than to decimal because each hexadecimal digit maps to a whole number of bits (410). This example converts 11112 to base ten. Since each position in a binary numeral can contain either a 1 or 0, its value may be easily determined by its position from the right:
- 00012 = 110
- 00102 = 210
- 01002 = 410
- 10002 = 810
Therefore:
| 11112 | = 810 + 410 + 210 + 110 |
| = 1510 |
With surprisingly little practice, mapping 11112 to F16 in one step becomes easy: see table in Representing hexadecimal. The advantage of using hexadecimal rather than decimal increases rapidly with the size of the number. When the number becomes large, conversion to decimal is very tedious. However, when mapping to hexadecimal, it is trivial to regard the binary string as 4-digit groups and map each to a single hexadecimal digit.
This example shows the conversion of a binary number to decimal, mapping each digit to the decimal value, and adding the results.
| 010111101011010100102 | = 26214410 + 6553610 + 3276810 + 1638410 + 819210 + 204810 + 51210 + 25610 + 6410 + 1610 + 210 |
| = 38792210 |
Compare this to the conversion to hexadecimal, where each group of four digits can be considered independently, and converted directly:
| 010111101011010100102 | = | 0101 | 1110 | 1011 | 0101 | 00102 |
| = | 5 | E | B | 5 | 216 | |
| = | 5EB5216 | |||||
The conversion from hexadecimal to binary is equally direct.
The octal system can also be useful as a tool for people who need to deal directly with binary computer data. Octal represents data as three bits per character, rather than four.
Converting from other bases
Division-remainder in source base
As with all bases there is a simple algorithm for converting a representation of a number to hexadecimal by doing integer division and remainder operations in the source base. Theoretically this is possible from any base but for most humans only decimal and for most computers only binary (which can be converted by far more efficient methods) can be easily handled with this method.
Let d be the number to represent in hexadecimal, and the series hihi-1...h2h1 be the hexadecimal digits representing the number.
- i := 1
- hi := d mod 16
- d := (d-hi) / 16
- If d = 0 (return series hi) else increment i and go to step 2
"16" may be replaced with any other base that may be desired.
The following is a JavaScript implementation of the above algorithm for converting any number to a hexadecimal in String representation. Its purpose is to illustrate the above algorithm. To work with data seriously however, it is much more advisable to work with bitwise operators.
function toHex(d) { var r = d % 16; var result; if (d-r == 0) result = toChar(r); else result = toHex( (d-r)/16 ) + toChar(r); return result; } function toChar(n) { const alpha = "0123456789ABCDEF"; return alpha.charAt(n); }
Addition and multiplication

It is also possible to make the conversion by assigning each place in the source base the hexadecimal representation of its place value and then performing multiplication and addition to get the final representation. I.e. to convert the number B3AD to decimal one can split the conversion into D (1310), A (1010), 3 (310) and B (1110) then get the final result by multiplying each decimal representation by 16p, where 'p' is the corresponding position from right to left, beginning with 0. In this case we have 13*(160) + 10*(161) + 3*(162) + 11*(163), which is equal 45997 in the decimal system.
Tools for conversion
Most modern computer systems with graphical user interfaces provide a built-in calculator utility, capable of performing conversions between various radixes, generally including hexadecimal.
In Microsoft Windows, the Calculator utility can be set to Scientific mode (called Programmer mode in some versions), which allows conversions between radix 16 (hexadecimal), 10 (decimal), 8 (octal) and 2 (binary); the bases most commonly used by programmers. In Scientific Mode, the on-screen numeric keypad includes the hexadecimal digits A through F which are active when "Hex" is selected. In hex mode, however, the Windows Calculator only supports integers.
Real numbers
As with other numeral systems, the hexadecimal system can be used to represent rational numbers, although recurring digits are common since sixteen (10h) has only a single prime factor (two):
| ½ |
|
0.8 | ⅙ |
|
0.2A | 1⁄A |
|
0.19 | 1⁄E |
|
0.1249 |
| ⅓ |
|
0.5 | 1⁄7 |
|
0.249 | 1⁄B |
|
0.1745D | 1⁄F |
|
0.1 |
| ¼ |
|
0.4 | ⅛ |
|
0.2 | 1⁄C |
|
0.15 | 1⁄10 |
|
0.1 |
| ⅕ |
|
0.3 | 1⁄9 |
|
0.1C7 | 1⁄D |
|
0.13B | 1⁄11 |
|
0.0F |
where an overline indicates a recurring pattern.
For any base, 0.1 (or "1/10") is always equivalent to one divided by the representation of that base value in its own number system: Counting in base 3 is 0, 1, 2, 10 (three). Thus, whether dividing one by two for binary or dividing one by sixteen for hexadecimal, both of these fractions are written as 0.1. Because the radix 16 is a perfect square (4²), fractions expressed in hexadecimal have an odd period much more often than decimal ones, and there are no cyclic numbers (other than trivial single digits). Recurring digits are exhibited when the denominator in lowest terms has a prime factor not found in the radix; thus, when using hexadecimal notation, all fractions with denominators that are not a power of two result in an infinite string of recurring digits (such as thirds and fifths). This makes hexadecimal (and binary) less convenient than decimal for representing rational numbers since a larger proportion lie outside its range of finite representation.
All rational numbers finitely representable in hexadecimal are also finitely representable in decimal, duodecimal and sexagesimal: that is, any hexadecimal number with a finite number of digits has a finite number of digits when expressed in those other bases. Conversely, only a fraction of those finitely representable in the latter bases are finitely representable in hexadecimal. For example, decimal 0.1 corresponds to the infinite recurring representation 0.199999999999... in hexadecimal. However, hexadecimal is more efficient than bases 12 and 60 for representing fractions with powers of two in the denominator (e.g., decimal one sixteenth is 0.1 in hexadecimal, 0.09 in duodecimal, 0;3,45 in sexagesimal and 0.0625 in decimal).
| In decimal Prime factors of the base: 2, 5 |
In hexadecimal Prime factors of the base: 2 |
||||
| Fraction | Prime factors of the denominator |
Positional representation | Positional representation | Prime factors of the denominator |
Fraction |
| 1/2 | 2 | 0.5 | 0.8 | 2 | 1/2 |
| 1/3 | 3 | 0.3333... = 0.3 | 0.5555... = 0.5 | 3 | 1/3 |
| 1/4 | 2 | 0.25 | 0.4 | 2 | 1/4 |
| 1/5 | 5 | 0.2 | 0.3 | 5 | 1/5 |
| 1/6 | 2, 3 | 0.16 | 0.2A | 2, 3 | 1/6 |
| 1/7 | 7 | 0.142857 | 0.249 | 7 | 1/7 |
| 1/8 | 2 | 0.125 | 0.2 | 2 | 1/8 |
| 1/9 | 3 | 0.1 | 0.1C7 | 3 | 1/9 |
| 1/10 | 2, 5 | 0.1 | 0.19 | 2, 5 | 1/A |
| 1/11 | 11 | 0.09 | 0.1745D | B | 1/B |
| 1/12 | 2, 3 | 0.083 | 0.15 | 2, 3 | 1/C |
| 1/13 | 13 | 0.076923 | 0.13B | D | 1/D |
| 1/14 | 2, 7 | 0.0714285 | 0.1249 | 2, 7 | 1/E |
| 1/15 | 3, 5 | 0.06 | 0.1 | 3, 5 | 1/F |
| 1/16 | 2 | 0.0625 | 0.1 | 2 | 1/10 |
| 1/17 | 17 | 0.0588235294117647 | 0.0F | 11 | 1/11 |
| 1/18 | 2, 3 | 0.05 | 0.0E38 | 2, 3 | 1/12 |
| 1/19 | 19 | 0.052631578947368421 | 0.0D79435E50 | 13 | 1/13 |
| 1/20 | 2, 5 | 0.05 | 0.0C | 2, 5 | 1/14 |
| 1/21 | 3, 7 | 0.047619 | 0.0C3 | 3, 7 | 1/15 |
| 1/22 | 2, 11 | 0.045 | 0.0BA2E8 | 2, B | 1/16 |
| 1/23 | 23 | 0.0434782608695652173913 | 0.0B21642C8590 | 17 | 1/17 |
| 1/24 | 2, 3 | 0.0416 | 0.0A | 2, 3 | 1/18 |
| 1/25 | 5 | 0.04 | 0.0A3D70 | 5 | 1/19 |
| 1/26 | 2, 13 | 0.0384615 | 0.09D8 | 2, B | 1/1A |
| 1/27 | 3 | 0.037 | 0.097B425ED | 3 | 1/1B |
| 1/28 | 2, 7 | 0.03571428 | 0.0924 | 2, 7 | 1/1C |
| 1/29 | 29 | 0.0344827586206896551724137931 | 0.08D3DCB | 1D | 1/1D |
| 1/30 | 2, 3, 5 | 0.03 | 0.08 | 2, 3, 5 | 1/1E |
| 1/31 | 31 | 0.032258064516129 | 0.08421 | 1F | 1/1F |
| 1/32 | 2 | 0.03125 | 0.08 | 2 | 1/20 |
| 1/33 | 3, 11 | 0.03 | 0.07C1F | 3, B | 1/21 |
| 1/34 | 2, 17 | 0.02941176470588235 | 0.078 | 2, 11 | 1/22 |
| 1/35 | 5, 7 | 0.0285714 | 0.075 | 5, 7 | 1/23 |
| 1/36 | 2, 3 | 0.027 | 0.071C | 2, 3 | 1/24 |
| Algebraic irrational number | In decimal | In hexadecimal |
| √2 (the length of the diagonal of a unit square) | 1.41421356237309... | 1.6A09E667F3BCD... |
| √3 (the length of the diagonal of a unit cube) | 1.73205080756887... | 1.BB67AE8584CAA... |
| √5 (the length of the diagonal of a 1×2 rectangle) | 2.2360679774997... | 2.3C6EF372FE95... |
φ (phi, the golden ratio =
|
1.6180339887498... | 1.9E3779B97F4A... |
| Transcendental irrational number | ||
| π (pi, the ratio of circumference to diameter) | 3.1415926535897932384626433 8327950288419716939937510... |
3.243F6A8885A308D313198A2E0 3707344A4093822299F31D008... |
| e (the base of the natural logarithm) | 2.7182818284590452... | 2.B7E151628AED2A6B... |
| τ (the Thue–Morse constant) | 0.412454033640... | 0.6996 9669 9669 6996 ... |
| Number | ||
| γ (the limiting difference between the harmonic series and the natural logarithm) | 0.5772156649015328606... | 0.93C467E37DB0C7A4D1B... |
Powers
Possibly the most widely used powers, powers of two, are easier to show using base 16. The first sixteen powers of two are shown below.
| 2x | value |
|---|---|
| 20 | 1 |
| 21 | 2 |
| 22 | 4 |
| 23 | 8 |
| 24 | 10hex |
| 25 | 20hex |
| 26 | 40hex |
| 27 | 80hex |
| 28 | 100hex |
| 29 | 200hex |
2A (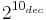 ) ) |
400hex |
2B (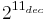 ) ) |
800hex |
2C (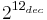 ) ) |
1000hex |
2D ( ) ) |
2000hex |
2E (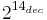 ) ) |
4000hex |
2F ( ) ) |
8000hex |
210 ( ) ) |
10000hex |
Since four squared is sixteen, powers of four have an even easier relation:
| 4x | value |
|---|---|
| 40 | 1 |
| 41 | 4 |
| 42 | 10hex |
| 43 | 40hex |
| 44 | 100hex |
| 45 | 400hex |
| 46 | 1000hex |
| 47 | 4000hex |
| 48 | 10000hex |
This also makes tetration easier when using two and four since:
32 = 24 = 10hex,
42 = 216 = 10000hex and
52 = 265536 = (1 followed by 16384 zeros)hex.
Cultural
Etymology
The word hexadecimal is composed of hexa-, derived from the Greek έξ (hex) for "six", and -decimal, derived from the Latin for "tenth". Webster's Third New International online derives "hexadecimal" as an alteration of the all-Latin "sexadecimal" (which appears in the earlier Bendix documentation). The earliest date attested for "hexadecimal" in Merriam-Webster Collegiate online is 1954, placing it safely in the category of international scientific vocabulary (ISV). It is common in ISV to mix Greek and Latin combining forms freely. The word "sexagesimal" (for base 60) retains the Latin prefix. Donald Knuth has pointed out that the etymologically correct term is "senidenary", from the Latin term for "grouped by 16". (The terms "binary", "ternary" and "quaternary" are from the same Latin construction, and the etymologically correct term for "decimal" arithmetic is "denary".)[7] Schwartzman notes that the expected form from usual Latin phrasing would be "sexadecimal", but computer hackers would be tempted to shorten that word to "sex".[8] The etymologically proper Greek term would be hexadecadic (although in Modern Greek deca-hexadic (δεκαεξαδικός) is more commonly used).
Common patterns and humor
Hexadecimal is sometimes used in programmer jokes because certain words can be formed using only hexadecimal digits. Some of these words are "dead", "beef", "babe", and with appropriate substitutions "c0ffee". Since these are quickly recognizable by programmers, debugging setups sometimes initialize memory to them to help programmers see when something has not been initialized. Some people add an H after a number if they want to show that it is written in hexadecimal. In older Intel assembly syntax, this is sometimes the case.
An example is the magic number in Universal Mach-O files and java class file structure, which is "CAFEBABE". Single-architecture 32-bit big-endian Mach-O files have the magic number "FEEDFACE" at their beginning. "DEADBEEF" is sometimes put into uninitialized memory. Microsoft Windows XP clears its locked index.dat files with the hex codes: "0BADF00D". The Visual C++ remote debugger uses "BADCAB1E" to denote a broken link to the target system.
Two common bit patterns often employed to test hardware are 01010101 and 10101010 (their corresponding hex values are 55h and AAh, respectively). The reason for their use is to alternate between off ('0') to on ('1') or vice versa when switching between these two patterns. These two values are often used together as signatures in critical PC system sectors (e.g., the hex word, 0xAA55 which on little-endian systems is 55h followed by AAh, must be at the end of a valid Master Boot Record).
The following table shows a joke in hexadecimal:
3x12=36 2x12=24 1x12=12 0x12=18
The first three are interpreted as multiplication, but in the last, "0x" signals Hexadecimal interpretation of 12, which is 18.
Another joke based on the use of a word containing only letters from the first six in the alphabet (and thus those used in hexadecimal) is...
- If only dead people understand hexadecimal, how many people understand hexadecimal?
In this case, "dead" refers to a hexadecimal number DEAD (57005 base 10), as opposed to the state of not being alive.
A Knuth reward check is one hexadecimal dollar, or $2.56.
Primary numeral system
Similar to dozenal advocacy, there have been occasional attempts to promote hexadecimal as the preferred numeral system. These attempts usually propose pronunciation and/or symbology.[9] Sometimes the proposal unifies standard measures so that they are multiples of 16.[10][11][12]
An example of unifying standard measures is Hexadecimal time which subdivides a day by 16 so that there are 16 "hexhours" in a day.[12]
Key to number base notation
Simple key for notations used in article:
| Full Text Notation | Abbreviation | Number Base |
|---|---|---|
| binary | bin | 2 |
| octal | oct | 8 |
| decimal | dec | 10 |
| hexadecimal | hex | 16 |
See also
- Base32 (content encoding scheme)
- Base64 (content encoding scheme)
- Binary numeral system
- Hex editor
- Hexdump
- Hexadecimal time
- Hexspeak
- HTML
- Nibble — one hexadecimal digit can exactly represent one "nibble"
- Numeral system — a list of other base systems
- Web colours
References
- ↑ "Hexadecimal web colors explained". http://www.web-colors-explained.com/hex.php.
- ↑ Some of C's syntactic descendants are C++, C#, Java, JavaScript, and Windows PowerShell
- ↑ The string
"\x1B[0m\x1B[25;1H"specifies the character sequence Esc [ 0 m Esc [ 2 5 ; 1 H Nul. These are the escape sequences used on an ANSI terminal that reset the character set and color, and then move the cursor to line 25. - ↑ BBC BASIC programs are not fully portable to Microsoft BASIC (without modification) since the latter takes
&to prefix octal values. (Microsoft BASIC primarily uses&Oto prefix octal, and it uses&Hto prefix hexadecimal, but the ampersand alone yields a default interpretation as an octal prefix. - ↑ Donald E. Knuth. The TeXbook (Computers and Typesetting, Volume A). Reading, Massachusetts: Addison-Wesley, 1984. ISBN 0-201-13448-9. The source code of the book in TeX (and a required set of macros CTAN.org) is available online on CTAN.
- ↑ Letters to the editor: On binary notation, Bruce A. Martin, Associated Universities Inc., Communications of the ACM, Volume 11, Issue 10 (October 1968) Page: 658 doi:10.1145/364096.364107
- ↑ Knuth, Donald. (1969). Donald Knuth, in The Art of Computer Programming, Volume 2. ISBN 0-201-03802-1. (Chapter 17.)
- ↑ Schwartzman, S. (1994). The Words of Mathematics: an etymological dictionary of mathematical terms used in English. ISBN 0-88385-511-9.
- ↑ "Base 4^2 Hexadecimal Symbol Proposal". http://www.hauptmech.com/base42.
- ↑ "Intuitor Hex Headquarters". http://www.intuitor.com/hex/.
- ↑ "A proposal for addition of the six Hexadecimal digits (A-F) to Unicode". http://std.dkuug.dk/jtc1/sc2/wg2/docs/n2677.
- ↑ 12.0 12.1 Nystrom, John William (1862). Project of a New System of Arithmetic, Weight, Measure and Coins: Proposed to be called the Tonal System, with Sixteen to the Base. Philadelphia. http://books.google.com/books?id=aNYGAAAAYAAJ.