Apsis
.png)
An apsis, plural apsides (pronounced /ˈæpsɨdiːz/), is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system. Historically, in geocentric systems, apsides were measured from the center of the Earth.
The point of closest approach (the point at which two bodies are the closest) is called the periapsis or pericentre, from Greek περὶ, peri, around. The point of farthest excursion is called the apoapsis (ἀπό, apó, "from", which becomes ἀπ-, ap- or ἀφ-, aph- before an unaspirated or aspirated vowel, respectively), apocentre or apapsis (the latter term, although etymologically more correct, is much less used). A straight line drawn through the periapsis and apoapsis is the line of apsides. This is the major axis of the ellipse, the line through the longest part of the ellipse.
Derivative terms are used to identify the body being orbited. The most common are perigee and apogee, referring to orbits around the Earth (Greek γῆ, gê, "earth"), and perihelion and aphelion, referring to orbits around the Sun (Greek ἥλιος, hēlios, "sun"). During the Apollo program, the terms pericynthion and apocynthion were used when referring to the moon.[1]
Contents |
Formula

These formulae characterize the periapsis and apoapsis of an orbit:
- Periapsis: maximum speed
 at minimum (periapsis) distance
at minimum (periapsis) distance 
- Apoapsis: minimum speed
 at maximum (apoapsis) distance
at maximum (apoapsis) distance 
while, in accordance with Kepler's laws of planetary motion (conservation of angular momentum) and the conservation of energy, these quantities are constant for a given orbit:
- specific relative angular momentum

- specific orbital energy

where:
 is the semi-major axis
is the semi-major axis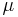 is the standard gravitational parameter
is the standard gravitational parameter is the eccentricity, defined as
is the eccentricity, defined as 
Note that for conversion from heights above the surface to distances between an orbit and its primary, the radius of the central body has to be added, and conversely.
The arithmetic mean of the two limiting distances is the length of the semi-major axis 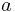 . The geometric mean of the two distances is the length of the semi-minor axis
. The geometric mean of the two distances is the length of the semi-minor axis  .
.
The geometric means of the two limiting speeds is  , the speed corresponding to a kinetic energy which, at any position of the orbit, added to the existing kinetic energy, would allow the orbiting body to escape (the square root of the product of the two speeds is the local escape velocity).
, the speed corresponding to a kinetic energy which, at any position of the orbit, added to the existing kinetic energy, would allow the orbiting body to escape (the square root of the product of the two speeds is the local escape velocity).
Terminology
The words "pericenter" and "apocenter" are occasionally seen, although periapsis/apoapsis are preferred in technical usage.
Various related terms are used for other celestial objects. The '-gee', '-helion' and '-astron' and '-galacticon' forms are frequently used in the astronomical literature, while the other listed forms are occasionally used, although '-saturnium' has very rarely been used in the last 50 years. The '-gee' form is commonly (although incorrectly) used as a generic 'closest approach to planet' term instead of specifically applying to the Earth. The term peri/apomelasma (from the Greek root) was used by physicist Geoffrey A. Landis in 1998 before peri/aponigricon (from the Latin) appeared in the scientific literature in 2002.[2]
| Body | Closest approach | Farthest approach |
|---|---|---|
| General | Periapsis/Pericentre | Apoapsis |
| Galaxy | Perigalacticon | Apogalacticon |
| Star | Periastron | Apastron |
| Black hole | Perimelasma/Peribothra/Perinigricon | Apomelasma/Apobothra/Aponigricon |
| Sun | Perihelion | Aphelion[3] |
| Mercury | Perihermion | Apohermion |
| Venus | Pericytherion/Pericytherean/Perikrition | Apocytherion/Apocytherean/Apokrition |
| Earth | Perigee | Apogee |
| Moon | Periselene/Pericynthion/Perilune | Aposelene/Apocynthion/Apolune |
| Mars | Periareion | Apoareion |
| Jupiter | Perizene/Perijove | Apozene/Apojove |
| Saturn | Perikrone/Perisaturnium | Apokrone/Aposaturnium |
| Uranus | Periuranion | Apouranion |
| Neptune | Periposeidion | Apoposeidion |
| Pluto | Perihadion | Apohadion |
Since "peri" and "apo" are Greek, it is considered by some purists[4] more correct to use the Greek form for the body, giving forms such as '-zene' for Jupiter and '-krone' for Saturn. The daunting prospect of having to maintain a different word for every orbitable body in the solar system (and beyond) is the main reason why the generic '-apsis' has become the almost universal norm.
- In the Moon's case, in practice all three forms are used, albeit very infrequently. The '-cynthion' form is, according to some, reserved for artificial bodies, whilst others reserve '-lune' for an object launched from the Moon and '-cynthion' for an object launched from elsewhere. The '-cynthion' form was the version used in the Apollo Project, following a NASA decision in 1964.
- For Venus, the form '-cytherion' is derived from the commonly used adjective 'cytherean'; the alternate form '-krition' (from Kritias, an older name for Aphrodite) has also been suggested.
- For Jupiter, the '-jove' form is occasionally used by astronomers whilst the '-zene' form is never used, like the other pure Greek forms ('-areion' (Mars), '-hermion' (Mercury), '-krone' (Saturn), '-uranion' (Uranus), '-poseidion' (Neptune) and '-hadion' (Pluto)).
Earth's perihelion and aphelion
For the Earth's orbit around the sun, the time of apsis is most relevantly expressed in terms of a time relative to seasons, as that determines the contribution of the elliptic orbit to seasonal variations; especially in insolation at the top of the atmosphere. This mechanism is primarily controlled by the annual cycle of the declination of the sun, a consequence of the tilt of the Earth's rotation axis relative to the plane of the orbit. Currently, perihelion occurs about 14 days after the December solstice, thus making January 4 the mean date of perihelion. January's perihelion puts Earth at a distance of 91,402,505 miles (147,098,074 km, 0.98328989 AU) from the Sun and July's aphelion is at 94,509,130 miles (152,097,701 km, 1.01671033 AU).
The dates of perihelion and aphelion progress through the seasons, making one complete cycle in 22,000 to 26,000 years. This is a mechanism behind one of the many Milankovitch cycles, but represents an insufficient period to cause the ice ages which occur on a period of approximately 100,000 years.
A common convention is to express the timing of perihelion relative to the vernal equinox not in days, but as an angle of orbital displacement, a longitude of the periapsis. For Earth's orbit, this would be a longitude of perihelion, which in 2000 was 282.895 degrees.[5]
The day and time of perihelion and aphelion for the next few years are:[6]
| Year | Perihelion | Aphelion | ||
|---|---|---|---|---|
| Date | Hour[A] (UT) | Date | Hour[A] (UT) | |
| 2007 | January 3 | 20:00 | July 7 | 00:00 |
| 2008 | January 3 | 00:00 | July 4 | 08:00 |
| 2009 | January 4 | 15:00 | July 4 | 02:00 |
| 2010 | January 3 | 00:00 | July 6 | 12:00 |
| 2011 | January 3 | 19:00 | July 4 | 15:00 |
| 2012 | January 5 | 01:00 | July 5 | 04:00 |
| 2013 | January 2 | 05:00 | July 5 | 15:00 |
| 2014 | January 4 | 12:00 | July 4 | 00:00 |
| 2015 | January 4 | 07:00 | July 6 | 20:00 |
| 2016 | January 2 | 23:00 | July 4 | 16:00 |
| 2017 | January 4 | 14:00 | July 3 | 20:00 |
| 2018 | January 3 | 06:00 | July 6 | 17:00 |
| 2019 | January 3 | 05:00 | July 4 | 22:00 |
| 2020 | January 5 | 08:00 | July 4 | 12:00 |
Planetary perihelion and aphelion
The images below show the perihelion and aphelion points of the inner and outer planets respectively.
 The perihelion and aphelion points of the inner planets of the Solar System |
 The perihelion and aphelion points of the outer planets of the Solar System |
See also
- Eccentric anomaly
- Elliptic orbit
Notes and references
- ^ The source data is specific only to the hour; the table value minutes are placeholders only.
- ↑ "Apollo 15 Mission Report". Glossary. http://history.nasa.gov/alsj/a15/a15mr-f.htm. Retrieved October 16 2009.
- ↑ R. Schodel, T. Ott, R. Genzel, R. Hofmann, M. Lehnert, A. Eckart, N. Mouawad, T. Alexander, M.J. Reid, R. Lenzen, M. Hartung, F. Lacombe, D. Rouan, E. Gendron, G. Rousset, A.-M. Lagrange, W. Brandner, N. Ageorges, C. Lidman, A.F.M. Moorwood, J. Spyromilio, N. Hubin, and K.M. Menten, "Closest Star Seen Orbiting the Supermassive Black Hole at the Centre of the Milky Way," Nature 419, 694-696 (17 October 2002), doi:10.1038/nature01121.
- ↑ Properly pronounced 'affelion' because the (neo) Greek is αφήλιον, although the hypercorrection 'ap-helion' is commonly heard.
- ↑ "Apsis". Glossary of Terms. National Solar Observatory. 2005-02-21. http://www.nso.edu/press/glossary.html#apsis. Retrieved 2006-09-30.
- ↑ NASA.gov
- ↑ Earth's Seasons: Equinoxes, Solstices, Perihelion, and Aphelion - 2000-2020 —U.S. Naval Observatory, Astronomical Applications Department (accessed 2010-07-06).
External links
- Apogee - Perigee Photographic Size Comparison, perseus.gr
- Aphelion - Perihelion Photographic Size Comparison, perseus.gr
- Aphelion - Perihelion Dates and Times, islandnet.com
|
||||||||||||||||||||||||||||||||||||||||||||||

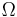



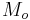
 True anomaly
True anomaly Semi-minor axis
Semi-minor axis
 Eccentric anomaly
Eccentric anomaly Mean longitude
Mean longitude True longitude
True longitude