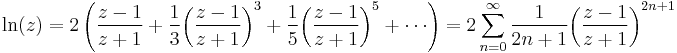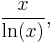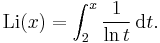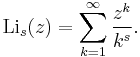Logarithm


In mathematics, the logarithm of a number to a given base is the power or exponent to which the base must be raised in order to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 3 is the power to which ten must be raised to produce 1000: 103 = 1000, so log101000 = 3. Only positive real numbers have real number logarithms; negative and complex numbers have complex logarithms.
The logarithm of x to the base b is written logb(x) or, if the base is implicit, as log(x). So, for a number x, a base b and an exponent y,
The bases used most often are 10 for the common logarithm, e for the natural logarithm, and 2 for the binary logarithm.
An important feature of logarithms is that they reduce multiplication to addition, by the formula:
That is, the logarithm of the product of two numbers is the sum of the logarithms of those numbers.
Similarly, logarithms reduce division to subtraction by the formula:
That is, the logarithm of the quotient of two numbers is the difference between the logarithms of those numbers.
The use of logarithms to facilitate complicated calculations was a significant motivation in their original development. Logarithms have applications in fields as diverse as statistics, chemistry, physics, astronomy, computer science, economics, music, and engineering.
Contents |
Logarithm of positive real numbers
Definition
The logarithm of a number y with respect to a number b is the power to which b has to be raised in order to give y. In symbols, the logarithm is the number x satisfying the following equation:
- bx = y.
The logarithm x is denoted logb(y). (Some European countries write blog(y) instead.[1]) The number b is called base. For b = 2, for example, this means
- log2(8) = 3,
since 23 = 2 · 2 · 2 = 8. Another example is
since
For the logarithm to exist, one has to require the base b to be a positive real number unequal to 1. Secondly, y has to be a positive real number. These restrictions are necessary because of the following: the logarithm has been defined to be the solution of an equation. For this to be meaningful, it is thus necessary to ensure that there is one solution. Secondly, to avoid ambiguity, it is necessary to ensure that there is only one solution. Both points are satisfied with the said restrictions on b and y, but are not without these restrictions. This is explained below.

The right image shows how to determine (approximately) the logarithm. Given the graph (in red) of the function f(x) = 2x, the logarithm log2(y) is the For any given number y (y = 3 in the image), the logarithm of y to the base 2 is the x-coordinate of the intersection point of the graph and the horizontal line intersecting the vertical axis at 3.
Logarithmic identities
There are three important formulas, sometimes called logarithmic identities, relating various logarithms to one another. The first is about the logarithm of a product, the second about logarithms of powers and the third involves logarithms with respect to different bases.
Logarithm of a product
The logarithm of a product is the sum of the two logarithms. That is, for any two positive real numbers x and y, and a given positive base b, the following identity holds:
- logb(x · y) = logb(x) + logb(y).
For example,
- log3(9 · 27) = log3(243) = 5,
since 35 = 243. On the other hand, the sum of log3(9) = 2 and log3(27) = 3 also equals 5. In general, that identity is derived from the relation of powers and multiplication:
- bs · bt = bs + t.
Indeed, with the particular values s = logb(x) and t = logb(y), the preceding equality implies
- logb(bs · bt) = logb(bs + t) = s + t = logb(bs) + logb(bt).
By virtue of this identity, logarithms make lengthy numerical operations easier to perform by converting multiplications to additions. The manual computation process is made easy by using tables of logarithms, or a slide rule. The property of common logarithms pertinent to the use of log tables is that any decimal sequence of the same digits, but different decimal-point positions, will have identical mantissas and differ only in their characteristics.
Logarithm of a power
The logarithm of the p-th power of a number x is p times the logarithm of that number. In symbols:
- logb(xp) = p logb(x).
As an example,
- log2(64) = log2(43) = 3 · log2(4) = 3 · 2 = 6.
This formula can be proven as follows: the logarithm of x is the number to which the base b has to be raised in order to yield x. In other words, the following identity holds:
- x = blogb(x).
Raising both sides of the equation to the p-th power (exponentiation) shows
- xp = (blogb(x))p = bp · logb(x).
(At this point, the identity (de)f = de · f was used, where d, e and f are positive real numbers.) Thus, the logb of the left hand side, logb(xp), and of the right hand side, p · logb(x), agree. The sought formula is proven.
Besides reducing multiplication operations to addition, and exponentiation to multiplication, logarithms reduce division to subtraction, and roots to division. For example,
Change of base
The third important rule for calculating logarithms is the following formula calculating the logarithm of a fixed number x to one base in terms of the one to another base:
This is shown as follows: the left hand side of the above is the unique number a such that ba = x. Therefore
- logk(x) = logk(ba) = a · logk(b).
The general restriction b ≠ 1 implies logkb ≠ 0, since b0 = 1. Thus, dividing the preceding equation by logkb shows the above formula.
As a practical consequence, logarithms with respect to any base k can be calculated, e.g. using a calculator, if logarithms to the base b are available. From a more theoretical viewpoint, this result implies that the graphs of all logarithm functions (whatever the base b) are similar to each other.
One way of viewing the change-of-base formula is to say that in the expression
the two bs "cancel", leaving logk x.
Particular bases
While the definition of logarithm applies to any positive real number b (1 is excluded, though), a few particular choices for b are more commonly used. These are b = 10, b = e (the mathematical constant ≈ 2.71828…), and b = 2. The different standards come about because of the different properties preferred in different fields. For example, it has been argued that common logarithms are easier to deal with than other ones, since in the decimal number system the powers of 10 have a simple representation.[2] Mathematical analysis, on the other hand, prefers the base b = e because of the "natural" properties explained below.
The following table lists common notations for logarithms to these bases and the fields where they are used. Instead of writing logb(x), it is common in many disciplines to omit the base, log(x), when intended base can be determined from context. The notations suggested by the International Organization for Standardization (ISO 31-11) are underlined in the table below.[3] Given a number n and its logarithm logb(n), the base b can be determined by the following formula:
This follows from the change-of-base formula above.
| Base b | Name | Notations for logb(x) | Used in |
|---|---|---|---|
| 2 | binary logarithm | lb(x)[4], ld(x), log(x) (in computer science, on calculators), lg(x)[5] | computer science, information theory |
| e | natural logarithm | ln(x)a[›], log(x) (in mathematics and many programming languages,[6] | mathematical analysis, statistics, economics and some engineering fields |
| 10 | common logarithm | lg(x)[7], log(x) (in engineering, biology, astronomy), | various engineering fields, especially for power levels and power ratios (see decibel and see below); logarithm tables |
Analytic properties
Domain of definition
In the above definition, it was required that b be positive, but unequal to 1, and that y be positive. If these assumptions are met, the equation
- bx = y
has exactly one solution x. To prove this, it is helpful to consider the cases b > 1 and 0 < b < 1 separately. If b > 1, bx is a continuous, strictly monotonic function from the reals to the positive reals, so it has an inverse function from the positive reals to the reals, which is denoted by logb (x). If 0 < b < 1, then the identity
can be used to define
Logarithm as a function

In the more highbrow language of calculus, the above proof amounts to saying that the function f(x) = bx is strictly increasing, takes arbitrarily big and small positive values and is continuous (intuitively, the function does not "jump": the graph can be drawn without lifting the pen). These properties, together with the intermediate value theorem of elementary calculus ensure that there is indeed exactly one solution x to the equation
- f(x) = bx = y,
for any given positive y.
The expression logb(x) depends on both b and x, but the term logarithm function (or logarithmic function) refers to a function of the form logb(x) in which the base b is fixed and x is variable, thus yielding a function that assigns to any x its logarithm logb(x). The word "logarithm" is often used to refer to a logarithm function itself as well as to particular values of this function. The above definition of logarithms were done indirectly by means of the exponential function. A compact way of rephrasing that definition is to say that the base-b logarithm function is the inverse function of the exponential function bx: a point (t, u = b(t)) on the graph of the exponential function yields a point (u, t = logbu) on the graph of the logarithm and vice versa. Geometrically, this corresponds to the statement that the points correspond one to another upon reflecting them at the diagonal line x = y.
Using this relation to the exponential function, calculus tells that the logarithm function is continuous (it does not "jump", i.e., the logarithm of x changes only little when x varies only little). What is more, it is differentiable (intuitively, this means that the graph of logb(x) has no sharp "corners").
Integral representation of the natural logarithm

When b = e (Euler's number), the natural logarithm ln(t) = loge(t) can be shown to satisfy the following identity:
In prose, the natural logarithm of t agrees with the integral of 1/x dx from 1 to t, that is to say, the area between the x-axis and the function 1/x, ranging from x = 1 to x = t. This is depicted at the right. Some authors use the right hand side of this equation as a definition of the natural logarithm.[8] The formulae of logarithms of products and powers mentioned above can be derived directly from this presentation of the natural logarithm. The product formula ln(tu) = ln(t) + ln(u) is deduced in the following way:
The "=" labelled (1) used a splitting of the integral into two parts, the equality (2) is a change of variable (w = x/t). This can also be understood geometrically. The integral is split into two parts (shown in yellow and blue). The key point is this: rescaling the left hand blue area in vertical direction by the factor t and shrinking it by the same factor in the horizontal direction does not change its size. Moving it appropriately, the area fits the graph of the function 1/x again. Therefore, the left hand area, which is the integral of f(x) from t to tu is the same as the integral from 1 to u:

The power formula ln(tr) = r ln(t) is derived similarly:
The second equality is using a change of variables, w := x1/r, while the third equality follows from integration by substitution.
Not only the integral over 1/x is tied to the logarithm, the harmonic series,
also is: as n tends to infinity, the series
converges to a number known as Euler–Mascheroni constant. Little is known about it—not even whether it is a rational number or not.[9]
Derivative and antiderivative
The derivative of the natural logarithm is given by
This can be derived either from the definition as the inverse function of exp(x), using the chain rule,[10] or from the above integral formula, using the fundamental theorem of calculus. More generally the derivative with a generalised functional argument f(x) is
For this reason the quotient at right hand side is called logarithmic derivative of f. The antiderivative of the natural logarithm ln(x) is
Derivatives and antiderivatives of logarithms to other bases can be derived therefrom using the formula for change of bases.
Calculation
Taylor series
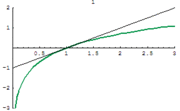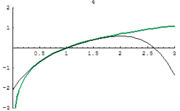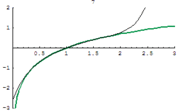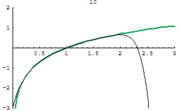
There are several series for calculating natural logarithms.[11] For all complex numbers z satisfying |1 − z| < 1, a simple, though inefficient, series is
Actually, this is the Taylor series expansion of the natural logarithm at z = 1. It is derived from the geometric series (which is the Taylor series of 1/(1 − x)), which converges for |x| < 1:
Taking the indefinite integral of both sides yields
and the above expression is obtained by substituting x by 1 − z (so that 1 − x = z).
More efficient series
Another series is
for complex numbers z with positive real part. This series can be derived from the above Taylor series. The series converges most quickly if z is close to 1. For example, for z = 1.5, the first three terms of this series approximate ln(1.5) with an error of about 3·10−6. (For comparison, the above Taylor series needs 13 terms to achieve that precision.) The quick convergence for z close to 1 can be taken advantage of in the following way: given a low-accuracy approximation y ≈ ln(z) and putting A = z/exp(y), the logarithm of z is
- ln(z) = y + ln(A).
The better the initial approximation y is, the closer A is to 1, so its logarithm can be calculated efficiently. The calculation of A can be done using the exponential series, which converges quickly provided y is not too large. Calculating the logarithm of larger z can be reduced to smaller values of z by writing z = a · 10b, so that ln(z) = ln(a) + b · ln(10).
Computation using significands
In most computers, real numbers are modelled by floating points, which are usually stored as
- x = m · 2n.
In this representation m is called significand and n is the exponent. Therefore
- logb(x) = logb(m) + n logb(2),
so that in order to compute the logarithm of x, it suffices to calculate logb(m) for some m such that 1 ≤ m < 2. Having m in this range means that the value u = (m − 1)/(m + 1) is always in the range 0 ≤ u < 1/3. Some machines use the significand in the range 0.5 ≤ m < 1 and in that case the value for u will be in the range −1/3 < u ≤ 0. In either case, the series is even easier to compute.
The binary (base b = 2) logarithm of a number x can be approximated using the binary logarithm algorithm.
Logarithm of a negative or complex number
The above definition of logarithms of positive real numbers can be extended to complex numbers. This generalization known as complex logarithm requires more care than the logarithm of positive real numbers. Any complex number z can be represented as z = x + iy, where x and y are real numbers and i is the imaginary unit. The intent of the logarithm is—as with the natural logarithm of real numbers above— to find a complex number a such that the exponential of a equals z:
- ea = z.
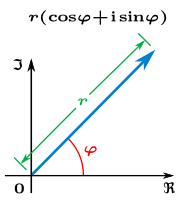
This can be solved for any z ≠ 0, however there are multiple solutions. To see this, it is convenient to use the polar form of z, i.e., to express z as
- z = r(cos(φ) + i sin(φ))
where 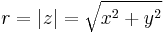 is the absolute value of z and φ = arg(z) an argument of z, that is, is any angle such that x = r cos(φ) and y = r sin(φ).[12] Geometrically, the absolute value is the distance of z to the origin and the argument is the angle between the x-axis and the line passing through the origin and z. The argument φ is not unique: φ' = φ + 2π is an argument, too, since "winding" around the circle counter-clock-wise once corresponds to adding 2π (360 degrees) to φ. However, there is exactly one argument φ such that −π < φ and φ ≤ π, called the principal argument and denoted Arg(z), with a capital A.[13] (The normalization 0 ≤ φ < 2π for the principal argument also appears in the literature.[14])
is the absolute value of z and φ = arg(z) an argument of z, that is, is any angle such that x = r cos(φ) and y = r sin(φ).[12] Geometrically, the absolute value is the distance of z to the origin and the argument is the angle between the x-axis and the line passing through the origin and z. The argument φ is not unique: φ' = φ + 2π is an argument, too, since "winding" around the circle counter-clock-wise once corresponds to adding 2π (360 degrees) to φ. However, there is exactly one argument φ such that −π < φ and φ ≤ π, called the principal argument and denoted Arg(z), with a capital A.[13] (The normalization 0 ≤ φ < 2π for the principal argument also appears in the literature.[14])
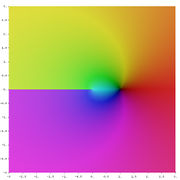
It is a fact proven in complex analysis that z = reiφ. Consequently,
- a = ln(r) + i φ
is such that the a-th power of e equals z, so that a qualifies being called logarithm of z. When φ is chosen to be the principal argument, a is called principal value of the logarithm, denoted Log(z). The principal argument of any positive real number is 0; hence the principal logarithm of such a number is always real and equals the natural logarithm. The graph at the right depicts Log(z). The discontinuity, i.e., jump in the hue at the negative part of the x-axis is due to jump of the principal argument at this locus. This behavior can only be circumvented by dropping the range restriction on φ. Then, however, both the argument of z and, consequently, its logarithm become multi-valued functions. In fact, any logarithm of z can be shown to be of the form
- ln(r) + i (φ + 2nπ),
where φ is the principal argument Arg(z). Analogous formula for principal values of logarithm of products and powers for complex numbers do in general not hold.
For any complex number b ≠ 0 and 1, the complex logarithm logb(z) with base b is defined as ln(z)/ln(b), the principal value of which is given by the principal values of ln(z) and ln(b).
Uses and occurrences

Logarithms appear in many places, within and outside mathematics. The logarithmic spiral, for example, appears (approximately) in various guises in nature, such as the shells of nautilus.[15] Logarithms also appear in formulas in various sciences, such as the Tsiolkovsky rocket equation or Fenske equation.
The logarithm of a positive integer x to a given base shows how many digits are needed to write that integer in that base. For instance, the common logarithm log10(x) is linked to the number n of numerical digits of x: n is the smallest integer strictly bigger than log10(x), i.e., the one satisfying the inequalities:
- n − 1 ≤ log10(x) < n.
Similarly, the number of binary digits (or bits) needed to store a positive integer x is the smallest integer strictly bigger than log2(x).
Calculation of products, powers and roots
Logarithms can be used to reduce multiplications and exponentiations to additions, thus making feasible many calculations that are otherwise too laborious. This fact was the historical motivation for logarithms. The use of logarithms was an essential skill until computers and calculators became available.
The product of two numbers c and d can be calculated by the following formula:
- c · d = blogbc · blogbd = b(logbc + logbd).
Using a table of logarithms, logbc and logbd can be looked up. After calculating their sum, an easy operation, the antilogarithm of that sum is looked up in a table, which is the desired product. For manual calculations that demand any appreciable precision, this process, requiring three lookups and a sum, is much faster than performing the multiplication. To achieve seven decimal places of accuracy requires a table that fills a single large volume; a table for nine-decimal accuracy occupies a few shelves. The precision of the approximation can be increased by interpolating between table entries.
Divisions can be performed similarly: 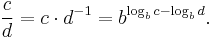 Moreover,
Moreover,
- cd = b(logbc) · d
reduces the exponentiation to looking up the logarithm of c, multiplying it with d (possibly using the previous method) and looking up the antilogarithm of the product. Roots ![\sqrt[d]{c}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/fda5de982813c3145765261ac115125e.png) can be calculated this way, too, since
can be calculated this way, too, since ![\sqrt[d]{c} = c^{\frac 1 d}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/307d8e195ac1a29325fdc8d0268f4c1e.png) .
.
One key application of these techniques was celestial navigation. Once the invention of the chronometer made possible the accurate measurement of longitude at sea, mariners had everything necessary to reduce their navigational computations to mere additions. A five-digit table of logarithms and a table of the logarithms of trigonometric functions sufficed for most purposes, and those tables could fit in a small book. Another critical application with even broader impact was the slide rule, until the 1970s an essential calculating tool for engineers and scientists. The slide rule allows much faster computation than techniques based on tables, but provides much less precision (although slide rule operations can be chained to calculate answers to any arbitrary precision).

Logarithmic scale

Various quantities in science are expressed as logarithms of other quantities, a concept known as logarithmic scale. For example, the Richter scale measures the strength of an earthquake by taking the common logarithm of the energy emitted at the earthquake. Thus, an increase in energy by a factor of 10 adds one to the Richter magnitude; a 100-fold energy results in +2 in the magnitude etc.[16] Considering the logarithm instead of the value, here the energy of the quake, reduces the range of possible values to a much smaller range. A second example is the pH in chemistry: it is the negative of the base-10 logarithm of the activity of hydronium ions (H3O+, the form H+ takes in water).[17] The activity of hydronium ions in neutral water is 10−7 mol/L at 25 °C, hence a pH of 7. Vinegar, on the other hand, has a pH of about 3. The difference of 4 corresponds to a ratio of 104 of the activity, that is, vinegar's hydronium ion activity is about 10−3 mol/L. In a similar vein, the decibel (symbol dB) is a unit of measure which is the base-10 logarithm of ratios. For example it is used to quantify the loss of voltage levels in transmitting electrical signals[18] or to describe power levels of sounds in acoustics.[19] In spectrometry and optics, the absorbance unit used to measure optical density is equivalent to −10 dB. The apparent magnitude measures the brightness of stars logarithmically.
Semilog graphs or log-linear graphs use this concept for visualization: one axis, typically the vertical one, is scaled logarithmically. This way, exponential functions of the form f(x) = a · bx appear as a straight line whose slope is proportional to b. In a similar vein, log-log graphs scale both axes logarithmically.[20]
Psychology
In psychophysics, the Weber–Fechner law proposes a logarithmic relationship between stimulus and sensation (though Stevens' power law is typically more accurate). The logarithm appears in situations when the smallest change ΔS of some stimulus S that an observer can still notice is proportional to S, by the above relation of the natural logarithm and the integral over dS / S. (Similar formulas also appear in other sciences, such as the Clausius–Clapeyron relation.) Hick's law proposes a logarithmic relation between the time individuals take for choosing an alternative and the number of choices they have.[21]
Mathematically untrained individuals tend to estimate numerals with a logarithmic spacing, i.e., the position of a presented numeral correlates with the logarithm of the given number so that smaller numbers are given more space than bigger ones. With increasing mathematical training this logarithmic representation becomes more and more linear, as confirmed both in Western school children, comparing second to sixth graders,[22] as well as in comparison between American and indigene cultures.[23]
Complexity and entropy
A function f(x) is said to grow logarithmically, if it is (sometimes approximately) proportional to the logarithm. (Biology, in describing growth of organisms, uses this term for an exponential function, though.[24]) It is irrelevant to which base the logarithm is taken, since choosing a different base amounts to multiplying the result by a constant, as follows from the formula above. For example, any natural number N can be represented in binary form in no more than (log2(N)) + 1 bits. I.e., the amount of hard disk space on a computer grows logarithmically as a function of the size of the number to store. Corresponding calculations carried out using loge will lead to results in nats which may lack this intuitive interpretation. However, the change amounts to a factor of loge2≈0.69—twice as many values can be encoded with one additional bit, which corresponds to an increase of about 0.69 nats. A similar example is the relation of decibel (dB), using a common logarithm (b = 10) vis-à-vis neper, based on a natural logarithm.
Some disciplines disregard the factor resulting from choosing different bases of logarithms. For example, complexity theory, a branch of computer science, describes the asymptotic behavior of algorithms by making statements like "the behavior of the algorithm is logarithmic". For example, sorting N items using the quicksort algorithm typically requires time proportional to the product N · log(N). Using big O notation, the complexity is denoted as
- O(N · log(N)),
which is a lot slower a growth than, say the complexity O(N2) of bubble sort.
Using logarithms, the notion of entropy in information theory is a measure of quantity of information. If a message recipient may expect any one of N possible messages with equal likelihood, then the amount of information conveyed by any one such message is quantified as log2 N bits.[25] In the same vein, the concept of entropy also appears in thermodynamics. Fractal dimension and Hausdorff dimension measure how much space geometric structures occupy.
| Example | point | (straight) line | Koch curve | Sierpinski triangle | plane | Apollonian sphere |
 |
 |
|||||
| Hausdorff dimension | 0 | 1 | log(4)/log(3) ≈ 1.262 | log(3)/log(2) ≈ 1.585 | 2 | ≈ 2.474 |
Pure mathematics

Natural logarithms have a tendency to appear in number theory. For any given number x, the number of prime numbers less than or equal to x is denoted π(x). In its simplest form, the prime number theorem asserts that π(x) is approximately given by
in the sense that the ratio of π(x) and that fraction approaches 1 when x tends to infinity.[26] This can be rephrased by saying that the probability that a randomly chosen number between 1 and x is prime is indirectly proportional to the numbers of decimal digits of x. A far better estimate of π(x) is given by the offset logarithmic integral function Li(x), defined by
The Riemann hypothesis, one of the oldest open mathematical conjectures, can be stated in terms of comparing π(x) and Li(x).[27] The Erdős–Kac theorem describing the number of distinct prime factors also involves the natural logarithm.
By the formula calculating logarithms of products, the logarithm of n factorial, n! = 1 · 2 · ... · n, is given by
- ln(n!) = ln(1) + ln(2) + ... + ln(n).
This can be used to obtain Stirling's formula, an approximation for n! for large n.[28]
In geometry the logarithm is used to calculate the distance on the Poincaré half-plane model of the hyperbolic geometry.
Statistics

In inferential statistics, the logarithm of the data in a dataset can be used for parametric statistical testing if the original data do not meet the assumption of normality.
Logarithms appear in Benford's law, an empirical description of the occurrence of digits in certain real-life data sources, such as heights of buildings. The probability that the first decimal digit of the data in question is d (from 1 to 9) equals
- log10(d + 1) − log10(d),
irrespective of the unit of measurement.[29] Thus according to that law, about 30% of the data can be expected to have 1 as first digit, 18% start with 2 etc. Deviations from this pattern can be used to detect fraud in accounting.[30]
Music
Logarithms appear in the encoding of musical tones. In equal temperament, the frequency ratio depends only on the interval between two tones, not on the specific frequency, or pitch of the individual tones. Therefore, logarithms can be used to describe the intervals: the interval between two notes in semitones is the base-21/12 logarithm of the frequency ratio.[31] For finer encoding, as it is needed for non-equal temperaments, intervals are also expressed in cents, hundredths of an equally-tempered semitone. The interval between two notes in cents is the base-21/1200 logarithm of the frequency ratio (or 1200 times the base-2 logarithm). The table below lists some musical intervals together with the frequency ratios and their logarithms.
| Interval (two tones are played at the same time) | 1/72 tone play | Semitone play | Just major third play | Major third play | Tritone play | Octave play |
| Frequency ratio r | ![2^{\frac 1 {72}} = \sqrt[72] 2 \approx 1.0097](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/865744bf637a92d5be8a50ed6132367e.png) |
![2^{\frac 1 {12}} = \sqrt[12] 2 \approx 1.0595](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/e4b53f997f508f490aac0031448ecd54.png) |
 |
![2^{\frac 4 {12}} = \sqrt[12] {2^4} = \sqrt[3] 2 \approx 1.2599](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/59099a49cdd72627d30dd98eeaffa971.png) |
![2^{\frac 6 {12}} = \sqrt[12] {2^6} = \sqrt 2 \approx 1.4142](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/52201831b355bcd119957771f9df4095.png) |
2 |
![\log_{\sqrt[12] 2}(r) = 12 \cdot \log_2 (r)](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/6f6355d1c1d4c683ec374d920e27030c.png) , i.e., corresponding number of semitones , i.e., corresponding number of semitones |
1/6 | 1 | ≈ 3.86 | 4 | 6 | 12 |
![\log_{\sqrt[1200] 2}(r) = 1200 \cdot \log_2 (r)](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/83c46548d891f9fc19147daf9f9af238.png) , i.e., corresponding number of cents , i.e., corresponding number of cents |
16.67 | 100 | ≈ 386.31 | 400 | 600 | 1200 |
Related operations and generalizations
The cologarithm of a number is the logarithm of the reciprocal of the number: cologb(x) = logb(1/x) = −logb(x). This terminology is found primarily in older books.[32] The antilogarithm function antilogb(y) is the inverse function of the logarithm function logb(x); it can be written in closed form as by.[33] The antilog notation was common before the advent of modern calculators and computers: tables of antilogarithms to the base 10 were useful in carrying out computations by hand.[34] Today's applications of antilogarithms include certain electronic circuit components known as antilog amplifiers,[35] or the calculation of equilibrium constants of reactions involving electrode potentials.
The double or iterated logarithm, ln(ln(x)), is the inverse function of the double exponential function. The super- or hyper-4-logarithm is the inverse function of tetration. The super-logarithm of x grows even more slowly than the double logarithm for large x.
The Lambert W function is the inverse function of ƒ(w) = wew. Polylogarithm is a generalization of the logarithm defined by
For s = 1, it is related to the logarithm via Li1(z) = −ln(1 − z). For z = 1, on the other hand, Lis(1) yields the Riemann zeta function ζ(s).
From the pure mathematical perspective, the identity log(cd) = log(c) + log(d) expresses an isomorphism between the multiplicative group of the positive real numbers and the group of all the reals under addition. Logarithmic functions are the only continuous isomorphisms from the multiplicative group of positive real numbers to the additive group of real numbers.[36] By means of that isomorphism, the Lebesgue measure dx on R corresponds to the Haar measure dx/x on the positive reals.[37] In complex analysis and algebraic geometry, differential forms of the form (d log(f) =) df/f are known as forms with logarithmic poles.[38]
The discrete logarithm is a related notion in the theory of finite groups. It involves solving the equation bn = x, where b and x are elements of the group, and n is an integer specifying a power in the group operation. For some finite groups, it is believed that the discrete logarithm is very hard to calculate, whereas discrete exponentials are quite easy. This asymmetry has applications in public key cryptography.[39]
Logarithms can be defined for p-adic numbers,[40] quaternions and octonions. The logarithm of a matrix is the inverse of the matrix exponential.
History

The Indian mathematician Virasena worked with the concept of ardhaccheda: the number of times a number could be halved; effectively similar to the integer part of logarithms to base 2. He described various relations using this operation as well as working with logarithms in base 3 (trakacheda) and base 4 (caturthacheda).[41][42]
Michael Stifel published Arithmetica integra in Nuremberg in 1544; it contains a table of integers and powers of 2 that some have considered to be an early version of a logarithmic table.[43][44]
The method of logarithms was publicly propounded in 1614, in a book entitled Mirifici Logarithmorum Canonis Descriptio, by John Napier, Baron of Merchiston, in Scotland,[45] (Joost Bürgi independently discovered logarithms; however, he did not publish his discovery until four years after Napier). Early resistance to the use of logarithms was muted by Kepler's enthusiastic support and his publication of a clear and impeccable explanation of how they worked.[46]
Their use contributed to the advance of science, and especially of astronomy, by making some difficult calculations possible. Prior to the advent of calculators and computers, they were used constantly in surveying, navigation, and other branches of practical mathematics. It supplanted the more involved method of prosthaphaeresis, which relied on trigonometric identities as a quick method of computing products. Besides the utility of the logarithm concept in computation, the natural logarithm presented a solution to the problem of quadrature of a hyperbolic sector at the hand of Gregoire de Saint-Vincent in 1647.
At first, Napier called logarithms "artificial numbers" and antilogarithms "natural numbers". Later, Napier formed the word logarithm to mean a number that indicates a ratio: λόγος (logos) meaning proportion, and ἀριθμός (arithmos) meaning number. Napier chose that because the difference of two logarithms determines the ratio of the numbers they represent, so that an arithmetic series of logarithms corresponds to a geometric series of numbers. The term antilogarithm was introduced in the late 17th century and, while never used extensively in mathematics, persisted in collections of tables until they fell into disuse.
Napier did not use a base as we now understand it, but his logarithms were, up to a scaling factor, effectively to base 1/e. For interpolation purposes and ease of calculation, it is useful to make the ratio r in the geometric series close to 1. Napier chose r = 1 − 10−7 = 0.999999 (Bürgi chose r = 1 + 10−4 = 1.0001). Napier's original logarithms did not have log 1 = 0 but rather log 107 = 0. Thus if N is a number and L is its logarithm as calculated by Napier, N = 107(1 − 10−7) L. Since (1 − 10−7)107 is approximately 1/e, this makes L / 107 approximately equal to log1/e N/107.[4]

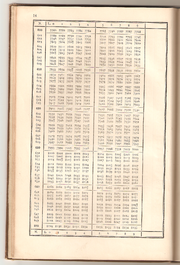
Tables of logarithms
Prior to the advent of computers and calculators, using logarithms for practical purposes was done with tables of logarithms, which contain both logarithms and antilogarithms with respect to some fixed base.
When the purpose was to facilitate arithmetic computations, base 10 was used, and logarithms of numbers between 1 and 10 by small increments (e.g. 0.01 or 0.001) appeared. There was no need for logarithms of other numbers (above 10 or below 1) because moving the decimal point corresponds to simply adding an integer to the logarithm. See Common logarithm for further details.
The following table lists the major tables of logarithms compiled in history:
| Year | Author | Range | Decimal places | Note |
|---|---|---|---|---|
| 1617 | Henry Briggs | 1–1000 | 8 | |
| 1624 | Henry Briggs Arithmetica Logarithmica | 1–20,000, 90,000–100,000 | 14 | |
| 1628 | Adriaan Vlacq | 20,000–90,000 | 10 | contained only 603 errors[47] |
| 1792–94 | Gaspard de Prony Tables du Cadastre | 1–100,000 and 100,000–200,000 | 19 and 24, respectively | "seventeen enormous folios",[48] never published |
| 1794 | Jurij Vega Thesaurus Logarithmorum Completus (Leipzig) | corrected edition of Vlacq's work | ||
| 1795 | François Callet (Paris) | 100,000–108,000 | 7 | |
| 1871 | Sang | 1–200,000 | 7 |
Briggs and Vlacq also published original tables of the logarithms of the trigonometric functions.
See also
- List of logarithm topics
- Logit
- Lyapunov exponents
- List of logarithmic identities
- Zech's logarithms
- Log-normal distribution
- Law of the iterated logarithm
- Logarithmic number system
- Logarithmic differentiation
- Logarithmic form, Log terminal, Log pair
- Log return
Notes
^ a: Some mathematicians disapprove of this notation. In his 1985 autobiography, Paul Halmos criticized what he considered the "childish ln notation," which he said no mathematician had ever used.[49] In fact, the notation was invented by a mathematician Irving Stringham.[50][51]
References
- Bateman, P. T.; Diamond, Harold G. (2004), Analytic number theory: an introductory course, World Scientific, ISBN 9789812560803, OCLC 492669517
- Shirali, Shailesh (2002), A Primer on Logarithms, Universities Press, ISBN 9788173714146
- ↑ ""Mathematisches Lexikon" at Mateh_online.at". http://www.mathe-online.at/mathint/lexikon/l.html.
- ↑ Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, ISBN 978-0-7641-1972-9, chapter 17, p. 275
- ↑ B. N. Taylor (1995). "Guide for the Use of the International System of Units (SI)". NIST Special Publication 811, 1995 Edition. US Department of Commerce. http://physics.nist.gov/Pubs/SP811/sec10.html#10.1.2.
- ↑ 4.0 4.1 Gullberg, Jan (1997). Mathematics: from the birth of numbers.. W. W. Norton & Co. ISBN 039304002X.
- ↑ This notation was suggested by Edward Reingold and popularized by Donald Knuth
- ↑ including C, C++, Java, Haskell, Fortran, Python, Ruby, and BASIC
- ↑ Weisstein, Eric W., "Common Logarithm" from MathWorld.
- ↑ Courant, Richard (1988), Differential and integral calculus. Vol. I, Wiley Classics Library, New York: John Wiley & Sons, MR1009558, ISBN 978-0-471-60842-4, see Section III.6
- ↑ Havil, Julian (2003), Gamma: Exploring Euler's Constant, Princeton University Press, ISBN 978-0-691-09983-5
- ↑ Lang, Serge (1997), Undergraduate analysis, Undergraduate Texts in Mathematics (2nd ed.), Berlin, New York: Springer-Verlag, MR1476913, ISBN 978-0-387-94841-6, section IV.2
- ↑ Handbook of Mathematical Functions, National Bureau of Standards (Applied Mathematics Series no. 55), June 1964, page 68.
- ↑ Moore, Theral Orvis; Hadlock, Edwin H. (1991), Complex analysis, World Scientific, ISBN 9789810202460, see Section 1.2
- ↑ Ganguly, S. (2005), Elements of Complex Analysis, Academic Publishers, ISBN 9788187504863, Definition 1.6.3
- ↑ Nevanlinna, Rolf Herman; Paatero, Veikko (2007), Introduction to complex analysis, AMS Bookstore, ISBN 978-0-8218-4399-4, section 5.9
- ↑ Maor, Eli (2009), E: The Story of a Number, Princeton University Press, ISBN 978-0-691-14134-3, see page 135
- ↑ Crauder, Bruce; Evans, Benny; Noell, Alan (2008), Functions and Change: A Modeling Approach to College Algebra (4th ed.), Cengage Learning, ISBN 978-0-547-15669-9, section 4.4.
- ↑ IUPAC (1997), A. D. McNaught, A. Wilkinson, ed., Compendium of Chemical Terminology ("Gold Book") (2nd ed.), Oxford: Blackwell Scientific Publications, doi:10.1351/goldbook, ISBN 0-9678550-9-8, http://goldbook.iupac.org/P04524.html
- ↑ Bakshi, U. A. (2009), Telecommunication Engineering, Technical Publications, ISBN 9788184317251, see Section 5.2
- ↑ Maling, George C. (2007), "Noise", in Rossing, Thomas D., Springer handbook of acoustics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-30446-5, section 23.0.2
- ↑ Bird, J. O. (2001), Newnes engineering mathematics pocket book (3rd ed.), Oxford: Newnes, ISBN 978-0-7506-4992-6, see section 34
- ↑ Welford, A. T. (1968), Fundamentals of skill, London: Methuen, ISBN 978-0-416-03000-6, OCLC 219156, p. 61
- ↑ Siegler, Robert S.; Opfer, John E. (2003). "The Development of Numerical Estimation. Evidence for Multiple Representations of Numerical Quantity". Psychological Science 14 (3): 237–43. doi:10.1111/1467-9280.02438
- ↑ Dehaene, Stanislas; Izard, Véronique; Spelke, Elizabeth; Pica, Pierre (2008). "Log or Linear? Distinct Intuitions of the Number Scale in Western and Amazonian Indigene Cultures". Science 320 (5880): 1217–1220. doi:10.1126/science.1156540. PMID 18511690
- ↑ Mohr, Hans; Schopfer, Peter (1995), Plant physiology, Berlin, New York: Springer-Verlag, ISBN 978-3-540-58016-4, see Chapter 19, p. 298
- ↑ Eco, Umberto (1989), The open work, Harvard University Press, ISBN 978-0-674-63976-8, see section III.I
- ↑ P. T. Bateman & Diamond 2004, Theorem 4.1
- ↑ P. T. Bateman & Diamond 2004, Theorem 8.15
- ↑ Slomson, Alan B. (1991), An introduction to combinatorics, London: CRC Press, ISBN 978-0-412-35370-3, see Chapter 4
- ↑ Tabachnikov, Serge (2005), Geometry and Billiards, Providence, R.I.: American Mathematical Society, pp. 36–40, ISBN 978-0-8218-3919-5, see Section 2.1
- ↑ Durtschi, Cindy; Hillison, William; Pacini, Carl (2004). "The Effective Use of Benford's Law in Detecting Fraud in Accounting Data". Journal of Forensic Accounting V: 17–34. http://www.auditnet.org/articles/JFA-V-1-17-34.pdf.
- ↑ Wright, David (2009), Mathematics and music, AMS Bookstore, ISBN 978-0-8218-4873-9, see Chapter 5
- ↑ Wooster Woodruff B, Smith David E: "Academic Algebra", page 360. Ginn & Company, 1902
- ↑ Abramowitz, Milton; Stegun, Irene A., eds. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover Publications, tenth printing, ISBN 978-0-486-61272-0, see section 4.7., p. 89
- ↑ Silas Whitcomb Holman (1918). Computation Rules and Logarithms. Macmillan and Co.. http://books.google.com/?id=Hkc4AAAAMAAJ&pg=PR30&dq=antilog+tables.
- ↑ Forrest M. Mims (2000). The Forrest Mims Circuit Scrapbook. Newnes. ISBN 1878707485. http://books.google.com/?id=STzitya5iwgC&pg=PA7&dq=antilog-amplifier.
- ↑ Bourbaki, Nicolas (1998), General topology. Chapters 5--10, Elements of Mathematics, Berlin, New York: Springer-Verlag, MR1726872, ISBN 978-3-540-64563-4, see section V.4.1
- ↑ Ambartzumian, R. V. (1990), Factorization calculus and geometric probability, Cambridge University Press, ISBN 978-0-521-34535-4, see Section 1.4
- ↑ Esnault, Hélène; Viehweg, Eckart (1992), Lectures on vanishing theorems, DMV Seminar, 20, Birkhäuser Verlag, MR1193913, ISBN 978-3-7643-2822-1, see section 2
- ↑ Stinson, Douglas Robert (2006), Cryptography: Theory and Practice (3rd ed.), London: CRC Press, ISBN 978-1-58488-508-5
- ↑ Katok, Svetlana (2007), p-adic analysis compared with real, Student mathematical library, 37, AMS Bookstore, ISBN 978-0-8218-4220-1, Section 3.4.1.
- ↑ Gupta, R. C. (2000), "History of Mathematics in India", Students' Britannica India: Select essays, Popular Prakashan, p. 329, http://books.google.co.uk/books?id=-xzljvnQ1vAC&pg=PA329&lpg=PA329&dq=Virasena+logarithm&source=bl&ots=BeVpLXxdRS&sig=_h6VUF3QzNxCocVgpilvefyvxlo&hl=en&ei=W0xUTLyPD4n-4AatvaGnBQ&sa=X&oi=book_result&ct=result&resnum=2&ved=0CBgQ6AEwATgK#v=onepage&q=Virasena%20logarithm&f=false
- ↑ Singh, A. N., Lucknow University, http://www.jainworld.com/JWHindi/Books/shatkhandagama-4/02.htm
- ↑ Walter William Rouse Ball (1908). A short account of the history of mathematics. Macmillan and Co. p. 216. http://books.google.com/books?id=egY6AAAAMAAJ&pg=PA216&dq=%22arithmetica+integra%22+logarithms&hl=en&ei=iG9jTIvnN4P78Aagv8nICg&sa=X&oi=book_result&ct=result&resnum=1&ved=0CCUQ6AEwAA#v=onepage&q=%22arithmetica%20integra%22%20logarithms&f=false.
- ↑ Vivian Shaw Groza and Susanne M. Shelley (1972). Precalculus mathematics. 9780030776700. p. 182. ISBN 9780030776700. http://books.google.com/books?id=yM_lSq1eJv8C&pg=PA182&dq=%22arithmetica+integra%22+logarithm&hl=en&ei=ijhjTPqEJIL58Aal6MTTCg&sa=X&oi=book_result&ct=result&resnum=7&ved=0CFIQ6AEwBg#v=onepage&q=stifel&f=false.
- ↑ Ernest William Hobson. John Napier and the invention of logarithms. 1614. The University Press, 1914.
- ↑ (section "Astronomical Tables")
- ↑ "this cannot be regarded as a great number, when it is considered that the table was the result of an original calculation, and that more than 2,100,000 printed figures are liable to error.", Athenaeum, 15 June 1872. See also the Monthly Notices of the Royal Astronomical Society for May 1872.
- ↑ English Cyclopaedia, Biography, Vol. IV., article "Prony."
- ↑ Paul Halmos (1985). I Want to Be a Mathematician: An Automathography. Springer-Verlag. ISBN 978-0387960784.
- ↑ Irving Stringham (1893). Uniplanar algebra: being part I of a propædeutic to the higher mathematical analysis. The Berkeley Press. p. xiii. http://books.google.com/?id=hPEKAQAAIAAJ&pg=PR13&dq=%22Irving+Stringham%22+In-natural-logarithm&q=.
- ↑ Roy S. Freedman (2006). Introduction to Financial Technology. Academic Press. p. 59. ISBN 9780123704788. http://books.google.com/?id=APJ7QeR_XPkC&pg=PA59&dq=%22Irving+Stringham%22+logarithm+ln&q=%22Irving%20Stringham%22%20logarithm%20ln.
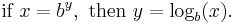
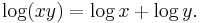
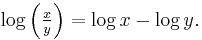
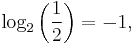
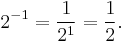
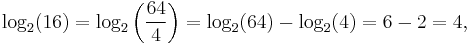
![\log_2(\sqrt[3]4) = \frac {1}{3} \log_2 (4) = \frac {2}{3}. \,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/bdb9af437ed3f9521db7e3647904748c.png)
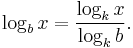
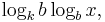
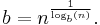
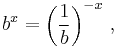
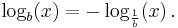
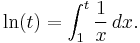
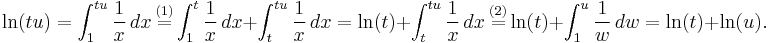
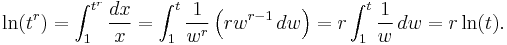
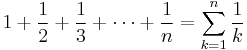
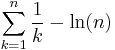
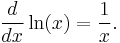
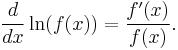
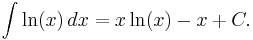
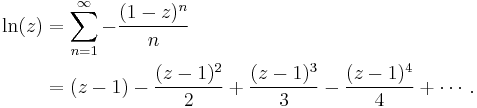
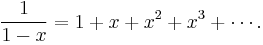
![\begin{align}
-\ln(1-x) & = x + \frac{x^2}{2} + \frac{x^3}{3} + \frac{x^4}{4} + \cdots \\[6pt]
\ln(1-x) & = -x - \frac{x^2}{2} - \frac{x^3}{3} - \frac{x^4}{4} - \cdots.
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/e579a753bc1e9194a58232cac04c12b3.png)