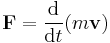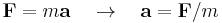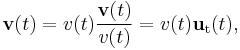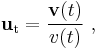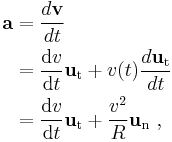Acceleration
| Classical mechanics | ||||||||||
History of classical mechanics · Timeline of classical mechanics
|
||||||||||
In physics, acceleration is the rate of change of velocity over time.[1] In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity.[2][3] Acceleration has the dimensions L T −2. In SI units, acceleration is measured in meters per second squared (m/s2).
In common speech, the term acceleration commonly is used for an increase in speed (the magnitude of velocity); a decrease in speed is called deceleration. In physics, a change in the direction of velocity also is an acceleration: for rotary motion, the change in direction of velocity results in centripetal (toward the center) acceleration; where as the rate of change of speed is a tangential acceleration.
In classical mechanics, for a body with constant mass, the acceleration of the body is proportional to the net force acting on it (Newton's second law):
where F is the resultant force acting on the body, m is the mass of the body, and a is its acceleration.
Contents |
Average and instantaneous acceleration
Average acceleration is the change in velocity (Δv) divided by the change in time (Δt). Instantaneous acceleration is the acceleration at a specific point in time which is for a very short interval of time as Δt approaches zero.
Tangential and centripetal acceleration
The velocity of a particle moving on a curved path as a function of time can be written as:
with v(t) equal to the speed of travel along the path, and
a unit vector tangent to the path pointing in the direction of motion at the chosen moment in time. Taking into account both the changing speed v(t) and the changing direction of ut, the acceleration of a particle moving on a curved path on a planar surface can be written using the chain rule of differentiation as:
where un is the unit (inward) normal vector to the particle's trajectory, and R is its instantaneous radius of curvature based upon the osculating circle at time t. These components are called the tangential acceleration and the radial acceleration or centripetal acceleration (see also circular motion and centripetal force).
Extension of this approach to three-dimensional space curves that cannot be contained on a planar surface leads to the Frenet-Serret formulas.[4][5]
Relation to relativity
After completing his theory of special relativity, Albert Einstein realized that forces felt by objects undergoing constant proper acceleration are actually feeling themselves being accelerated, so that, for example, a car's acceleration forwards would result in the driver feeling a slight pressure between himself and his seat. In the case of gravity, which Einstein concluded is not actually a force, this is not the case; acceleration due to gravity is not felt by an object in free-fall. This was the basis for his development of general relativity, a relativistic theory of gravity.
Notes
- ↑ Crew, Henry (2008). The Principles of Mechanics. BiblioBazaar, LLC. pp. 43. ISBN 0559368712.
- ↑ Bondi, Hermann (1980). Relativity and Common Sense. Courier Dover Publications. pp. 3. ISBN 0486240215.
- ↑ Lehrman, Robert L. (1998). Physics the Easy Way. Barron's Educational Series. pp. 27. ISBN 0764102362.
- ↑ Larry C. Andrews & Ronald L. Phillips (2003). Mathematical Techniques for Engineers and Scientists. SPIE Press. p. 164. ISBN 0819445061. http://books.google.com/books?id=MwrDfvrQyWYC&pg=PA164&dq=particle+%22planar+motion%22&lr=&as_brr=0&sig=ACfU3U2LpH6ofhuuC2UiED0pf38wbspY8A#PPA164,M1.
- ↑ Ch V Ramana Murthy & NC Srinivas (2001). Applied Mathematics. New Delhi: S. Chand & Co.. p. 337. ISBN 81-219-2082-5. http://books.google.com/books?id=Q0Pvv4vWOlQC&pg=PA337&vq=frenet&dq=isbn=8121920825&source=gbs_search_s&sig=ACfU3U3S5vGMS-NnraAEmpBf6B9bB2wK6A.
See also
- Uniform acceleration
- Angular acceleration
- Gravitational acceleration
- Coordinate vs. physical acceleration
- Kinematics/derivatives of position
- Equations of motion
- Proper acceleration
- 0 to 60 mph
- Shock (mechanics)
- Specific force
External links
- Acceleration and Free Fall - a chapter from an online textbook
- Science aid: Movement
- Science.dirbix: Acceleration
- Acceleration Calculator
- Motion Characteristics for Circular Motion
- Practical Guide to Accelerometers
- Acceleration Converter Converts common acceleration units.
- Acceleration Calculator Simple acceleration unit converter
|
|||||||