String theory

String theory
Calabi-Yau.png
Superstring theory
Theory
String theory
Superstrings
Bosonic string theory
M-theory (simplified)

Type I string · Type II string
Heterotic string
String field theory
Holographic principle

String theory is a still-developing approach to theoretical physics, whose original building blocks are one-dimensional extended objects called strings. String theory attempts to reconcile quantum mechanics with general relativity in order to describe a quantum theory of gravity.

Since its birth as the dual resonance model which described the strongly interacting hadrons as strings, the term string theory has changed to include any of a group of related superstring theories which unite them. One shared property of all these theories is the holographic principle. String theory itself consists of many theories with different mathematical formulas. The logical coherence of the approach, however, and the fact that string theory can include all older theories of physics, have led many physicists to believe that such a connection is possible. In particular, string theory is the first candidate for the theory of everything, a way to describe all the known natural forces (gravitational, electromagnetic, weak and strong) and matter (quarks and leptons) in a mathematically complete system. On the other hand, many detractors criticise string theory because it has not yet provided experimentally testable predictions.

Like any other quantum theory of gravity, it is widely believed that testing the theory experimentally would be prohibitively expensive, requiring feats of engineering on a solar-system scale. Although some critics concede that string theory is falsifiable in principle, they maintain that it is unfalsifiable for the foreseeable future, and so should not be called science.

String theory is of interest to many physicists because of the mathematics involved, and because of the large number of forms that the theories can take. String theory strongly suggests that spacetime has eleven dimensions,[1] as opposed to the usual three space and one time, but the theory can easily describe universes with four observable spacetime dimensions as well.[2]

String theories include objects more general than strings, called branes. The word brane, derived from "membrane", refers to a variety of interrelated objects, such as D-branes, black p-branes and Neveu-Schwarz 5-branes. These are typically extended objects that source differential form generalizations of the vector potential electromagnetic field. All such objects are known to be related to one-another by a variety of dualities. For example, the black hole-like black p-branes are identified with D-branes, upon which strings end, through Gauge-gravity duality. Research on this equivalence has led to new insights on quantum chromodynamics, the fundamental theory of the strong nuclear force.[3][4][5][6]

Contents

Overview

See also: Quantum gravity

String theory is a theory in which the electrons and quarks inside an atom are not 0-dimensional objects, but 1-dimensional strings. These string can move and vibrate, giving the observed particles their flavor, charge, mass and spin. The strings make closed loops unless they encounter surfaces, called D-branes, where they can open up into one dimensional lines. The endpoints of the string can't break off the D-brane, but they can slide around on it.

Levels of magnification:
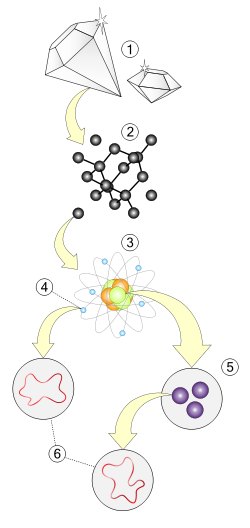
1. Macroscopic level - Matter
2. Molecular level
3. Atomic level - Protons, neutrons, and electrons
4. Subatomic level - Electron
5. Subatomic level - Quarks
6. String level

String theory is a theory of gravity, an extension of General Relativity, and the classical interpretation of the strings and branes is that they are quantum mechanical vibrating extended charged black holes. The overarching physical insight behind string theory is the holographic principle, which states that the description of the oscillations of the surface of a black hole must also describe the space-time around it. Holography demands that a low-dimensional theory describing the fluctuations of a horizon will end up describing everything that can fall through, which can be anything at all. So a theory of a black hole horizon is a theory of everything.

Finding even one consistent holographic description, a priori, seems like a long-shot, because it would be a disembodied nonlocal description of quantum gravity. In string theory, not only is there one such description, there are several different ones, each describing fluctuations of horizons with different charges and dimensions, and all of them logically fit together. So the same physical objects and interactions can be described by the fluctuations of one-dimensional black hole horizons, or by three-dimensional horizons, or by zero-dimensional horizons. The fact that these different descriptions describe the same physics is overwhelming evidence that string theory is consistent.

An ordinary astronomical black hole does not have a convenient holographic description, because it has a Hawking temperature. String theories are formulated on cold black holes, which are those which have as much charge as possible. The first holographic theory discovered described the scattering of one-dimensional strings, tiny loops of vibrating horizon charged with a two-form vector potential which makes a charged black hole a one-dimensional line. Fluctuations of this line horizon describe all matter, so every elementary particle can be described by a mode of oscillation of a very small segment or loop of string. The string-length is approximately the Planck length, but can be significantly bigger when the strings are weakly interacting.

All string theories predict the existence of degrees of freedom which are usually described as extra dimensions. Without fermions, bosonic strings can vibrate in a flat but unstable 26-dimensional space time. In a superstring theory with fermions, the weak-coupling (no-interaction) limit describes a flat stable 10-dimensional space time. Interacting superstring theories are best thought of as configurations of an 11 dimensional supergravity theory called M-theory where one or more of the dimensions are curled up so that the line-extended charged black holes become long and light.

Long light strings can vibrate at different resonant frequencies, and each resonant frequency describes a different type of particle.[7] So in string limits, any elementary particle should be thought of as a tiny vibrating line, rather than as a point. The string can vibrate in different modes just as a guitar string can produce different notes, and every mode appears as a different particle: electron, photon, gluon, etc.

The only way in which strings can interact is by splitting and combining in a smooth way. It is impossible to introduce arbitrary extra matter, like point particles which interact with strings by collisions, because the particles can fall into the black hole, so holography demands that it must show up as a mode of oscillation. The only way to introduce new matter is to find gravitational backgrounds where strings can scatter consistently, or to add boundary conditions, endpoints for the strings. Some of the backgrounds are called NS-branes, which are extreme-charged black hole sheets of different dimensions. Other charged black-sheet backgrounds are the D-branes, which have an alternate description as planes where strings can end and slide. When the strings are long and light, the branes are classical and heavy. In other limits where the strings become heavy, some of the branes can become light.

Since string theory is widely believed to be a consistent theory of quantum gravity, many hope that it correctly describes our universe, making it a theory of everything. There are known configurations which describe all the observed fundamental forces and matter but with a zero cosmological constant and some new fields. There are other configurations with different values of the cosmological constant, which are metastable but long-lived. This leads many to believe that there is at least one metastable solution which is quantitatively identical with the standard model, with a small cosmological constant, which contains dark matter and a plausible mechanism for inflation. It is not yet known whether string theory has such a solution, nor how much freedom the theory allows to choose the details. Because of this, string theory has not yet made practically falsifiable predictions that would allow it to be experimentally tested.

The full theory does not yet have a satisfactory definition in all circumstances, since the scattering of strings is most straightforwardly defined by a perturbation theory. The complete quantum mechanics of high dimensional branes is not easily defined, and the behavior of string theory in cosmological settings (time-dependent backgrounds) is not fully worked out. It is also not clear if there is any principle by which string theory selects its vacuum state, the space-time configuration which determines the properties of our Universe (see string theory landscape).

Basic properties

String theory can be formulated in terms of an action principle, either the Nambu-Goto action or the Polyakov action, which describes how strings move through space and time. In the absence of external interactions, string dynamics are governed by tension and kinetic energy, which combine to produce oscillations. The quantum mechanics of strings implies these oscillations take on discrete vibrational modes, the spectrum of the theory.

On distance scales larger than the string radius, each oscillation mode behaves as a different species of particle, with its mass, spin and charge determined by the strings dynamics. Splitting and recombinations of string correspond to particle emission and absorption, giving rise to the interactions between particles.

An analogy for strings' modes of vibration is a guitar string's production of multiple but distinct musical notes. In the analogy, different notes correspond to different particles. The only difference is the guitar is only 2-dimensional, you can strum it up, and down. In actuality the guitar strings would be every dimension, and the strings could vibrate in any direction. Meaning that the particles could move through not only our dimension, but other dimensions as well.

String theory includes both open strings, which have two distinct endpoints, and closed strings making a complete loop. The two types of string behave in slightly different ways, yielding two different spectra. For example, in most string theories, one of the closed string modes is the graviton, and one of the open string modes is the photon. Because the two ends of an open string can always meet and connect, forming a closed string, there are no string theories without closed strings.

The earliest string model, the bosonic string, incorporated only bosons. This model describes, in low enough energies, a quantum gravity theory, which also includes (if open strings are incorporated as well) gauge fields such as the photon (or, more generally, any gauge theory). However, this model has problems. Most importantly, the theory has a fundamental instability, believed to result in the decay (at least partially) of space-time itself. Additionally, as the name implies, the spectrum of particles contains only bosons, particles which, like the photon, obey particular rules of behavior. Roughly speaking, bosons are the constituents of radiation, but not of matter, which is made of fermions. Investigating how a string theory may include fermions in its spectrum led to the invention of supersymmetry, a mathematical relation between bosons and fermions. String theories which include fermionic vibrations are now known as superstring theories; several different kinds have been described, but all are now thought to be different limits of M-theory.

Some qualitative properties of quantum strings can be understood in a fairly simple fashion. For example, quantum strings have tension, much like regular strings made of twine; this tension is considered a fundamental parameter of the theory. The tension of a quantum string is closely related to its size. Consider a closed loop of string, left to move through space without external forces. Its tension will tend to contract it into a smaller and smaller loop. Classical intuition suggests that it might shrink to a single point, but this would violate Heisenberg's uncertainty principle. The characteristic size of the string loop will be a balance between the tension force, acting to make it small, and the uncertainty effect, which keeps it "stretched". Consequently, the minimum size of a string is related to the string tension.

Worldsheet

For more details on this topic, see Relationship between string theory and quantum field theory.

A point-like particle's motion may be described by drawing a graph of its position (in one or two dimensions of space) against time. The resulting picture depicts the worldline of the particle (its 'history') in spacetime. By analogy, a similar graph depicting the progress of a string as time passes by can be obtained; the string (a one-dimensional object — a small line — by itself) will trace out a surface (a two-dimensional manifold), known as the worldsheet. The different string modes (representing different particles, such as photon or graviton) are surface waves on this manifold.

A closed string looks like a small loop, so its worldsheet will look like a pipe or, more generally, a Riemannian surface (a two-dimensional oriented manifold) with no boundaries (i.e. no edge). An open string looks like a short line, so its worldsheet will look like a strip or, more generally, a Riemann surface with a boundary.

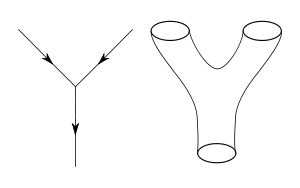
Interaction in the subatomic world: world lines of point-like particles in the Standard Model or a world sheet swept up by closed strings in string theory

Strings can split and connect. This is reflected by the form of their worldsheet (more accurately, by its topology). For example, if a closed string splits, its worldsheet will look like a single pipe splitting (or connected) to two pipes (often referred to as a pair of pants — see drawing at right). If a closed string splits and its two parts later reconnect, its worldsheet will look like a single pipe splitting to two and then reconnecting, which also looks like a torus connected to two pipes (one representing the ingoing string, and the other — the outgoing one). An open string doing the same thing will have its worldsheet looking like a ring connected to two strips.

Note that the process of a string splitting (or strings connecting) is a global process of the worldsheet, not a local one: locally, the worldsheet looks the same everywhere and it is not possible to determine a single point on the worldsheet where the splitting occurs. Therefore these processes are an integral part of the theory, and are described by the same dynamics that controls the string modes.

In some string theories (namely, closed strings in Type I and some versions of the bosonic string), strings can split and reconnect in an opposite orientation (as in a Möbius strip or a Klein bottle). These theories are called unoriented. Formally, the worldsheet in these theories is a non-orientable surface.

Dualities

Main articles: String duality, S-duality, T-duality, and U-duality

Before the 1990s, string theorists believed there were five distinct superstring theories: open type I, closed type I, closed type IIA, closed type IIB, and the two flavors of heterotic string theory (SO(32) and E8×E8)[8]. The thinking was that out of these five candidate theories, only one was the actual correct theory of everything, and that theory was the one whose low energy limit, with ten spacetime dimensions compactified down to four, matched the physics observed in our world today. It is now believed that this picture was incorrect and that the five superstring theories are connected to one another as if they are each a special case of some more fundamental theory (thought to be M-theory). These theories are related by transformations that are called dualities. If two theories are related by a duality transformation, it means that the first theory can be transformed in some way so that it ends up looking just like the second theory. The two theories are then said to be dual to one another under that kind of transformation. Put differently, the two theories are mathematically different descriptions of the same phenomena.

These dualities link quantities that were also thought to be separate. Large and small distance scales, as well as strong and weak coupling strengths, are quantities that have always marked very distinct limits of behavior of a physical system in both classical field theory and quantum particle physics. But strings can obscure the difference between large and small, strong and weak, and this is how these five very different theories end up being related. T-duality relates the large and small distance scales between string theories, whereas S-duality relates strong and weak coupling strengths between string theories. U-duality links T-duality and S-duality.

Before the "duality revolution" there were believed to be five distinct versions of string theory, plus the (unstable) bosonic and gluonic theories.

String theories
Type Spacetime dimensions
 Details
Bosonic 26 Only bosons, no fermions, meaning only forces, no matter, with both open and closed strings; major flaw: a particle with imaginary mass, called the tachyon, representing an instability in the theory.
I 10 Supersymmetry between forces and matter, with both open and closed strings; no tachyon; group symmetry is SO(32)
IIA 10 Supersymmetry between forces and matter, with closed strings and open strings bound to D-branes; no tachyon; massless fermions are non-chiral
IIB 10 Supersymmetry between forces and matter, with closed strings and open strings bound to D-branes; no tachyon; massless fermions are chiral
HO 10 Supersymmetry between forces and matter, with closed strings only; no tachyon; heterotic, meaning right moving and left moving strings differ; group symmetry is SO(32)
HE 10 Supersymmetry between forces and matter, with closed strings only; no tachyon; heterotic, meaning right moving and left moving strings differ; group symmetry is E8×E8

Note that in the type IIA and type IIB string theories closed strings are allowed to move everywhere throughout the ten-dimensional space-time (called the bulk), while open strings have their ends attached to D-branes, which are membranes of lower dimensionality (their dimension is odd — 1, 3, 5, 7 or 9 — in type IIA and even — 0, 2, 4, 6 or 8 — in type IIB, including the time direction).

Extra dimensions

Number of dimensions

An intriguing feature of string theory is that it involves the prediction of extra dimensions. The number of dimensions is not fixed by any consistency criterion, but flat spacetime solutions do exist in the so-called "critical dimension". Cosmological solutions exist in a wider variety of dimensionalities, and these different dimensions—more precisely different values of the "effective central charge", a count of degrees of freedom which reduces to dimensionality in weakly curved regimes—are related by dynamical transitions.[9]

Nothing in Maxwell's theory of electromagnetism or Einstein's theory of relativity makes this kind of prediction; these theories require physicists to insert the number of dimensions "by hand", and this number is fixed and independent of potential energy. String theory allows one to relate the number of dimensions to scalar potential energy. Technically, this happens because a gauge anomaly exists for every separate number of predicted dimensions, and the gauge anomaly can be counteracted by including nontrivial potential energy into equations to solve motion. Furthermore, the absence of potential energy in the "critical dimension" explains why flat spacetime solutions are possible.

This can be better understood by noting that a photon included in a consistent theory (technically, a particle carrying a force related to an unbroken gauge symmetry) must be massless. The mass of the photon which is predicted by string theory depends on the energy of the string mode which represents the photon. This energy includes a contribution from the Casimir effect, namely from quantum fluctuations in the string. The size of this contribution depends on the number of dimensions since for a larger number of dimensions, there are more possible fluctuations in the string position. Therefore, the photon in flat spacetime will be massless—and the theory consistent—only for a particular number of dimensions.[10]

When the calculation is done, the critical dimensionality is not four as one may expect (three axes of space and one of time). The subset of X is equal to the relation of photon fluxuations in a linear dimension. Flat space string theories are 26-dimensional in the bosonic case, while superstring and M-theories turn out to involve 10 or 11 dimensions for flat solutions. In bosonic string theories, the 26 dimensions come from the Polyakov equation.[11] Starting from any dimension greater than four, it is necessary to consider how these are reduced to four dimensional space-time.

Calabi-Yau manifold (3D projection)

Compact dimensions

Two different ways have been proposed to resolve this apparent contradiction. The first is to compactify the extra dimensions; i.e., the 6 or 7 extra dimensions are so small as to be undetectable by present day experiments.

To retain a high degree of supersymmetry, these compactification spaces must be very special, as reflected in their holonomy. A 6-dimensional manifold must have SU(3) structure, a particular case (torsionless) of this being SU(3) holonomy, making it a Calabi-Yau space, and a 7-dimensional manifold must have G2 structure, with G2 holonomy again being a specific, simple, case. Such spaces have been studied in attempts to relate string theory to the 4-dimensional Standard Model, in part due to the computational simplicity afforded by the assumption of supersymmetry. More recently, progress has been made constructing more realistic compactifications without the degree of symmetry of Calabi-Yau or G2 manifolds.

A standard analogy for this is to consider multidimensional space as a garden hose. If the hose is viewed from a sufficient distance, it appears to have only one dimension, its length. Indeed, think of a ball just small enough to enter the hose. Throwing such a ball inside the hose, the ball would move more or less in one dimension; in any experiment we make by throwing such balls in the hose, the only important movement will be one-dimensional, that is, along the hose. However, as one approaches the hose, one discovers that it contains a second dimension, its circumference. Thus, an ant crawling inside it would move in two dimensions (and a fly flying in it would move in three dimensions). This "extra dimension" is only visible within a relatively close range to the hose, or if one "throws in" small enough objects. Similarly, the extra compact dimensions are only "visible" at extremely small distances, or by experimenting with particles with extremely small wavelengths (of the order of the compact dimension's radius), which in quantum mechanics means very high energies (see wave-particle duality).

Brane-world scenario

Another possibility is that we are "stuck" in a 3+1 dimensional (i.e. three spatial dimensions plus the time dimension) subspace of the full universe. This subspace is supposed to be a D-brane, hence this is known as a braneworld theory. Some People believe that some combination of the two ideas — compactification and branes — will ultimately yield the most realistic theory.

Effect of the hidden dimensions

In either case, gravity acting in the hidden dimensions affects other non-gravitational forces such as electromagnetism. In fact, Kaluza's early work demonstrated that general relativity in five dimensions actually predicts the existence of electromagnetism. However, because of the nature of Calabi-Yau manifolds, no new forces appear from the small dimensions, but their shape has a profound effect on how the forces between the strings appear in our four-dimensional universe. In principle, therefore, it is possible to deduce the nature of those extra dimensions by requiring consistency with the standard model, but this is not yet a practical possibility. It is also possible to extract information regarding the hidden dimensions by precision tests of gravity, but so far these have only put upper limitations on the size of such hidden dimensions.

D-branes

Main article: D-brane

Another key feature of string theory is the existence of D-branes. These are membranes of different dimensionality (anywhere from a zero dimensional membrane — which is in fact a point — and up, including 2-dimensional membranes, 3-dimensional volumes and so on).

D-branes are defined by the fact that worldsheet boundaries are attached to them. Thus D-branes can emit and absorb closed strings; therefore they have mass (since they emit gravitons) and — in superstring theories — charge as well (since they emit closed strings which are gauge bosons).

From the point of view of open strings, D-branes are objects to which the ends of open strings are attached. The open strings attached to a D-brane are said to "live" on it, and they give rise to gauge theories "living" on it (since one of the open string modes is a gauge boson such as the photon). In the case of one D-brane there will be one type of a gauge boson and we will have an Abelian gauge theory (with the gauge boson being the photon). If there are multiple parallel D-branes there will be multiple types of gauge bosons, giving rise to a non-Abelian gauge theory.

D-branes are thus gravitational sources, on which a gauge theory "lives". This gauge theory is coupled to gravity (which is said to exist in the bulk), so that normally each of these two different viewpoints is incomplete.

Gauge-gravity duality

Gauge-gravity duality is a conjectured duality between a quantum theory of gravity in certain cases and gauge theory in a lower number of dimensions. This means that each predicted phenomenon and quantity in one theory has an analogue in the other theory, with a "dictionary" translating from one theory to the other.

Description of the duality

In certain cases the gauge theory on the D-branes is decoupled from the gravity living in the bulk; thus open strings attached to the D-branes are not interacting with closed strings. Such a situation is termed a decoupling limit.

In those cases, the D-branes have two independent alternative descriptions. As discussed above, from the point of view of closed strings, the D-branes are gravitational sources, and thus we have a gravitational theory on spacetime with some background fields. From the point of view of open strings, the physics of the D-branes is described by the appropriate gauge theory. Therefore in such cases it is often conjectured that the gravitational theory on spacetime with the appropriate background fields is dual (i.e. physically equivalent) to the gauge theory on the boundary of this spacetime (since the subspace filled by the D-branes is the boundary of this spacetime). So far, this duality has not been proven in any cases, so there is also disagreement among string theorists regarding how strong the duality applies to various models.

Examples and intuition

The most well-known example and the first one to be studied is the duality between Type IIB supergravity on AdS5 \times S5 (a product space of a five-dimensional Anti de Sitter space and a five-sphere) on one hand, and N = 4 supersymmetric Yang-Mills theory on the four-dimensional boundary of the Anti de Sitter space (either a flat four-dimensional spacetime R3,1 or a three-sphere with time S3 \times R).[12] This is known as the AdS/CFT correspondence, a name often used for Gauge / gravity duality in general.

This duality can be thought of as follows: suppose there is a spacetime with a gravitational source, for example an extremal black hole. When particles are far away from this source, they are described by closed strings (i.e. a gravitational theory, or usually supergravity). As the particles approach the gravitational source, they can still be described by closed strings; alternatively, they can be described by objects similar to QCD strings, which are made of gauge bosons (gluons) and other gauge theory degrees of freedom. So if one is able (in a decoupling limit) to describe the gravitational system as two separate regions — one (the bulk) far away from the source, and the other close to the source — then the latter region can also be described by a gauge theory on D-branes. This latter region (close to the source) is termed the near-horizon limit, since usually there is an event horizon around (or at) the gravitational source.

In the gravitational theory, one of the directions in spacetime is the radial direction, going from the gravitational source and away (towards the bulk). The gauge theory lives only on the D-brane itself, so it does not include the radial direction: it lives in a spacetime with one less dimension compared to the gravitational theory (in fact, it lives on a spacetime identical to the boundary of the near-horizon gravitational theory). Let us understand how the two theories are still equivalent:

The physics of the near-horizon gravitational theory involves only on-shell states (as usual in string theory), while the field theory includes also off-shell correlation function. The on-shell states in the near-horizon gravitational theory can be thought of as describing only particles arriving from the bulk to the near-horizon region and interacting there between themselves. In the gauge theory these are "projected" onto the boundary, so that particles which arrive at the source from different directions will be seen in the gauge theory as (off-shell) quantum fluctuations far apart from each other, while particles arriving at the source from almost the same direction in space will be seen in the gauge theory as (off-shell) quantum fluctuations close to each other. Thus the angle between the arriving particles in the gravitational theory translates to the distance scale between quantum fluctuations in the gauge theory. The angle between arriving particles in the gravitational theory is related to the radial distance from the gravitational source at which the particles interact: the larger the angle, the closer the particles have to get to the source in order to interact with each other. On the other hand, the scale of the distance between quantum fluctuations in a quantum field theory is related (inversely) to the energy scale in this theory. So small radius in the gravitational theory translates to low energy scale in the gauge theory (i.e. the IR regime of the field theory) while large radius in the gravitational theory translates to high energy scale in the gauge theory (i.e. the UV regime of the field theory).

A simple example to this principle is that if in the gravitational theory there is a setup in which the dilaton field (which determines the strength of the coupling) is decreasing with the radius, then its dual field theory will be asymptotically free, i.e. its coupling will grow weaker in high energies.

Contact with experiment

This branch of string theory may lead to new insights on quantum chromodynamics, a gauge theory which is the fundamental theory of the strong nuclear force. To this end, it is hoped that a gravitational theory dual to quantum chromodynamics will be found.[13]

In fact, a vague contact with experiment has already been claimed to have been achieved[3][4][5][6], though currently the alternative explanation for quark-gluon plasma behavior, Lattice QCD, is doing a much better job and has already made contact with experiments in various fields with good results,[14] though the computations are numerical rather than analytic. Other possible experiments for string theory have been proposed. One is the discovery of large cosmic strings in space, formed when the high energies in the Big Bang "stretched" some strings to astronomical proportions. Other possible avenues of experiment which could help provide evidence for string theory may take place at the newly built Large Hadron Collider. One is the measurement of the strength of gravity on a microscopic scale, which could provide evidence for extra dimensions; if gravitons (which are closed strings) leak off the membrane, at small scales the force of gravity should be much greater than at large scales where the gravitons would have ample chance to leak away into the bulk. The discovery of supersymmetry could also be considered evidence since string theory was the first theory to require it, though other theories have managed to incorporate supersymmetry as well. Also, the absence of supersymmetric particles at energies accessible to the LHC would not necessarily disprove string theory, since supersymmetry could exist but still be outside the accelerator's range.

Question mark2.svg
Unsolved problems in physics: Is there a string theory vacuum which exactly describes everything in our universe? Is it uniquely determined by low energy data?

Problems and controversy

Although string theory is an outgrowth of physics, some contend that string theory's current untestable status means that it should (strictly speaking) be classified as more of a mathematical framework. For a scientific theory to be valid it must be corroborated empirically, i.e. through experiment or observation. Few avenues for such contact with experiment have been claimed.[15] With the construction of the Large Hadron Collider in CERN some scientists hope to produce relevant data, though it is widely believed that any theory of quantum gravity would require much higher energies, higher by orders of magnitude[16], to probe directly. Moreover, string theory as it is currently understood has a huge number of equally possible solutions.[17] Thus it has been claimed by some scientists that string theory may not be falsifiable and may have no predictive power.[18][19][20][21] String theory does predict, at least perturbatively, that at sufficiently high energies—which are probably near the quantum gravity scale—the string-like nature of particles should be apparent. For example, there should be heavier copies of all particles corresponding to higher string harmonics. However, it is unclear what these energies are. In the limiting case, these energies would be one million billion (ten followed by fourteen zeros) times higher than those accessible in the newest particle accelerator, the LHC. String theory possesses many features of mathematical interest and naturally incorporates all the gross features of the Standard Model, such as non-abelian gauge groups and chiral fermions. But because the theory will be difficult to test in the foreseeable future, some theoretical physicists[22] have asked if it can be called a scientific theory, as it is not yet falsifiable in the sense of Popper.

It has also been suggested that string theory is better thought of as a framework for building models, in the same way that quantum field theory is a framework.[23]

String theory might not be truly fundamental in its present formulation because it is background-dependent — string theory describes perturbative expansions about fixed spacetime backgrounds. Although the theory is conceptually background-independent, as topology change is an established process in string theory, and the exchange of gravitons is equivalent to a change in the background, the mathematical execution of the theory relies on preselecting a background as a starting point for calculations. This is because, like many quantum field theories, much of string theory is still only formulated perturbatively (i.e., as a series of approximations rather than as an exact solution). Although nonperturbative techniques have progressed considerably — including conjectured complete definitions in space-times satisfying certain asymptotics — a full non-perturbative definition of the theory is still lacking. While some see background independence as a fundamental requirement of a theory of quantum gravity, particularly since General Relativity is already background independent, some string theorists disagree that background-independence should be a guiding principle; most hope that M-theory, or a non-perturbative treatment of string theory (such as string field theory) will turn out to be background-independent, giving as solutions the many different versions of string theory with the different backgrounds.

A central problem for string theory's relevant application in physics is that the best understood backgrounds of string theory preserve much of the supersymmetry of the underlying theory, which results in time-invariant space-times: currently string theory cannot deal well with time-dependent, cosmological backgrounds. However, several models have been proposed to explain supersymmetry breaking, such as the Randall-Sundrum model, which suggests that our universe's brane interacts with another brane which contains particles that break supersymmetry.

Another issue is that the vacuum structure of the theory, called the string theory landscape, is not well understood. As string theory is presently understood, it appears to contain a large number of distinct, meta-stable vacua, perhaps 10500 or more. Each of these corresponds to a different possible universe, with a different collection of particles and forces.[17] What principle, if any, can be used to select among these vacua is an open issue. While there are no known continuous parameters in the theory, there is a very large discretuum (coined in contradistinction to continuum) of possible universes, which may be radically different from each other. Some physicists believe this is a benefit of the theory, as it may allow a natural anthropic explanation of the observed values of physical constants, in particular the small value of the cosmological constant.[24][25] The argument is that most universes contain values for physical constants which lead to inhabitable universes (at least for humans), and we happen to live in the most "friendly" universe. This principle is already employed to explain the existence of life on earth as the result of a life-friendly orbit around the medium-sized sun among an infinite number of possible orbits (as well as a relatively stable location in the galaxy). However, the cosmological version of the anthropic principle remains highly controversial due to the difficulty (if not impossibility) of testing it; many do not accept it as scientific in the sense of Popper.

Following the appearance of two books claiming string theory is a failure,[18][21] a hot media debate evolved in 2007.[26][27].

"For more than a generation, physicists have been chasing a will-o’-the-wisp called string theory. The beginning of this chase marked the end of what had been three-quarters of a century of progress. Dozens of string-theory conferences have been held, hundreds of new Ph.D.s have been minted, and thousands of papers have been written. Yet, for all this activity, not a single new testable prediction has been made, not a single theoretical puzzle has been solved. In fact, there is no theory so far—just a set of hunches and calculations suggesting that a theory might exist. And, even if it does, this theory will come in such a bewildering number of versions that it will be of no practical use: a Theory of Nothing."[28]

S. James Gates, Jr., Ph.D. strongly opposes the idea that string theory would not be falsifiable: "So, the next time someone tells you that string theory is not testable, remind them of the AdS/CFT connection ..."[29]. The idea is that AdS/CFT permits the calculation of the coupling of the "constants" of the four forces (gravitation, electromagnetism, weak and strong nuclear forces). Namely, if the electroweak unification happens before the electroweakstrong unification, the supersymmetry model will be falsified. But, if all three "constants" meet each other at the same energy in a "point" wherein all three forces unite in a electroweakstrong unification (without passing first through a electroweak unification), supersymmetry will have resisted falsification[30]. Professor Gates suggests that the LHC will be used for testing AdS/CFT, namely to check if the electroweakstrong unification does happen as predicted, and if it does happen at the energy computed according to AdS/CFT[31].

History

Main article: History of string theory

Some of the structures reintroduced by string theory arose for the first time much earlier as part of the program of classical unification started by Albert Einstein. The first person to add a fifth dimension to general relativity was German mathematician Theodor Kaluza in 1919, who noted that gravity in five dimensions describes both gravity and electromagnetism in four. In 1926, the Swedish physicist Oskar Klein gave a physical interpretation of the unobservable extra dimension--- it is wrapped into a small circle. Einstein introduced a non-symmetric geometric tensor, while much later Brans and Dicke added a scalar component to gravity. These ideas would be revived within string theory, where they are demanded by consistency conditions.

String theory was originally developed during the late 1960s and early 1970s as a never completely successful theory of hadrons, the subatomic particles like the proton and neutron which feel the strong interaction. In the 1960s, Geoffrey Chew and Steven Frautschi discovered that the mesons make families called Regge trajectories with masses related to spins in a way that was later understood by Yoichiro Nambu and Leonard Susskind to be the relationship expected from rotating strings. Chew advocated making a theory for the interactions of these trajectories which did not presume that they were composed of any fundamental particles, but would construct their interactions from self-consistency conditions on the S-matrix. The S-matrix approach was started by Werner Heisenberg in the 1940s as a way of constructing a theory which did not rely on the local notions of space and time, which Heisenberg believed break down at the nuclear scale. While the scale was off by many orders of magnitude, the approach he advocated was ideally suited for a theory of quantum gravity.

Working with experimental data, R. Dolen, D. Horn and C. Schmidt developed some sum rules for hadron exchange. When a particle and antiparticle scatter, virtual particles can be exchanged in two qualitatively different ways. In the s-channel, the two particles annihilate to make temporary intermediate states which fall apart into the final state particles. In the t-channel, the particles exchange intermediate states by emission and absorption. In field theory, the two contributions add together, one giving a continuous background contribution, the other giving peaks at certain energies. In the data, it was clear that the peaks were stealing from the background--- the authors interpreted this as saying that the t-channel contribution was dual to the s-channel one, meaning both described the whole amplitude and included the other.

The result was widely advertised by Murray Gell-Mann, leading Gabriele Veneziano to construct a scattering amplitude which had the property of Dolen-Horn-Schmidt duality, later renamed world-sheet duality. The amplitude needed poles where the particles appear, on straight line trajectories, and there is a special mathematical function whose poles are evenly spaced on half the real line--- the Gamma function--- which was widely used in Regge theory. By manipulating combinations of Gamma functions, Veneziano was able to find a consistent scattering amplitude with poles on straight lines, with mostly positive residues, which obeyed duality and had the appropriate Regge scaling at high energy. The amplitude could fit near-beam scattering data as well as other Regge type fits, and had a suggestive integral representation which could be used for generalization.

Over the next years, hundreds of physicists worked to complete the bootstrap program for this model, with many surprises. Veneziano himself discovered that for the scattering amplitude to describe the scattering of a particle which appears in the theory, an obvious self-consistency condition, the lightest particle must be a tachyon. Miguel Virasoro and Joel Shapiro found a different amplitude now understood to be that of closed strings, while Ziro Koba and Holger Nielsen generalized Veneziano's integral representation to multiparticle scattering. Veneziano and Sergio Fubini introduced an operator formalism for computing the scattering amplitudes which was a forerunner of world-sheet conformal theory, while Virasoro understood how to remove the poles with wrong-sign residues using a constraint on the states. Claud Lovelace calculated a loop amplitude, and noted that there is an inconsistency unless the dimension of the theory is 26. Charles Thorn, Peter Goddard and Richard Brower went on to prove that there are no wrong-sign propagating states in dimensions less than or equal to 26.

In 1969 Yoichiro Nambu, Holger Bech Nielsen and Leonard Susskind recognized that the theory could be given a description in space and time in terms of strings. The scattering amplitudes were derived systematically from the action principle by Peter Goddard, Jeffrey Goldstone, Claudio Rebbi and Charles Thorn, giving a space-time picture to the vertex operators introduced by Veneziano and Fubini and a geometrical interpretation to the Virasoro conditions.

In 1970, Pierre Ramond added fermions to the model, which led him to formulate a two-dimensional supersymmetry to cancel the wrong-sign states. John Schwarz and André Neveu added another sector to the fermi theory a short time later. In the fermion theories, the critical dimension was 10. Stanley Mandelstam formulated a world sheet conformal theory for both the bose and fermi case, giving a two-dimensional field theoretic path-integral to generate the operator formalism.

In 1974, Tamiaki Yoneya discovered that all the known string theories included a massless spin-two particle which obeyed the correct Ward identities to be a graviton. John Schwarz and Joel Scherk came to the same conclusion and made the bold leap to suggest that string theory was a theory of gravity, not a theory of hadrons. They reintroduced Kaluza-Klein theory as a way of making sense of the extra dimensions. At the same time, quantum chromodynamics was recognized as the correct theory of hadrons, shifting the attention of physicists and apparently leaving the bootstrap program in the dustbin of history.

String theory eventually made it out of the dustbin, but for the following decade all work on the theory was completely ignored. Still, the theory continued to develop at a steady pace thanks the work of a handful of devotees. Ferdinando Gliozzi, Joel Scherk, and David Olive realized in 1976 that the original Ramond and Neveu Schwarz-strings were separately inconsistent and needed to be combined. The resulting theory did not have a tachyon, and was proven to have space-time supersymmetry by John Schwarz and Michael Green in 1981. The same year, Alexander Polyakov gave the theory a modern path integral formulation, and went on to develop conformal field theory extensively. In 1979, Daniel Friedan showed that the equations of motions of string theory, which are generalizations of the Einstein equations of General Relativity, emerge from the Renormalization group equations for the two-dimensional field theory. Schwarz and Green discovered T-duality, and constructed two different superstring theories--- IIA and IIB related by T-duality, and type I theories with open strings. The consistency conditions had been so strong, that the entire theory was nearly uniquely determined, with only a few discrete choices.

In the early 1980s, Edward Witten discovered that most theories of quantum gravity could not accommodate chiral fermions like the neutrino. This led him, in collaboration with Luiz Alvarez-Gaume to study violations of the conservation laws in gravity theories with anomalies, concluding that type I string theories were inconsistent. Green and Schwarz discovered a contribution to the anomaly that Witten and Alvarez-Gaume had missed, which restricted the gauge group of the type I string theory to be SO(32). In coming to understand this calculation, Edward Witten became convinced that string theory was truly a consistent theory of gravity, and he became a high-profile advocate. Following Witten's lead, between 1984 and 1986, hundreds of physicists started to work in this field, and this is sometimes called the first superstring revolution.

During this period, David Gross, Jeffrey Harvey, Emil Martinec, and Ryan Rohm discovered heterotic strings. The gauge group of these closed strings was two copies of E8, and either copy could easily and naturally include the standard model. Philip Candelas, Gary Horowitz, Andrew Strominger and Edward Witten found that the Calabi-Yau manifolds are the compactifications which preserve a realistic amount of supersymmetry, while Lance Dixon and others worked out the physical properties of orbifolds, distinctive geometrical singularities allowed in string theory. Cumrun Vafa generalized T-duality from circles to arbitrary manifolds, creating the mathematical field of mirror symmetry. David Gross and Vipul Periwal discovered that string perturbation theory was divergent in a way that suggested that new non-perturbative objects were missing.

In the 1990s, Joseph Polchinski discovered that the theory requires higher-dimensional objects, called D-branes and identified these with the black-hole solutions of supergravity. These were understood to be the new objects suggested by the perturbative divergences, and they opened up a new field with rich mathematical structure. It quickly became clear that D-branes and other p-branes, not just strings, formed the matter content of the string theories, and the physical interpretation of the strings and branes was revealed--- they are a type of black hole. Leonard Susskind had incorporated the holographic principle of Gerardus 't Hooft into string theory, identifying the long highly-excited string states with ordinary thermal black hole states. As suggested by 't Hooft, the fluctuations of the black hole horizon, the world-sheet or world-volume theory, describes not only the degrees of freedom of the black hole, but all nearby objects too.

In 1995, at the annual conference of string theorists at the University of Southern California (USC), Edward Witten gave a speech on string theory that essentially united the five string theories that existed at the time, and giving birth to a new 11-dimensional theory called M-theory. M-theory was also foreshadowed in the work of Paul Townsend at approximately the same time. The flurry of activity which began at this time is sometimes called the second superstring revolution.

During this period, Tom Banks, Willy Fischler Stephen Shenker and Leonard Susskind formulated a full holographic description of M-theory on IIA D0 branes, the first definition of string theory that was fully non-perturbative and a concrete mathematical realization of the holographic principle. Andrew Strominger and Cumrun Vafa calculated the entropy of certain configurations of D-branes and found agreement with the semi-classical answer for extreme charged black holes. Petr Horava and Edward Witten found the eleven-dimensional formulation of the heterotic string theories, showing that orbifolds solve the chirality problem. Witten noted that the effective description of the physics of D-branes at low energies is by a supersymmetric gauge theory, and found geometrical interpretations of mathematical structures in gauge theory that he and Nathan Seiberg had earlier discovered in terms of the location of the branes.

In 1997 Juan Maldacena noted that the low energy excitations of a theory near a black hole consist of objects close to the horizon, which for extreme charged black holes looks like an anti de Sitter space. He noted that in this limit the gauge theory describes the string excitations near the branes. So he hypothesized that string theory on a near-horizon extreme-charged black-hole geometry, an anti-deSitter space times a sphere with flux, is equally well described by the low-energy limiting gauge theory, the N=4 supersymmetric Yang-Mills theory. This hypothesis, complemented by converging work due to Steven Gubser, Igor Klebanov and Alexander Polyakov, is called the AdS/CFT correspondence and it is now well-accepted. It is a concrete realization of the holographic principle, which has far-reaching implications for black holes, locality and information in physics, as well as the nature of the gravitational interaction. Through this relationship, string theory has been shown to be related to gauge theories like quantum chromodynamics and this has led to more quantitative understanding of the behavior of hadrons, bringing string theory back to its roots.

See also

References

  1. ↑ M. J. Duff, James T. Liu and R. Minasian Eleven Dimensional Origin of String/String Duality: A One Loop Test Center for Theoretical Physics, Department of Physics, Texas A&M University
  2. ↑ Polchinski, Joseph (1998). String Theory, Cambridge University Press.
  3. ↑ 3.0 3.1 H. Nastase The RHIC fireball as a dual black hole BROWN-HET-1439, ArXiv: hep-th/0501068, January 2005,
  4. ↑ 4.0 4.1 H. Nastase More on the RHIC fireball and dual black holes BROWN-HET-1466, ArXiv: hep-th/0603176, March 2006,
  5. ↑ 5.0 5.1 H. Liu, K. Rajagopal, U. A. Wiedemann An AdS/CFT Calculation of Screening in a Hot Wind, MIT-CTP-3757, July 2006,
  6. ↑ 6.0 6.1 H. Liu, K. Rajagopal, U. A. Wiedemann Calculating the Jet Quenching Parameter from AdS/CFT, Phys.Rev.Lett.97:182301,2006
  7. ↑ To compare, the size of an atom is roughly 10-10 m and the size of a proton is 10-15 m. To imagine the Planck length: you can stretch along the diameter of an atom the same number of strings as the number of atoms you can line up to Proxima Centauri (the nearest star to Earth after the Sun). The tension of a string (8.9×1042 newtons) is about 1041 times the tension of an average piano string (735 newtons).
  8. ↑ S. James Gates, Jr., Ph.D., Superstring Theory: The DNA of Reality "Lecture 23 - Can I Have that Extra Dimension in the Window?", 0:04:54, 0:21:00.
  9. ↑ Simeon Hellerman, Ian Swanson: "Dimension-changing exact solutions of string theory". e-Print: hep-th/0612051; Ofer Aharony, Eva Silverstein: "Supercritical stability, transitions and (pseudo)tachyons". Physical Review D 75:046003, 2007. e-Print: hep-th/0612031
  10. ↑ The calculation of the number of dimensions can be circumvented by adding a degree of freedom which compensates for the "missing" quantum fluctuations. However, this degree of freedom behaves similar to spacetime dimensions only in some aspects, and the produced theory is not Lorentz invariant, and has other characteristics which don't appear in nature. This is known as the linear dilaton or non-critical string.
  11. ↑ "Quantum Geometry of Bosonic Strings – Revisited"
  12. ↑ Aharony, O.; S.S. Gubser, J. Maldacena, H. Ooguri, Y. Oz (2000). "Large N Field Theories, String Theory and Gravity" (subscription required). Phys. Rept. 323: 183–386. doi:10.1016/S0370-1573(99)00083-6. http://arxiv.org/abs/hep-th/9905111. . For other examples see: [1]
  13. ↑ For example: T. Sakai and S. Sugimoto, Low energy hadron physics in holographic QCD, Prog.Theor.Phys.113:843-882,2005, ArXiv: hep-th/0412141, December 2004
  14. ↑ See for example Recent Results of the MILC research program, taken from the MILC Collaboration homepage
  15. ↑ M. R. Douglas,Are There Testable Predictions of String Theory? February 2007 Texas A&M
  16. ↑ See e.g. E. Kiritsis, String theory in a nutshell. Introduction to Modern String theory, Princeton University Press, Princeton, N.Y. (2007)
  17. ↑ 17.0 17.1 S. Kachru, R. Kallosh, A. Linde and S. P. Trivedi, de Sitter Vacua in String Theory, Phys.Rev.D68:046005,2003
  18. ↑ 18.0 18.1 Peter Woit's Not Even Wrong weblog
  19. ↑ P. Woit (Columbia University) String theory: An Evaluation,February 2001, e-Print: physics/0102051
  20. ↑ P. Woit, Is String Theory Testable? INFN Rome March 2007
  21. ↑ 21.0 21.1 Lee Smolin's The Trouble With Physics webpage
  22. ↑ Prominent critics include Philip Anderson ("string theory is the first science in hundreds of years to be pursued in pre-Baconian fashion, without any adequate experimental guidance", New York Times, 4 January 2005), Sheldon Glashow ("there ain't no experiment that could be done nor is there any observation that could be made that would say, `You guys are wrong.' The theory is safe, permanently safe", NOVA interview), Lawrence Krauss ("String theory [is] yet to have any real successes in explaining or predicting anything measurable", New York Times, 8 November 2005), Peter Woit (see his blog, article and book "Not Even Wrong", ISBN 0-224-07605-1) and Carlo Rovelli (see his Dialog on Quantum Gravity)
  23. ↑ David Gross, Perspectives, String Theory: Achievements and Perspectives - A conference
  24. ↑ N. Arkani-Hamed, S. Dimopoulos and S. Kachru, Predictive Landscapes and New Physics at a TeV, SLAC-PUB-10928, HUTP-05-A0001, SU-ITP-04-44, January 2005
  25. ↑ L. Susskind The Anthropic Landscape of String Theory, February 2003
  26. ↑ John Baez and responses on the group weblog The n-Category Cafe
  27. ↑ John Baez weblog
  28. ↑ Unstrung: The New Yorker
  29. ↑ S. James Gates, Jr., Ph.D., Superstring Theory: The DNA of Reality "Lecture 21 - Can 4D Forces (without Gravity) Love Strings?", 0:26:06-0:26:21, cf. 0:24:05-0:26-24.
  30. ↑ Idem, "Lecture 19 - Do-See-Do and Swing your Superpartner Part II" 0:16:05-0:24:29.
  31. ↑ Idem, Lecture 21, 0:20:10-0:21:20.

Further reading

Popular books and articles

Textbooks

External links