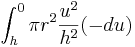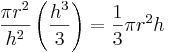Volume
The volume of any solid, plasma, vacuum or theoretical object is how much three-dimensional space it occupies, often quantified numerically. One-dimensional figures (such as lines) and two-dimensional shapes (such as squares) are assigned zero volume in the three-dimensional space. Volume is presented as ml or cm3.
Volumes of straight-edged and circular shapes are calculated using arithmetic formulae. Volumes of other curved shapes are calculated using integral calculus, by approximating the given body with a large amount of small cubes or concentric cylindrical shells, and adding the individual volumes of those shapes. The volume of irregularly shaped objects can be determined by displacement. If an irregularly shaped object is less dense than the fluid, you will need a weight to attach to the floating object. A sufficient weight will cause the object to sink. The final volume of the unknown object can be found by subtracting the volume of the attached heavy object and the total fluid volume displaced.
In differential geometry, volume is expressed by means of the volume form, and is an important global Riemannian invariant.
Volume and capacity are sometimes distinguished, with capacity being used for how much a container can hold (with contents measured commonly in liters or its derived units), and volume being how much space an object displaces (commonly measured in cubic meters or its derived units). The volume of a dispersed gas is the capacity of its container. If more gas is added to a closed container, the container expands (as in a balloon), the pressure inside the container increases, or both.
Volume and capacity are also distinguished in a capacity management setting, where capacity is defined as volume over a specified time period.
Volume is a fundamental parameter in thermodynamics and it is conjugate to pressure.
| Conjugate variables of thermodynamics |
|
|---|---|
| Pressure | Volume |
| (Stress) | (Strain) |
| Temperature | Entropy |
| Chem. potential | Particle no. |
Contents |
Volume formulas
| Common equations for volume: | ||
|---|---|---|
| Shape | Equation | Variables |
| A cube | 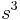 |
s = length of any side |
| A rectangular prism: | 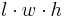 |
l = length, w = width, h = height |
| A cylinder (circular prism): | 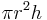 |
r = radius of circular face, h = height |
| Any prism that has a constant cross sectional area along the height**: | 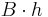 |
B = area of the base, h = height |
| A sphere: | 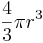 |
r = radius of sphere which is the integral of the Surface Area of a sphere |
| An ellipsoid: | 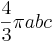 |
a, b, c = semi-axes of ellipsoid |
| A pyramid: | 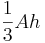 |
A = area of the base, h = height of pyramid |
| A cone (circular-based pyramid): |  |
r = radius of circle at base, h = distance from base to tip |
| Any figure (calculus required) |  |
h = any dimension of the figure, A(h) = area of the cross-sections perpendicular to h described as a function of the position along h. This will work for any figure if its cross-sectional area can be determined from h (no matter if the prism is slanted or the cross-sections change shape). |
(The units of volume depend on the units of length - if the lengths are in meters, the volume will be in cubic meters, etc)
The volume of a parallelepiped is the absolute value of the scalar triple product of the subtending vectors, or equivalently the absolute value of the determinant of the corresponding matrix.
The volume of any tetrahedron, given its vertices a, b, c and d, is (1/6)·|det(a−b, b−c, c−d)|, or any other combination of pairs of vertices that form a simply connected graph.
Volume measures: cooking
Traditional cooking measures for volume also include:
- teaspoon = 1/6 U.S. fluid ounce (about 4.929 mL)
- teaspoon = 1/6 Imperial fluid ounce (about 4.736 mL)
- teaspoon = 5 mL (metric)
- tablespoon = ½ U.S. fluid ounce or 3 teaspoons (about 14.79 mL)
- tablespoon = ½ Imperial fluid ounce or 3 teaspoons (about 14.21 mL)
- tablespoon = 15 mL or 3 teaspoons (metric)
- tablespoon = 5 fluidrams (about 17.76 mL) (British)
- cup = 8 U.S. fluid ounces or ½ U.S. liquid pint (about 237 mL)
- cup = 8 Imperial fluid ounces or ½ fluid pint (about 227 mL)
- cup = 250 mL (metric)
Relationship to density
The density of an object is defined as mass per unit volume.
The term specific volume is used for volume divided by mass. This is the reciprocal of the mass density, expressed in units such as cubic meters per kilogram.(m³·kg-1).
Volume formula derivation
| Shape | Volume formula derivation |
|---|---|
| Sphere | The volume of a sphere is the integral of infinitesimal circular slabs of thickness 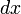 . .
The calculation for the volume of a sphere with center 0 and radius
Combining yields
|
| Cone | The volume of a cone is the integral of infinitesimal circular slabs of thickness 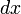 . .
The calculation for the volume of a cone of height
|
See also
- Area
- Conversion of units
- Density
- Orders of magnitude (volume)
- Length
- Mass
- Weight
- Dimensioning
- Dimensional weight
- Volume form
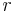 is as follows.
is as follows.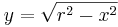
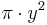

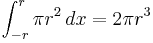
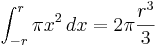

 . The volume of the sphere consists of layers of infinitesimal spherical slabs, and the sphere volume is equal to
. The volume of the sphere consists of layers of infinitesimal spherical slabs, and the sphere volume is equal to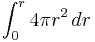 =
= 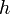 , whose base is centered at (0,0) with radius
, whose base is centered at (0,0) with radius 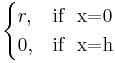 , and varying linearly in between -- that is,
, and varying linearly in between -- that is, 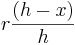
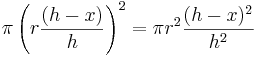
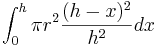
 gives an integral with reversed limits, and
gives an integral with reversed limits, and  : that is,
: that is,