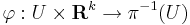Vector bundle

In mathematics, a vector bundle is a topological construction which makes precise the idea of a family of vector spaces parameterized by another space X (for example X could be a topological space, a manifold, or an algebraic variety): to every point x of the space X we associate (or "attach") a vector space V(x) in such a way that these vector spaces fit together to form another space of the same kind as X (e.g. a topological space, manifold, or algebraic variety), which is then called a vector bundle over X.
The simplest example is the case that the family of vector spaces is constant, i.e., there is a fixed vector space V such that V(x) = V for all x in X: in this case there is a copy of V for each x in X and these copies fit together to form the vector bundle X×V over X. Such vector bundles are said to be trivial. A more complicated (and prototypical) class of examples are the tangent bundles of smooth (or differentiable) manifolds: to every point of such a manifold we attach the tangent space to the manifold at that point. Tangent bundles are not, in general, trivial bundles: for example, the tangent bundle of the (two dimensional) sphere is not trivial by the Hairy ball theorem.
Vector bundles are almost always required to be locally trivial, however, which means they are examples of fiber bundles. Also, the vector spaces are usually vector spaces over the real or complex numbers, in which case the vector bundle is said to be a real or complex vector bundle (respectively). Complex vector bundles can be viewed as real vector bundles with additional structure. In the following, we focus on real vector bundles in the category of topological spaces.
Contents |
Definition and first consequences
Definition 1
A vector bundle is a fiber bundle, where the standard fiber V is a vector space, with structure group the general linear group of V.
Definition 2
A real vector bundle consists of:
- topological spaces X (base space) and E (total space)
- a continuous surjection π : E → X (bundle projection)
- for every x in X, the structure of a finite-dimensional real vector space on the fiber π -1({x})
where the following compatibility condition is satisfied: for every point in X, there is an open neighborhood U, a natural number k, and a homeomorphism
such that for all x ∈ U,
- πφ(x,v) = x for all vectors v in Rk, and
- the map v
 φ(x,v) is an isomorphism between the vector spaces Rk and π−1({x}).
φ(x,v) is an isomorphism between the vector spaces Rk and π−1({x}).
The open neighborhood U together with the homeomorphism φ is called a local trivialization of the vector bundle. The local trivialization shows that locally the map π "looks like" the projection of U × Rk on U.
Every fiber π−1({x}) is a finite-dimensional real vector space and hence has a dimension kx. The local trivializations show that the function x  kx is locally constant, and is therefore constant on each connected component of X. If kx is equal to a constant k on all of X, then k is called the rank of the vector bundle, and E is said to be a vector bundle of rank k. Vector bundles of rank 1 are called line bundles.
kx is locally constant, and is therefore constant on each connected component of X. If kx is equal to a constant k on all of X, then k is called the rank of the vector bundle, and E is said to be a vector bundle of rank k. Vector bundles of rank 1 are called line bundles.
The cartesian product X × Rk , equipped with the projection X × Rk → X, is called the trivial bundle of rank k over X.
Vector bundle morphisms
A morphism from the vector bundle π1 : E1 → X1 to the vector bundle π2 : E2 → X2 is given by a pair of continuous maps f : E1 → E2 and g : X1 → X2 such that
- g o π1 = π2 o f
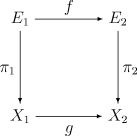
- for every x in X1, the map π1−1({x}) → π2−1({g(x)}) induced by f is a linear map between vector spaces.
Note that g is determined by f (because π1 is surjective), and f is then said to cover g.
The class of all vector bundles together with bundle morphisms forms a category. Restricting to vector bundles for which the spaces are manifolds (and the bundle projections are smooth maps) and smooth bundle morphisms we obtain the category of smooth vector bundles. Vector bundle morphisms are a special case of the notion of a bundle map between fiber bundles, and are also often called (vector) bundle homomorphisms.
A bundle homomorphism from E1 to E2 with an inverse which is also a bundle homomorphism (from E2 to E1) is called a (vector) bundle isomorphism, and then E1 and E2 are said to be isomorphic vector bundles. An isomorphism of a (rank k) vector bundle E over X with the trivial bundle (of rank k over X) is called a trivialization of E, and E is then said to be trivial (or trivializable). The definition of a vector bundle shows that any vector bundle is locally trivial.
We can also consider the category of all vector bundles over a fixed base space X. As morphisms in this category we take those morphisms of vector bundles whose map on the base space is the identity map on X. That is, bundle morphisms for which the following diagram commutes:
(Note that this category is not abelian; the kernel of a morphism of vector bundles is in general not a vector bundle in any natural way.)
A vector bundle morphism between vector bundles π1 : E1 → X1 and π2 : E2 → X2 covering a map g from X1 to X2 can also be viewed as a vector bundle morphism over X1 from E1 to the pullback bundle g*E2.
Sections and locally free sheaves

Given a vector bundle π : E → X and an open subset U of X, we can consider sections of π on U, i.e. continuous functions s : U → E with πs = idU. Essentially, a section assigns to every point of U a vector from the attached vector space, in a continuous manner. As an example, sections of the tangent bundle of a differential manifold are nothing but vector fields on that manifold.
Let F(U) be the set of all sections on U. F(U) always contains at least one element, namely the zero section: the function s that maps every element x of U to the zero element of the vector space π−1({x}). With the pointwise addition and scalar multiplication of sections, F(U) becomes itself a real vector space. The collection of these vector spaces is a sheaf of vector spaces on X.
If s is an element of F(U) and α : U → R is a continuous map, then αs (pointwise scalar multiplication) is in F(U). We see that F(U) is a module over the ring of continuous real-valued functions on U. Furthermore, if OX denotes the structure sheaf of continuous real-valued functions on X, then F becomes a sheaf of OX-modules.
Not every sheaf of OX-modules arises in this fashion from a vector bundle: only the locally free ones do. (The reason: locally we are looking for sections of a projection U × Rk → U; these are precisely the continuous functions U → Rk, and such a function is an k-tuple of continuous functions U → R.)
Even more: the category of real vector bundles on X is equivalent to the category of locally free and finitely generated sheaves of OX-modules. So we can think of the category of real vector bundles on X as sitting inside the category of sheaves of OX-modules; this latter category is abelian, so this is where we can compute kernels and cokernels of morphisms of vector bundles.
Operations on vector bundles
Most operations on vector spaces can be extended to vector bundles by performing the vector space operation fiberwise.
For example, if E is a vector bundle over X, then the there is a bundle E* over X, called the dual bundle, whose fiber at x∈X is the dual vector space (Ex)*. Formally E* can be defined as the set of pairs (x,φ), where x∈X and φ∈(Ex)*. The dual bundle is locally trivial because the dual space of the inverse of a local trivialization of E is a local trivialization of E*: the key point here, is that the operation of taking the dual vector space is functorial.
There are many functorial operations which can be performed on pairs of vector spaces (over the same field), and these extend straightforwardly to pairs of vector bundles E, F on X (over the given field). A few examples follow.
- The Whitney sum or direct sum bundle of E and F is a vector bundle
 over X whose fiber over x is the direct sum
over X whose fiber over x is the direct sum  of the vector spaces Ex and Fx.
of the vector spaces Ex and Fx.
- The tensor product bundle
 is defined in a similar way, using fiberwise tensor product of vector spaces.
is defined in a similar way, using fiberwise tensor product of vector spaces.
- The Hom-bundle Hom(E,F) is a vector bundle whose fiber at x is the space of linear maps from Ex to Fx (which is often denoted Hom(Ex,Fx) or L(Ex,Fx)). The Hom-bundle is so-called (and useful) because there is a bijection between vector bundle homomorphisms from E to F over X and sections of Hom(E,F) over X.
An operation of a different nature is the pullback bundle construction. Given a vector bundle E → Y and a continuous map f : X → Y one can "pull back" E to a vector bundle f*E over X. The fiber over a point x ∈ X is essentially just the fiber over f(x) ∈ Y.
Variants and generalizations
Vector bundles are special fiber bundles, loosely speaking those where the fibers are vector spaces.
Smooth vector bundles are defined by requiring that E and X be smooth manifolds, π : E → X be a smooth map, and the local trivialization maps φ be diffeomorphisms.
Replacing real vector spaces with complex ones, we obtain complex vector bundles. This is a special case of reduction of the structure group of a bundle. Vector spaces over other topological fields may also be used, but that is comparatively rare.
If we allow arbitrary Banach spaces in the local trivialization (rather than only Rn), we obtain Banach bundles.
K-theory
The K-theory group
- K(X)
of a manifold is defined as the abelian group generated by isomorphism classes [E] of (complex) vector bundles modulo the relation that whenever we have an exact sequence
- 0 → A → B → C → 0
then
- [B]=[A]+[C]
in topological K-theory. KO-theory is a version of this construction which considers real vector bundles. K-theory with compact supports can also be defined, as well as higher K-theory groups.
The famous periodicity theorem of Raoul Bott asserts that the K-theory of any space X is isomorphic to that of the Cartesian product
- X × S2,
where S2 denotes the 2-sphere.
In algebraic geometry, one considers the K-theory groups consisting of coherent sheaves on a scheme X, as well as the K-theory groups of vector bundles on the scheme with the above equivalence relation. The two constructs are the same provided that the underlying scheme is smooth.
See also
- Abelian category
- Grothendieck group
References
- Jurgen Jost, Riemannian Geometry and Geometric Analysis, (2002) Springer-Verlag, Berlin ISBN 3-540-42627-2 See section 1.5.
- Ralph Abraham and Jerrold E. Marsden, Foundations of Mechanics, (1978) Benjamin-Cummings, London ISBN 0-8053-0102-X See section 1.5.