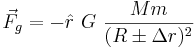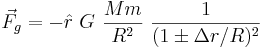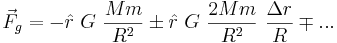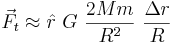Tidal force

Figure 1: Comet Shoemaker-Levy 9 after breaking up under the influence of Jupiter's tidal forces.

The tidal force is a secondary effect of the force of gravity and is responsible for the tides. It arises because the gravitational acceleration experienced by a large body is not constant across its diameter. One side of the body has greater acceleration than its center of mass, and the other side of the body has lesser acceleration.

Figure 1 shows Comet Shoemaker-Levy 9 after it had cracked up under the influence of Jupiter's tidal forces. The comet was falling into Jupiter, and the parts of the comet closest to Jupiter fell with a greater acceleration, due to the greater gravitational force. From the point of view of an observer riding on the comet, it would appear that the parts in front split off in the forward direction, while the parts in back split off in the backward direction. In reality, however, all parts of the comet were accelerating toward Jupiter, but at different rates.

Contents

Explanation

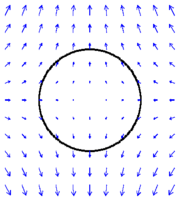
Figure 2: The Moon's (or Sun's) gravity differential field at the surface of the earth is known as the Tide Generating Force. This is the primary mechanism that drives tidal action and explains two tidal equipotential bulges, accounting for two high tides per day.

When a body (body 1) is acted on by the gravity of another body (body 2), the field can vary significantly on body 1 between the side of the body facing body 2 and the side facing away from body 2. Figure 2 shows the differential force of gravity on a spherical body (body 1) exerted by another body (body 2). These so called tidal forces cause strains on both bodies and may distort them or even, in extreme cases, break one or the other apart.[1] The Roche limit is the distance from a planet at which tidal effects would cause an object to disintegrate because the differential force of gravity from the planet overcomes the attraction of the parts of the object for one another.[2] These strains would not occur if the gravitational field is uniform, since a uniform field only causes the entire body to accelerate together in the same direction and at the same rate.

Effects of tidal forces

Figure 3: Saturn's rings are inside the orbits of its moons. Tidal forces prevented the material in the rings from coalescing gravitationally to form moons.[3]

In the case of an elastic sphere, the effect of a tidal force is to distort the shape of the body without any change in volume. The sphere becomes an ellipsoid, with two bulges, pointing towards and away from the other body. An elliptical distortion is approximately what happens to the Earth's oceans under the action of the Moon. The Earth and Moon rotate about their common center of mass or barycenter, and their gravitational attraction provides the centripetal force necessary to maintain this motion. To an observer on the Earth, very close to this barycenter, the situation is one of the Earth as body 1 acted upon by the gravity of the Moon as body 2. All parts of the Earth are subject to the Moon's gravitational forces, causing the water in the oceans to redistribute, forming bulges on the sides near the Moon and far from the Moon.[4]

When a body rotates while subject to tidal forces, internal friction results in the gradual dissipation of its rotational kinetic energy as heat. If the body is close enough to its primary, this can result in a rotation which is tidally locked to the orbital motion, as in the case of the Earth's moon. Tidal heating produces dramatic volcanic effects on Jupiter's moon Io.

Tidal forces contribute to ocean currents, which moderate global temperatures by transporting heat energy toward the poles. It has been suggested that in addition to variations of insolation associated with orbital forcing, harmonic beat variations in tidal forcing may contribute to climate changes.[5]

Tidal effects become particularly pronounced near small bodies of high mass, such as neutron stars or black holes, where they are responsible for the "spaghettification" of infalling matter. Tidal forces create the oceanic tide of Earth's oceans, where the attracting bodies are the Moon and, to a lesser extent, the Sun.

Tidal forces are also responsible for tidal locking and tidal acceleration.

Mathematical treatment

For a given (externally generated) gravitational field, the tidal acceleration at a point with respect to a body is obtained by vectorially subtracting the gravitational acceleration at the center of the body from the actual gravitational acceleration at the point. Correspondingly, the term tidal force is used to describe the forces due to tidal acceleration. Note that for these purposes the only gravitational field considered is the external one; the gravitational field of the body (as shown in the graphic) is not relevant.

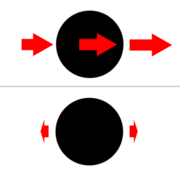
Figure 4: Graphic of tidal forces; the gravity field is generated by a body to the right. The top picture shows the gravitational forces; the bottom shows their residual once the field of the sphere is subtracted; this is the tidal force. See Figure 5 for a more exact version
Figure 5: More exact calculation of tidal forces; this figure is rotated 90° clockwise from Figure 4 (the gravitational body is below the figure).

Tidal acceleration does not require rotation or orbiting bodies; e.g. the body may be freefalling in a straight line under the influence of a gravitational field while still being influenced by (changing) tidal acceleration.

Newton's law of universal gravitation states that a particle of mass m a distance r from the center of a sphere of mass M feels a force of:

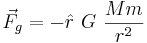\vec F_g = - \hat r ~ G ~ \frac{M m}{r^2},

where 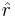\hat r is a unit vector pointing from the body M to the particle m.

Extending the description of m to a small body with spatial extent, suppose that R is the inter-object distance -- the distance from the center of M to the center of m, and let ∆r be the radius of m in the direction pointing towards M. Hence the points on the surface of m are located at distance 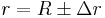r = R \pm \Delta r from the centre of M. Using the above equation, and ignoring the small contribution due to m's own mass, we have the gravitational force at these points as:

\vec F_g = - \hat r ~ G ~ \frac{M m}{(R \pm \Delta r)^2}

Pulling out the R² term from the denominator gives:

\vec F_g = - \hat r ~ G ~ \frac{M m}{R^2} ~ \frac{1}{(1 \pm \Delta r / R)^2}

The Maclaurin series of 1/(1 + x)² is 1 - 2 x + 3 x² - ..., which gives a series expansion of:

\vec F_g = - \hat r ~ G ~ \frac{M m}{R^2} \pm \hat r ~ G ~ \frac{2 M m }{R^2} ~ \frac{\Delta r}{R} \mp ...

The first term is the traditional gravitational force; all other terms are tidal force terms. Generally, the first is much more significant than the other terms, giving:

\vec F_t \approx \hat r ~ G ~ \frac{2 M m }{R^2} ~ \frac{\Delta r}{R}

The tidal forces can also be calculated away from the axis connecting the bodies, requiring a vector calculation of forces. In the plane perpendicular to the axis, the tidal force is directed inwards, and its magnitude is 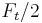F_t/2 in linear approximation as in Figure 5.

See also

References

  1. ↑ R Penrose (1999). The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics. Oxford University Press. p. 264. ISBN 0192861980. http://books.google.com/books?id=oI0grArWHUMC&pg=PA264&vq=tidal&dq=tidal+force&lr=&as_brr=0&source=gbs_search_s&sig=ACfU3U3N2jyScOSJZu-GxBiQrTnEiaL5QA. 
  2. ↑ Thérèse Encrenaz, J -P Bibring, M Blanc (2003). The Solar System. Springer. p. 16. ISBN 3540002413. http://books.google.com/books?id=Je61Y7UbqWgC&pg=PA16&vq=tide&dq=tidal+force&lr=&as_brr=0&source=gbs_search_s&sig=ACfU3U1a7gm97Sow1S17TnMtjsMYdSk1VQ#PPA16,M1. 
  3. ↑ R. S. MacKay, J. D. Meiss (1987). Hamiltonian Dynamical Systems: A Reprint Selection. CRC Press. p. 36. ISBN 0852742053. http://books.google.com/books?id=uTeqNsyj86QC&pg=PA36&dq=tidal+force&lr=&as_brr=0&sig=ACfU3U3CCqcDH2j1rRu64wbsCZyHHdCGMw. 
  4. ↑ Rollin A Harris (1920). The Encyclopedia Americana: A Library of Universal Knowledge (Vol. 26 ed.). Encyclopedia Americana Corp.. p. pp.611-617. http://books.google.com/books?id=r8BPAAAAMAAJ&pg=PA612&dq=tidal+force&lr=&as_brr=0#PPA612,M1. 
  5. ↑ "Millennial Climate Variability: Is There a Tidal Connection?".

External links