Theory of computation

The theory of computation is the branch of computer science that deals with whether and how efficiently problems can be solved on a model of computation, using an algorithm. The field is divided into two major branches: computability theory and complexity theory, but both branches deal with formal models of computation.

In order to perform a rigorous study of computation, computer scientists work with a mathematical abstraction of computers called a model of computation. There are several models in use, but the most commonly examined is the Turing machine. A Turing machine can be thought of as a desktop PC with a potentially infinite memory capacity, though it can only access this memory in small discrete chunks. Computer scientists study the Turing machine because it is simple to formulate, can be analyzed and used to prove results, and because it represents what many consider the most powerful possible "reasonable" model of computation. It might seem that the potentially infinite memory capacity is an unrealizable attribute, but any decidable problem solved by a Turing machine will always require only a finite amount of memory. So in principle, any problem that can be solved (decided) by a Turing machine can be solved by a computer that has a bounded amount of memory.

Contents 1 Computability theory 2 Complexity theory 3 Other formal definitions of computation 4 See also 5 Further reading 6 External links

Computability theory

Main article: Computability theory (computer science)

Computability theory deals primarily with the question of whether a problem is solvable at all on a computer. The statement that the halting problem cannot be solved by a Turing machine is one of the most important results in computability theory, as it is an example of a concrete problem that is both easy to formulate and impossible to solve using a Turing machine. Much of computability theory builds on the halting problem result.

The next important step in computability theory was the Rice's theorem, which states that for all non-trivial properties of partial functions, it is undecidable whether a Turing machine computes a partial function with that property.

Computability theory is closely related to the branch of mathematical logic called recursion theory, which removes the restriction of studying only models of computation which are close to physically realizable. Many mathematicians and Computational theorists who study recursion theory will refer to it as computability theory. There is no real difference between the fields other than whether a researcher working in this area has his or her office in the computer science or mathematics field.

Complexity theory

Main article: Computational complexity theory

Complexity theory considers not only whether a problem can be solved at all on a computer, but also how efficiently the problem can be solved. Two major aspects are considered: time complexity and space complexity, which are respectively how many steps does it take to perform a computation, and how much memory is required to perform that computation.

In order to analyze how much time and space a given algorithm requires, computer scientists express the time or space required to solve the problem as a function of the size of the input problem. For example, finding a particular number in a long list of numbers becomes harder as the list of numbers grows larger. If we say there are 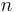numbers in the list, then if the list is not sorted or indexed in any way we may have to look at every number in order to find the number we're seeking. We thus say that in order to solve this problem, the computer needs to perform a number of steps that grows linearly in the size of the problem.

To simplify this problem, computer scientists have adopted Big O notation, which allows functions to be compared in a way that ensures that particular aspects of a machine's construction do not need to be considered, but rather only the asymptotic behavior as problems become large. So in our previous example we might say that the problem requires 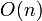steps to solve.

Perhaps the most important open problem in all of computer science is the question of whether a certain broad class of problems denoted NP can be solved efficiently. This is discussed further at Complexity classes P and NP.

Other formal definitions of computation

Aside from a Turing machine, other equivalent (See: Church-Turing thesis) models of computation are in use.

lambda calculus

A computation consists of an initial lambda expression (or two if you want to separate the function and its input) plus a finite sequence of lambda terms, each deduced from the preceding term by one application of Beta reduction.

Combinatory logic

is a concept which has many similarities to 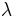-calculus, but also important differences exist (e.g. fixed point combinator Y has normal form in combinatory logic but not in 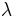-calculus). Combinatory logic was developed with great ambitions: understanding the nature of paradoxes, making foundations of mathematics more economic (conceptually), eliminating the notion of variables (thus clarifying their role in mathematics).

mu-recursive functions

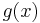a computation consists of a mu-recursive function, i.e. its defining sequence, any input value(s) and a sequence of recursive functions appearing in the defining sequence with inputs and outputs. Thus, if in the defining sequence of a recursive function the functions and 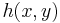appear, then terms of the form 'g(5)=7' or 'h(3,2)=10' might appear. Each entry in this sequence needs to be an application of a basic function or follow from the entries above by using composition, primitive recursion or mu recursion. For instance if 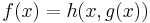, then for 'f(5)=3' to appear, terms like 'g(5)=6' and 'h(3,6)=3' must occur above. The computation terminates only if the final term gives the value of the recursive function applied to the inputs.

Markov algorithm

a string rewriting system that uses grammar-like rules to operate on strings of symbols.

Register machine

is a theoretically interesting idealization of a computer. There are several variants. In most of them, each register can hold a natural number (of unlimited size), and the instructions are simple (and few in number), e.g. only decrementation (combined with conditional jump) and incrementation exist (and halting). The lack of the infinite (or dynamically growing) external store (seen at Turing machines) can be understood by replacing its role with Gödel numbering techniques: the fact that each register holds a natural number allows the possibility of representing a complicated thing (e.g. a sequence, or a matrix etc.) by an appropriate huge natural number — unambiguity of both representation and interpretation can be established by number theoretical foundations of these techniques.

P′′

Like Turing machines, P′′ uses an infinite tape of symbols (without random access), and a rather minimalistic set of instructions. But these instructions are very different, thus, unlike Turing machines, P′′ does not need to maintain a distinct state, because all “memory-like” functionality can be provided only by the tape. Instead of rewriting the current symbol, it can perform a modular arithmetic incrementation on it. P′′ has also a pair of instructions for a cycle, inspecting the blank symbol. Despite its minimalistic nature, it has become the parental formal language of an implemented and (for entertainment) used programming language called Brainfuck.

In addition to the general computational models, some simpler computational models are useful for special, restricted applications. Regular expressions, for example, specify string patterns in many contexts, from office productivity software to programming languages. Another formalism mathematically equivalent to regular expressions, Finite automata are used in circuit design and in some kinds of problem-solving. Context-free grammars specify programming language syntax. Non-deterministic pushdown automata are another formalism equivalent to context-free grammars. Primitive recursive functions are a defined subclass of the recursive functions.

Different models of computation have the ability to do different tasks. One way to measure the power of a computational model is to study the class of formal languages that the model can generate; in such a way to the Chomsky hierarchy of languages is obtained.

See also

• Introduction to Automata Theory, Languages, and Computation

Further reading

• S. Barry Cooper (2004). Computability Theory. Chapman and Hall/CRC. ISBN 1-58488-237-9. 
• Richard L. Epstein and Walter A. Carnielli (2000). Computability: Computable Functions, Logic, and the Foundations of Mathematics, with Computability: A Timeline (2nd ed.). Wadsworth/Thomson Learning. ISBN 0-534-54644-7. 
• Michael Sipser (2006). Introduction to the Theory of Computation 2ed. PWS Publishing. ISBN 0-534-94728-X.  Part Two: Computability Theory, chapters 3–6, pp.123–222.
• Eitan Gurari (1989). An Introduction to the Theory of Computation. Computer Science Press. ISBN 0-7167-8182-4. 
• Hein, James L. (1996) Theory of Computation. Sudbury, MA: Jones & Bartlett. ISBN 978-0867204971 A gentle introduction to the field, appropriate for second-year undergraduate computer science students.
• Hopcroft, John E., and Jeffrey D. Ullman (2006). Introduction to Automata Theory, Languages, and Computation. 3rd ed Reading, MA: Addison-Wesley. ISBN 978-0321455369 One of the standard references in the field.
• Taylor, R. Gregory (1998). Models of Computation and Formal Languages. New York: Oxford University Press. ISBN 978-0195109832 An unusually readable textbook, appropriate for upper-level undergraduates or beginning graduate students.
• Hartley Rogers, Jr (1987). Theory of Recursive Functions and Effective Computability, MIT Press. ISBN 0-262-68052-1
• Lewis, F. D. (2007). Essentials of theoretical computer science A nice textbook covering the topics of formal languages, automata and grammars. The emphasis appears to be on presenting an overview of the results and their applications rather than providing proofs of the results.

External links

• Computability Logic - A theory of interactive computation. The main web source on this subject.