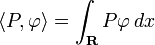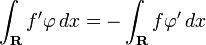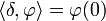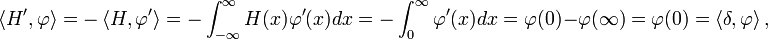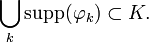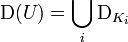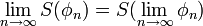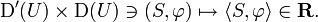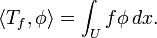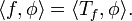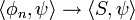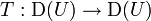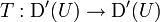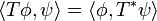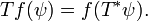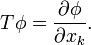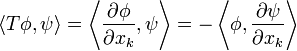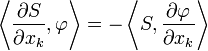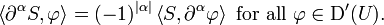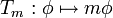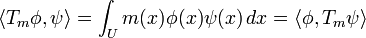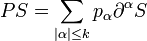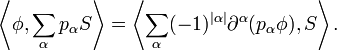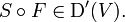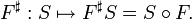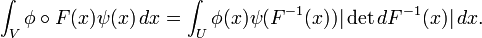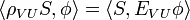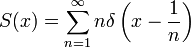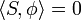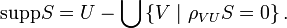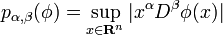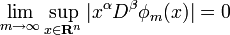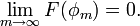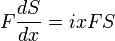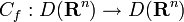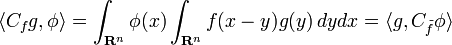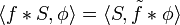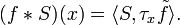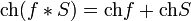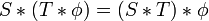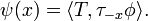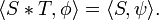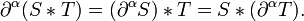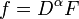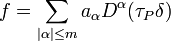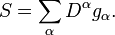Distribution (mathematics)
In mathematical analysis, distributions (also known as generalized functions) are objects which generalize functions and probability distributions. They extend the concept of derivative to all integrable functions and beyond, and are used to formulate generalized solutions of partial differential equations. They are important in physics and engineering where many non-continuous problems naturally lead to differential equations whose solutions are distributions, such as the Dirac delta distribution.
"Generalized functions" were introduced by Sergei Sobolev in 1935. They were independently introduced in the late 1940s by Laurent Schwartz, who developed a comprehensive theory of distributions.
Basic idea
The basic idea is to identify functions with abstract linear functionals on a space of unproblematic test functions (conventional and well-behaved functions). Operators on distributions can be understood by moving them to the test function.
For example, let
- f : R → R
be a locally integrable function, and let
- φ : R → R
be a smooth (that is, infinitely differentiable) function with compact support (i.e., identically zero outside of some bounded set). The function φ is the "test function." We then set
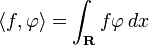 .
.
This is a real number which linearly and continuously depends on φ. One can therefore think of the function f as a continuous linear functional on the space which consists of all the "test functions" φ.
Similarly, if P is a probability distribution on the reals and φ is a test function, then
is a real number that continuously and linearly depends on φ: probability distributions can thus also be viewed as continuous linear functionals on the space of test functions. This notion of "continuous linear functional on the space of test functions" is therefore used as the definition of a distribution.
Such distributions may be multiplied with real numbers and can be added together, so they form a real vector space. In general it is not possible to define a multiplication for distributions, but distributions may be multiplied with infinitely differentiable functions.
To define the derivative of a distribution, we first consider the case of a differentiable and integrable function f : R → R. If φ is a test function, then we have
using integration by parts (note that φ is zero outside of a bounded set and that therefore no boundary values have to be taken into account). This suggests that if S is a distribution, we should define its derivative S' by
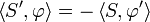 .
.
It turns out that this is the proper definition; it extends the ordinary definition of derivative, every distribution becomes infinitely differentiable and the usual properties of derivatives hold.
Example: The Dirac delta (so-called Dirac delta function) is the distribution defined by
It is the derivative of the Heaviside step function: For any test function 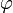 ,
,
so  .
.  because of compact support. Similarly, the derivative of the Dirac delta is the distribution
because of compact support. Similarly, the derivative of the Dirac delta is the distribution
This latter distribution is our first example of a distribution which is neither a function nor a probability distribution.
Test functions and distributions
In the sequel, real-valued distributions on an open subset U of Rn will be formally defined. With minor modifications, one can also define complex-valued distributions, and one can replace Rn by any (paracompact) smooth manifold.
The first object to define is the space D(U) of test functions on U. Once this is defined, it is then necessary to equip it with a topology by defining the limit of a sequence of elements of D(U). The space of distributions will then be given as the space of continuous linear functionals on D(U).
Test function space
The space D(U) of test functions on U is defined as follows. A function φ : U → R is said to have compact support if there exists a compact subset K of U such that φ(x) = 0 for all x in U \ K. The elements of D(U) are the infinitely differentiable functions φ : U → R with compact support — also known as bump functions. This is a real vector space. It can be given a topology by defining the limit of a sequence of elements of D(U). A sequence (φk) in D(U) is said to converge to φ ∈ D(U) if the following two conditions hold (Gelfand & Shilov 1966-1968, v. 1, §1.2):
- There is a compact set K ⊂ U containing the supports of all φk:
- For each multiindex α, the sequence of partial derivatives Dαφk tends uniformly to Dαφ.
With this definition, D(U) becomes a complete locally convex topological vector space satisfying the Heine-Borel property (Rudin 1991, §6.4-5). If Ui is a countable nested family of open subsets of U with compact closures  , then
, then
where DKi is the set of all smooth functions with support lying in Ki. The topology on D(U) is the final topology of the family of nested metric spaces DKi and so D(U) is an LF-space. The topology is not metrizable by the Baire category theorem, since D(U) is the union of subspaces of the first category in D(U) (Rudin 1991, §6.9).
Distributions
A distribution on U is a linear functional S : D(U) → R with values in R (or C), such that
for any convergent sequence φn in D(U). The space of all distributions on U is denoted by D'(U). Equivalently, the vector space D'(U) is the continuous dual space of the topological vector space D(U).
The dual pairing between a distribution S in D′(U) and a test function φ in D(U) is denoted using angle brackets thus:
Equipped with the weak-* topology, the space D'(U) is a locally convex topological vector space. In particular, a sequence (Sk) in D'(U) converges to a distribution S if and only if
for all test functions φ. This is the case if and only if Sk converges uniformly to S on all bounded subsets of D(U). (A subset E of D(U) is bounded if there exists a compact subset K of U and numbers dn such that every φ in E has its support in K and has its n-th derivatives bounded by dn.)
Functions as distributions
The function ƒ : U → R is called locally integrable if it is Lebesgue integrable over every compact subset K of U. This is a large class of functions which includes all continuous functions and all Lp functions. The topology on D(U) is defined in such a fashion that any locally integrable function ƒ yields a continuous linear functional on D(U) — that is, an element of D′(U) — denoted here by Tƒ, whose value on the test function φ is given by the Lebesgue integral:
Conventionally, one abuses notation by identifying Tƒ with ƒ, provided no confusion can arise, and thus the pairing between ƒ and φ is often written
If ƒ and g are two locally integrable functions, then the associated distributions Tƒ and Tg are equal the same element of D'(U) if and only if ƒ and g are equal almost everywhere (see, for instance, Hörmander (1983, Theorem 1.2.5)). In a similar manner, every Radon measure μ on U defines an element of D'(U) whose value on the test function φ is ∫φ dμ. As above, it is conventional to abuse notation and write the pairing between a Radon measure μ and a test function φ as 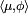 . Conversely, essentiallly by the Riesz representation theorem, every distribution which is non-negative on non-negative functions is of this form for some (positive) Radon measure.
. Conversely, essentiallly by the Riesz representation theorem, every distribution which is non-negative on non-negative functions is of this form for some (positive) Radon measure.
The test functions are themselves locally integrable, and so define distributions. As such they are dense in D'(U) with respect to the topology on D'(U) in the sense that for any distribution S ∈ D'(U), there is a sequence φn ∈ D(U) such that
for all ψ ∈ D(U). This follows at once from the Hahn-Banach theorem, since by an elementary fact about weak topologies the dual of D'(U) with its weak-* topology is the space D(U) (Rudin 1991, Theorem 3.10). This can also be proven more constructively by a convolution argument.
Operations on distributions
Many operations which are defined on smooth functions with compact support can also be defined for distributions. In general, if
is a linear mapping of vector spaces which is continuous with respect to the weak-* topology, then it is possible to extend T to a mapping
by passing to the limit. (This approach works for more general non-linear mappings as well, provided they are assumed to be uniformly continuous.)
In practice, however, it is more convenient to define operations on distributions by means of the transpose (or adjoint transformation) (Strichartz 1994, §2.3; Treves 1967). If T : D(U) → D(U) is a continuous linear operator, then the transpose is an operator T* : D(U) → D(U) such that
for all φ, ψ ∈ D(U). If such an operator T* exists, and is continuous, then the original operator T may be extended to distributions by defining
Differentiation
If T : D(U) → D(U) is given by the partial derivative
By integration by parts, if φ and ψ are in D(U), then
so that T* = −T. This is a continuous linear transformation D(U) → D(U). So, if S ∈ D'(U) is a distribution, then the partial derivative of S with respect to the coordinate xk is defined by the formula
for all test functions φ. In this way, every distribution is infinitely differentiable, and the derivative in the direction xk is a linear operator on D′(U). In general, if α = (α1, ..., αn) is an arbitrary multi-index and ∂α denotes the associated mixed partial derivative operator, the mixed partial derivative ∂αS of the distribution S ∈ D′(U) is defined by
Differentiation of distributions is a continuous operator on D'(U); this is an important and desirable property that is not shared by most other notions of differentiation.
Multiplication by a smooth function
If m : U → R is an infinitely differentiable function and S is a distribution on U, then the product mS is defined by (mS)(φ) = S(mφ) for all test functions φ. This definition coincides with the transpose transformation of
for φ ∈ D(U). Then, for any test function ψ
so that Tm* = Tm. Multiplication of a distribution S by the smooth function m is therefore defined by
Under multiplication by smooth functions, D'(U) is a module over the ring C∞(D). With this definition of multiplication by a smooth function, the ordinary product rule of calculus remains valid. However, a number of unusual identities also arise. For example, the Dirac delta distribution δ is defined on R by 〈δ, φ〉 = φ(0), and its derivative is given by 〈δ', φ〉 = −〈δ, φ'〉 = −φ'(0). However, the product mδ' is the distribution
This definition of multiplication also makes it possible to define the operation of a linear differential operator with smooth coefficients on a distribution. A linear differential operator takes a distribution S ∈ D'(U) to another distribution given by a sum of the form
where the coefficients pα are smooth functions in U. If P is a given differential operator, then the minimum integer k for which such an expansion holds for every distribution S is called the order of P. The transpose of P is given by
The space D'(U) is a D-module with respect to the action of the ring of linear differential operators.
Composition with a smooth function
Let S be a distribution on an open set U ⊂ Rn. Let V be an open set in Rn, and F : V → U. Then provided F is a submersion, it is possible to define
This is the composition of the distribution S with F, and is also called the pullback of S along F, sometimes written
The pullback is often denoted F*, but this notation risks confusion with the above use of '*' to denote the transpose of a linear mapping.
The condition that F be a submersion is equivalent to the requirement that the Jacobian derivative dF(x) of F is a surjective linear map for every x ∈ V. A necessary (but not sufficient) condition for extending F# to distributions is that F be an open mapping (Hörmander 1983, Theorem 6.1.1). The inverse function theorem ensures that a submersion satisfies this condition.
If F is a submersion, then F# is defined on distributions by finding the transpose map. Uniqueness of this extension is guaranteed since F# is a continuous linear operator on D(U). Existence, however, requires using the change of variables formula, the inverse function theorem (locally) and a partition of unity argument; see Hörmander (1983, Theorem 6.1.2).
In the special case when F is a diffeomorphism from an open subset V of Rn onto an open subset U of Rn change of variables under the integral gives
In this particular case, then, F# is defined by the transpose formula:
Localization of distributions
There is no way to define the value of a distribution in D'(U) at a particular point of U. However, as is the case with functions, distributions on U restrict to give distributions on open subsets of U. Furthermore, distributions are locally determined in the sense that a distribution on all of U can be assembled from a distribution on an open cover of U satisfying some compatibility conditions on the overlap. Such a structure is known as a sheaf
Restriction
Let U and V be open subsets of Rn with V ⊂ U. Let EVU : D(V) → D(U) be the operator which extends by zero a given smooth function compactly supported in V to a smooth function compactly supported in U. Then the restriction mapping ρVU is defined to be the transpose of EVU. Thus for any distribution S ∈ D'(U), the restriction ρVUS is a distribution in D'(V) defined by
for all φ ∈ D(V).
Unless U = V, the restriction to V is neither injective nor surjective. Lack of surjectivity follows since distributions can blow up towards the boundary of V. For instance, if U = R and V = (0,2), then the distribution
is in D'(V) but admits no extension to D'(U).
Support of a distribution
Let S D′(U) be a distribution on an open set U. Then S is said to vanish on an open set V of U if S lies in the kernel of the restriction map ρVU. Explicitly S vanishes on V if
for all φ C∞(U) with support in V. Let V be a maximal open set on which the distribution S vanishes; i.e., V is the union of every open set on which S vanishes. The support of S is the complement of V in U. Thus
The distribution S has compact support if its support is a compact set. Explicitly, S has compact support if there is a compact subset K of U such that for every test function φ whose support is completely outside of K, we have S(φ) = 0. Compactly supported distributions define continuous linear functions on the space C∞(U); the topology on C∞(U) is defined such that φk converges to 0 if and only if all derivatives of φk converge uniformly to 0 on every compact subset of U. Conversely, it can be shown that every continuous linear functional on this space defines a distribution of compact support.
Tempered distributions and Fourier transform
By using a larger space of test functions, one can define the tempered distributions, a subspace of D'(Rn). These distributions are useful if one studies the Fourier transform in generality: all tempered distributions have a Fourier transform, but not all distributions have one.
The space of test functions employed here, the so-called Schwartz space S(Rn), is the space of all infinitely differentiable rapidly decreasing functions, where φ : Rn → R is called rapidly decreasing if any derivative of φ, multiplied with any power of |x|, converges towards 0 for |x| → ∞. These functions form a complete topological vector space with a suitably defined family of seminorms. More precisely, let
for α, β multi-indices of size n. Then φ is rapidly-decreasing if all the values
The family of seminorms pα, β defines a locally convex topology on the Schwartz-space. The seminorms are, in fact, norms on the Schwartz space, since Schwartz functions are smooth. The Schwartz space is metrizable and complete.
The space of tempered distributions is defined as the dual of the Schwartz space. In other words, a distribution F is a tempered distribution if and only if
for all multi-indices α, β implies
The derivative of a tempered distribution is again a tempered distribution. Tempered distributions generalize the bounded (or slow-growing) locally integrable functions; all distributions with compact support and all square-integrable functions are tempered distributions. All locally integrable functions f with at most polynomial growth, i.e. such that f(x)=O(|x|r) for some r, are tempered distributions. This includes all functions in Lp(Rn) for p≥1.
To study the Fourier transform, it is best to consider complex-valued test functions and complex-linear distributions. The ordinary continuous Fourier transform F yields then an automorphism of Schwartz-space, and we can define the Fourier transform of the tempered distribution S by (FS)(φ) = S(Fφ) for every test function φ. FS is thus again a tempered distribution. The Fourier transform is a continuous, linear, bijective operator from the space of tempered distributions to itself. This operation is compatible with differentiation in the sense that
and also with convolution: if S is a tempered distribution and ψ is a slowly increasing infinitely differentiable function on Rn (meaning that all derivatives of ψ grow at most as fast as polynomials), then Sψ is again a tempered distribution and
is the convolution of FS and Fψ.
Convolution
Under some circumstances, it is possible to define the convolution of a function with a distribution, or even the convolution of two distributions.
- Convolution of a test function with a distribution
If ƒ ∈ D(Rn) is a compactly supported smooth test function, then convolution with ƒ defines an operator
defined by Cƒg = ƒ*g, which is linear (and continuous with respect to the LF space topology on D(Rn).)
Convolution of ƒ with a distribution S ∈ D′(Rn) can be defined by taking the transpose of Cƒ relative to the duality pairing of D(Rn) with the space D′(Rn) of distributions (Trèves 1967, Chapter 27). If ƒ, g, φ ∈ D(Rn), then by Fubini's theorem
where 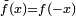 . Extending by continuity, the convolution of ƒ with a distribution S is defined by
. Extending by continuity, the convolution of ƒ with a distribution S is defined by
for all test functions φ ∈ D(Rn).
An alternative way to define the convolution of a function ƒ and a distribution S is to use the translation operator τx defined on test functions by
and extended by the transpose to distributions in the obvious way (Rudin 1991, §6.29). The convolution of the compactly supported function ƒ and the distribution S is then the function defined for each x ∈ Rn by
It can be shown that the convolution of a compactly supported function and a distribution is a smooth function. If the distribution S has compact support as well, then f*S is a compactly supported function, and the Titchmarsh convolution theorem (Hörmander 1983, Theorem 4.3.3) implies that
where ch denotes the convex hull.
- Distribution of compact support
It is also possible to define the convolution of two distributions S and T on Rn, provided one of them has compact support. Informally, in order to define S*T where T has compact support, the idea is to extend the definition of the convolution * to a linear operation on distributions so that the associativity formula
continues to hold for all test-functions φ. Hörmander (1983, §IV.2) proves the uniqueness of such an extension.
It is also possible to provide a more explicit characterization of the convolution of distributions (Tréves 1967, Chapter 27). Suppose that it is T that has compact support. For any test function φ in D(Rn), consider the function
It can be readily shown that this defines a smooth function of x, which moreover has compact support. The convolution of S and T is defined by
This generalizes the classical notion of convolution of functions and is compatible with differentiation in the following sense:
This definition of convolution remains valid under less restrictive assumptions about S and T; see for instance Gel'fand & Shilov (1966–1968, v. 1, pp. 103–104) and Benedetto (1997, Definition 2.5.8).
Distributions as derivatives of continuous functions
The formal definition of distributions exhibits them as a subspace of a very large space, namely the algebraic dual of D(U) (or S(Rd) for tempered distributions). It is not immediately clear from the definition how exotic a distribution might be. To answer this question, it is instructive to see distributions built up from a smaller space, namely the space of continuous functions. Roughly, any distribution is locally a (multiple) derivative of a continuous function. A precise version of this result, given below, holds for distributions of compact support, tempered distributions, and general distributions. Generally speaking, no proper subset of the space of distributions contains all continuous functions and is closed under differentiation. This says that distributions are not particularly exotic objects; they are only as complicated as necessary.
- Tempered distributions
If ƒ ∈ S′(Rn) is a tempered distribution, then there exists a constant C > 0, and positive integers M and N such that for all Schwartz functions φ ∈S(Rn)
This estimate along with some techniques from functional analysis can be used to show that there is a continuous slowly increasing function F and a multiindex α such that
- Compactly supported distributions
Let U be an open set, and K a compact subset of U. If ƒ is a distribution supported on K, then there is a continuous function F compactly supported in U (possibly on a larger set than K itself) such that
for some multi-index α. This follows from the previously quoted result on tempered distributions by means of a localization argument.
- Distributions with point support
If ƒ has support at a single point {P}, then ƒ is in fact a finite linear combination of distributional derivatives of the δ function at P. That is, there exists an integer m and complex constants aα for multi indices |α| ≤ m such that
where τP is the translation operator.
- General distributions
A version of the above theorem holds locally in the following sense (Rudin 1991). Let S be a distribution on U. Then for every multi-index α, there exists a continuous function gα such that any compact subset K of U intersects the supports of only finitely many gα, and such that
Using holomorphic functions as test functions
The success of the theory led to investigation of the idea of hyperfunction, in which spaces of holomorphic functions are used as test functions. A refined theory has been developed, in particular by Mikio Sato, using sheaf theory and several complex variables. This extends the range of symbolic methods that can be made into rigorous mathematics, for example Feynman integrals.
Problem of multiplication
A possible limitation of the theory of distributions (and hyperfunctions) is that it is a purely linear theory, in the sense that the product of two distributions cannot consistently be defined (in general), as has been proved by Laurent Schwartz in the 1950s. For example, if 1/x is the distribution obtained by extending the corresponding function to a homogeneous distribution, and δ is the Dirac delta distribution then
- (δ × x) × 1/x = 0
but
- δ × (x × 1/x) = δ
so the product of a distribution by a smooth function (which is always well defined) cannot be extended to an associative product on the space of distributions.
Thus, nonlinear problems cannot be posed in general and thus not solved within distribution theory alone. In the context of quantum field theory, however, solutions can be found. In more than two spacetime dimensions the problem is related to the regularization of "divergencies". Here Henri Epstein and Vladimir Glaser developed the mathematically rigorous (but extremely technical) causal perturbation theory. This does not solve the problem in other situations. Many other interesting theories are non linear, like for example Navier-Stokes equations of fluid dynamics.
In view of this, several not entirely satisfactory theories of algebras of generalized functions have been developed, among which Colombeau's (simplified) algebra is maybe the most popular in use today.
A simple solution of the multiplication problem is dictated by the path integral formulation of quantum mechanics. Since this is required to be equivalent to the Schrödinger theory of quantum mechanics which is invariant under coordinate transformations, this property must be shared by path integrals. This fixes all products of distributions as shown by Kleinert & Chervyakov (2001) The result is equivalent to what can be derived from dimensional regularization (Kleinert & Chervyakov 2000).
See also
- Generalized function
- Colombeau algebra
- Malgrange-Ehrenpreis theorem
- Pseudodifferential operator
- Riesz representation theorem
- Vague topology
- Weak solution
References
- Benedetto, J.J. (1997), Harmonic Analysis and Applications, CRC Press.
- Gel'fand, I.M.; Shilov, G.E. (1966–1968), Generalized functions, 1–5, Acadamic Press.
- Hörmander, L. (1983), The analysis of linear partial differential operators I, Grundl. Math. Wissenschaft., 256, Springer, MR0717035, ISBN 3-540-12104-8.
- Kleinert, H.; Chervyakov, A. (2001), "Rules for integrals over products of distributions from coordinate independence of path integrals", Europ. Phys. J. C 19: 743--747, doi:, http://www.physik.fu-berlin.de/~kleinert/kleiner_re303/wardepl.pdf.
- Kleinert, H.; Chervyakov, A. (2000), "Coordinate Independence of Quantum-Mechanical Path Integrals", Phys. Lett. A 269: 63, doi:, http://www.physik.fu-berlin.de/~kleinert/305/klch2.pdf.
- Rudin, W. (1991), Functional Analysis (2nd ed.), McGraw-Hill, ISBN 0-07-054236-8.
- Schwartz, L. (1954), "Sur l'impossibilité de la multiplications des distributions", C.R.Acad. Sci. Paris 239: 847-848.
- Schwartz, L. (1950–1951), Théorie des distributions, 1–2, Hermann.
- Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton University Press, ISBN 0-691-08078-X.
- Strichartz, R. (1994), A Guide to Distribution Theory and Fourier Transforms, CRC Press, ISBN 0849382734.
- Treves, François (1967), Topological Vector Spaces, Distributions and Kernels, Academic Press, pp. 126 ff.
Further reading
- M. J. Lighthill (1959). Introduction to Fourier Analysis and Generalised Functions. Cambridge University Press. ISBN 0-521-09128-4 (requires very little knowledge of analysis; defines distributions as limits of sequences of functions under integrals)
- H. Kleinert, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, World Scientific (Singapore, 2006)(also available online here). See Chapter 11 for defining products of distributions from the physical requirement of coordinate invariance.
- Vladimirov, V.S. (2001), "Generalized function", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104.
- Vladimirov, V.S. (2001), "Generalized functions, space of", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104.
- Vladimirov, V.S. (2001), "Generalized function, derivative of a", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104.
- Vladimirov, V.S. (2001), "Generalized functions, product of", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104.
- Oberguggenberger, Michael (2001), "Generalized function algebras", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104.