Neutrino
|
|
|
| Composition: | Elementary particle |
| Family: | Fermion |
| Group: | Lepton |
| Interaction: | weak interaction and gravitation |
| Antiparticle: | Antineutrino (possibly identical to the neutrino) |
| Theorized: | 1930 by Wolfgang Pauli |
| Discovered: | 1956 by Clyde Cowan, Frederick Reines, F. B. Harrison, H. W. Kruse, and A. D. McGuire. |
| Symbol(s): | νe, νμ, ντ |
| Types: | |
| Mass: | Nonzero, see Mass below |
| Electric charge: | 0 |
| Color charge: | 0 |
| Spin: | ½ |
Neutrinos are elementary particles that travel close to the speed of light, lack an electric charge, are able to pass through ordinary matter almost undisturbed and are thus extremely difficult to detect. Neutrinos have a minuscule, but nonzero mass. They are usually denoted by the Greek letter 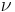 (nu).
(nu).
Neutrinos are created as a result of certain types of radioactive decay or nuclear reactions such as those that take place in the Sun, in nuclear reactors, or when cosmic rays hit atoms. There are three types, or "flavors", of neutrinos: electron neutrinos, muon neutrinos and tau neutrinos; each type also has an antimatter partner, called an antineutrino. Electron neutrinos or antineutrinos are generated whenever neutrons change into protons or vice versa, the two forms of beta decay. Interactions involving neutrinos are generally mediated by the weak force.
Most neutrinos passing through the Earth emanate from the sun, and more than 50 trillion solar electron neutrinos pass through the human body every second.[1]
Contents |
History

The neutrino was first postulated in 1930 by Wolfgang Pauli to preserve conservation of energy, conservation of momentum, and conservation of angular momentum in beta decay – the decay of a neutron into a proton, an electron and an antineutrino.[2] Pauli theorized that an undetected particle was carrying away the observed difference between the energy, momentum, and angular momentum of the initial and final particles.
The current name neutrino was coined by Enrico Fermi, who developed the first theory describing neutrino interactions, as a pun on neutrone, the Italian name of the neutron: neutrone seems to use the -one suffix (even though it is a complete word, not a compound), which in Italian indicates a large object, whereas -ino indicates a small one.
In 1942 Kan-Chang Wang first proposed to use beta-capture to experimentally detect neutrinos.[3] In 1956 Clyde Cowan, Frederick Reines, F. B. Harrison, H. W. Kruse, and A. D. McGuire published the article "Detection of the Free Neutrino: a Confirmation" in Science, a result that was rewarded with the 1995 Nobel Prize. In this experiment, now known as the neutrino experiment, neutrinos created in a nuclear reactor by beta decay were shot into protons producing neutrons and positrons both of which could be detected. It is now known that both the proposed and the observed particles were antineutrinos.
In 1962 Leon M. Lederman, Melvin Schwartz and Jack Steinberger showed that more than one type of neutrino exists by first detecting interactions of the muon neutrino (already hypothesised with the name neutretto[4]), which earned them the 1988 Nobel Prize. When a third type of lepton, the tau, was discovered in 1975 at the Stanford Linear Accelerator, it too was expected to have an associated neutrino. First evidence for this third neutrino type came from the observation of missing energy and momentum in tau decays analogous to the beta decay leading to the discovery of the neutrino. The first detection of tau neutrino interactions was announced in summer of 2000 by the DONUT collaboration at Fermilab, making it the latest particle of the Standard Model to have been directly observed; its existence had already been inferred by both theoretical consistency and experimental data from LEP.
Starting in the late 1960s, several experiments found that the number of electron neutrinos arriving from the sun was between one third and one half the number predicted by the Standard Solar Model, a discrepancy which became known as the solar neutrino problem and remained unresolved for some thirty years.
The Standard Model of particle physics assumes massless neutrinos that don't change flavor. However, nonzero neutrino mass and accompanying flavor oscillation remained a possibility.
A practical method for investigating neutrino masses (that is, flavor oscillation) was first suggested by Bruno Pontecorvo in 1957 using an analogy with the neutral kaon system; over the subsequent 10 years he developed the mathematical formalism and the modern formulation of vacuum oscillations. In 1985 Stanislav Mikheyev and Alexei Smirnov (expanding on 1978 work by Lincoln Wolfenstein) noted that flavor oscillations can be modified when neutrinos propagate through matter. This so-called MSW effect is important to understand neutrinos emitted by the Sun, which pass through its dense atmosphere on their way to detectors on Earth.
Starting in 1998, experiments began to show that solar and atmospheric neutrinos change flavors (see Super-Kamiokande, Sudbury Neutrino Observatory). This resolved the solar neutrino problem: the electron neutrinos produced in the sun had partly changed into other flavors which the experiments could not detect.
Although individual experiments, such as the set of solar neutrino experiments, are consistent with non-oscillatory mechanisms of neutrino flavor conversion, taken altogether, neutrino experiments imply the existence of neutrino oscillations. Especially relevant in this context are the reactor experiment KamLAND and the accelerator experiments such as MINOS. The KamLAND experiment has indeed identified oscillations as the neutrino flavor conversion mechanism involved in the solar electron neutrinos. Similarly MINOS confirms the oscillation of atmospheric neutrinos and gives a better determination of the mass squared splitting.[5]
Raymond Davis Jr. and Masatoshi Koshiba were jointly awarded the 2002 Nobel Prize in Physics. Ray Davis for his pioneer work on cosmic neutrinos and Koshiba for the first real time observation of supernova neutrinos. The detection of solar neutrinos, and of neutrinos of SN 1987A supernova in 1987 marked the beginning of neutrino astronomy.
Properties
The neutrino has half-integer spin (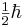 ) and is therefore a fermion. Neutrinos interact primarily through the weak force. The discovery of neutrino flavor oscillations implies that neutrinos are massive. The existence of a neutrino mass strongly suggests the existence of a tiny neutrino magnetic moment[6] of the order of
) and is therefore a fermion. Neutrinos interact primarily through the weak force. The discovery of neutrino flavor oscillations implies that neutrinos are massive. The existence of a neutrino mass strongly suggests the existence of a tiny neutrino magnetic moment[6] of the order of 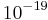 Bohr magneton allowing the possibility that neutrinos may interact electromagnetically as well.
Bohr magneton allowing the possibility that neutrinos may interact electromagnetically as well.
An experiment done by C. S. Wu at Columbia University showed that neutrinos always have left-handed chirality.
It is very hard to uniquely identify neutrino interactions among the natural background of radioactivity. For this reason, in early experiments a special reaction channel was chosen to facilitate the identification: the interaction of an antineutrino with one of the hydrogen nuclei in the water molecules. A hydrogen nucleus is a single proton, so simultanous nuclear interactions within an heavier nucleus don't need to be considered for the detection experiment. Within a cubic metre of water placed right outside a nuclear reactor, only relatively few such interactions can be recorded, but the setup is nowadays evaluated for measuring the reactor's plutonium production rate.
It should be noted that neutrinos traveling through matter, in general, undergo a process analogous to light traveling through a transparent material. This process is not directly observable because it isn't (and doesn't produce) ionizing radiation, but gives rise to the MSW effect. Only a small fraction of the neutrino's energy is transferred to the target material.
Neutrinos can interact with a more heavy nucleus changing it to another nucleus. This process is used in radiochemical neutrino detectors. In this case, the energy levels and spin states within the target nucleus have to be taken into account to estimate the probability for an interaction. In general the interaction probability increases with the number of neutrons and protons within a nucleus.
Types of neutrinos
| Fermion | Symbol | Mass[7] |
|---|---|---|
| Generation 1 (electron) | ||
| Electron neutrino | 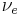 |
< 2.2 eV |
| Electron antineutrino | 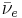 |
< 2.2 eV |
| Generation 2 (muon) | ||
| Muon neutrino | 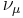 |
< 170 keV |
| Muon antineutrino | 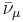 |
< 170 keV |
| Generation 3 (tau) | ||
| Tau neutrino | 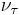 |
< 15.5 MeV |
| Tau antineutrino | 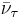 |
< 15.5 MeV |
There are three known types (flavors) of neutrinos: electron neutrino νe, muon neutrino νμ and tau neutrino ντ, named after their partner leptons in the Standard Model (see table at right). The current best measurement of the number of neutrino types comes from observing the decay of the Z boson. This particle can decay into any light neutrino and its antineutrino, and the more types of light neutrinos available, the shorter the lifetime of the Z boson. Measurements of the Z lifetime have shown that the number of light neutrino types (with "light" meaning of less than half the Z mass) is 3.[6] The correspondence between the six quarks in the Standard Model and the six leptons, among them the three neutrinos, suggests to physicists' intuition that there should be exactly three types of neutrino. However, actual proof that there are only three kinds of neutrinos remains an elusive goal of particle physics.
The possibility of sterile neutrinos — relatively light neutrinos which do not participate in the weak interaction but which could be created through flavor oscillation (see below) — is unaffected by these Z-boson-based measurements, and the existence of such particles is in fact hinted by experimental data from the LSND experiment. However, the currently running MiniBooNE experiment suggested, until recently, that sterile neutrinos are not required to explain the experimental data,[8] although the latest research into this area is on-going and anomalies in the MiniBooNE data may allow for exotic neutrino types, including sterile neutrinos.[9]
Flavor oscillations
Neutrinos are most often created or detected with a well defined flavor (electron, muon, tau). However, in a phenomenon known as neutrino flavor oscillation, neutrinos are able to oscillate between the three available flavors while they propagate through space. Specifically, this occurs because the neutrino flavor eigenstates are not the same as the neutrino mass eigenstates (simply called 1, 2, 3). This allows for a neutrino that was produced as an electron neutrino at a given location to have a calculable probability to be detected as either a muon or tau neutrino after it has traveled to another location. This quantum mechanical effect was first hinted by the discrepancy between the number of electron neutrinos detected from the Sun's core failing to match the expected numbers, dubbed as the "solar neutrino problem." In the Standard Model the existence of flavor oscillations implies a nonzero neutrino mass, because the amount of mixing between neutrino flavors at a given time depends on the differences in their squared-masses.
It is possible that the neutrino and antineutrino are in fact the same particle, a hypothesis first proposed by the Italian physicist Ettore Majorana. The neutrino could transform into an antineutrino (and vice versa) by flipping the orientation of its spin state.
This change in spin would require the neutrino and antineutrino to have nonzero mass, and therefore travel slower than light, because such a spin flip caused only by a change in point of view, can take place only if inertial frames of reference exist that move faster than the particle: such a particle has a spin of one orientation when seen from a frame which moves slower than the particle, but the opposite spin when observed from a frame that moves faster than the particle.
Speed
Before the idea of neutrino oscillations came up, it was generally assumed that neutrinos travel at the speed of light. The question of neutrino velocity is closely related to their mass. According to relativity, if neutrinos are massless, they must travel at the speed of light. However, if they carry a mass, they cannot reach the speed of light.
In the early 1980s, first measurements of neutrino speed were done using pulsed pion beams (produced by pulsed proton beams hitting a target). The pions decayed producing neutrinos, and the neutrino interactions observed within a time window in a detector at a distance were consistent with the speed of light. This measurement has been repeated using the MINOS detectors, which found the speed of 3 GeV neutrinos to be (1 − (5.1 ± 2.9)×10−5) times the speed of light. While the central value is lower than the speed of light, the uncertainty is great enough that it is very likely that the true velocity is too close to the speed of light to see the difference. This measurement set an upper bound on the mass of the muon neutrino of 50 MeV at 99% confidence.[10]
The same observation was made, on a somewhat larger scale, with supernova 1987a. The neutrinos from the supernova were detected within a time window that was consistent with a speed of light for the neutrinos. So far, the question of neutrino masses cannot be decided based on measurements of the neutrino speed.
Mass
The Standard Model of particle physics assumes that neutrinos are massless, although adding massive neutrinos to the basic framework is not difficult. Indeed, the experimentally established phenomenon of neutrino oscillation requires neutrinos to have nonzero masses.[8]
The strongest upper limit on the masses of neutrinos comes from cosmology: the Big Bang model predicts that there is a fixed ratio between the number of neutrinos and the number of photons in the cosmic microwave background. If the total energy of all three types of neutrinos exceeded an average of 50 electronvolts per neutrino, there would be so much mass in the universe that it would collapse. This limit can be circumvented by assuming that the neutrino is unstable; however, there are limits within the Standard Model that make this difficult. A much more stringent constraint comes from a careful analysis of cosmological data, such as the cosmic microwave background radiation, galaxy surveys and the Lyman-alpha forest. These indicate that the sum of the neutrino masses must be less than 0.3 electronvolt.[11]
In 1998, research results at the Super-Kamiokande neutrino detector determined that neutrinos do indeed flavor oscillate, and therefore have mass. While this shows that neutrinos have mass, the absolute neutrino mass scale is still not known. This is due to the fact that neutrino oscillations are sensitive only to the difference in the squares of the masses.[12]
The best estimate of the difference in the squares of the masses of mass eigenstates 1 and 2 was published by KamLAND in 2005: Δm212 = 0.000079 eV2.[13] In 2006, the MINOS experiment measured oscillations from an intense muon neutrino beam, determining the difference in the squares of the masses between neutrino mass eigenstates 2 and 3. The initial results indicate |Δm322| = 0.0027 eV2, consistent with previous results from Super-K.[14] Since |Δm322| is the difference of two squared masses, at least one of them has to have a value which is at least the square root of this value. Thus, there exists at least one neutrino mass eigenstate with a mass of at least 0.04 eV.[15]
Currently a number of efforts are under way to directly determine the absolute neutrino mass scale in laboratory experiments. The methods applied involve nuclear beta decay (KATRIN and MARE) or neutrinoless double beta decay (e.g. GERDA, CUORE/Cuoricino, NEMO 3 and others).
Handedness
Experimental results show that (nearly) all produced and observed neutrinos have left-handed helicities (spins antiparallel to momenta), and all antineutrinos have right-handed helicities, within the margin of error. In the massless limit, it means that only one of two possible chiralities is observed for either particle. These are the only chiralities included in the Standard Model of particle interactions.
It is possible that their counterparts (right-handed neutrinos and left-handed antineutrinos) simply do not exist. If they do, their properties are substantially different from observable neutrinos and antineutrinos. It is theorized that they are either very heavy (on the order of GUT scale—see Seesaw mechanism), do not participate in weak interaction (so-called sterile neutrinos), or both.
The existence of nonzero neutrino masses somewhat complicates the situation. Neutrinos are produced in weak interactions as chirality eigenstates. However, chirality of a massive particle is not a constant of motion; helicity is, but the chirality operator does not share eigenstates with the helicity operator. Free neutrinos propagate as mixtures of left- and right-handed helicity states, with mixing amplitudes on the order of 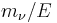 . This does not significantly affect the experiments, because neutrinos involved are nearly always ultrarelativistic, and thus mixing amplitudes are vanishingly small (for example, most solar neutrinos have energies on the order of 100 keV–1 MeV, so the fraction of neutrinos with "wrong" helicity among them cannot exceed 10-10).[16][17]
. This does not significantly affect the experiments, because neutrinos involved are nearly always ultrarelativistic, and thus mixing amplitudes are vanishingly small (for example, most solar neutrinos have energies on the order of 100 keV–1 MeV, so the fraction of neutrinos with "wrong" helicity among them cannot exceed 10-10).[16][17]
Neutrino sources
Artificially produced neutrinos
Nuclear reactors are the major source of human-generated neutrinos. Anti-neutrinos are made in the beta-decay of neutron-rich daughter fragments in the fission process. Generally, the four main isotopes contributing to the anti-neutrino flux are: uranium-235, uranium-238, plutonium-239, plutonium-241 (e.g. the anti-neutrinos emitted during beta-minus decay of their respective fission fragments). The average nuclear fission releases about 200 MeV of energy, of which roughly 6% (or 9 MeV, depending on quoted reference) are radiated away as anti-neutrinos. For a typical nuclear reactor with a thermal power of 4,000 MW (megawatts) and an electrical power generation of 1,300 MW, this corresponds to a total power production of 4,250 MW, of which 250 MW is radiated away as anti-neutrino radiation. This is to say, 250 MW of fission energy is lost from this reactor and does not appear as heat, since the anti-neutrinos penetrate all normal building materials essentially tracelessly. The energy spectrum depends, for example, on the degree to which the fuel is burned.
There is no established experimental method to measure the flux of low energy anti-neutrinos. Only anti-neutrinos with an energy above threshold of 1.8 MeV can be uniquely identified (see neutrino detection below). An estimated 3% of all anti-neutrinos from a nuclear reactor carry an energy above this threshold. An average nuclear power plant may generate over 1020 anti-neutrinos per second above this threshold, and a much larger number which cannot be seen with present detector technology.
Some particle accelerators have been used to make neutrino beams. The technique is to smash protons into a fixed target, producing charged pions or kaons. These unstable particles are then magnetically focused into a long tunnel where they decay while in flight. Because of the relativistic boost of the decaying particle the neutrinos are produced as a beam rather than isotropically. Efforts to construct an accelerator facility where neutrinos are produced through muon decays are ongoing.[18] Such a setup is generally known as a neutrino factory.
Nuclear bombs also produce very large quantities of neutrinos. Fred Reines and Clyde Cowan considered the detection of neutrinos from a bomb prior to their search for reactor neutrinos.
Geologically produced neutrinos
Neutrinos are produced as a result of natural background radiation. In particular, the decay chains of uranium-238 and thorium-232 isotopes, as well as potassium-40, include beta decays which emit anti-neutrinos. These so-called geoneutrinos can provide valuable information on the Earth's interior. A first indication for geoneutrinos was found by the KamLAND experiment in 2005. KamLAND's main background in the geoneutrino measurement are the anti-neutrinos coming from reactors. Several future experiments aim at improving the geoneutrino measurement and these will necessarily have to be far away from reactors.

Atmospheric neutrinos
Atmospheric neutrinos result from the interaction of cosmic rays with atomic nuclei in the Earth's atmosphere, creating showers of particles, many of which are unstable and produce neutrinos when they decay. A collaboration of particle physicists from Tata Institute of Fundamental Research (TIFR), India, Osaka City University, Japan and Durham University, UK recorded the first cosmic ray neutrino interaction in an underground laboratory in KGF gold mines in India in 1965.
Solar neutrinos
Solar neutrinos originate from the nuclear fusion powering the sun and other stars. The details of the operation of the sun are explained by the Standard Solar Model. In short: when four protons fuse to become one helium nucleus, two of them have to convert into neutrons, and each such conversion releases one electron neutrino.
The sun sends enormous numbers of neutrinos in all directions. Every second, about 65 billion (6.5×1010) solar neutrinos pass through every square centimeter on Earth that faces the sun.[19] Since neutrinos are insignificantly absorbed by the mass of the Earth, the surface area on the side of the Earth opposite the Sun receives about the same number of neutrinos as the side facing the Sun.
Supernovae

Neutrinos are an important product of Types Ib, Ic and II (core-collapse) supernovae. In such events, the pressure at the core becomes so high (1014 g/cm³) that the degeneracy of electrons is not enough to prevent protons and electrons from combining to form a neutron and an electron neutrino. A second and more important neutrino source is the thermal energy (100 billion kelvins) of the newly formed neutron core, which is dissipated via the formation of neutrino-antineutrino pairs of all flavors.[20] Most of the energy produced in supernovas is thus radiated away in the form of an immense burst of neutrinos. The first experimental evidence of this phenomenon came in 1987, when neutrinos from supernova 1987A were detected. The water-based detectors Kamiokande II and IMB detected 11 and 8 antineutrinos of thermal origin,[20] respectively, while the gallium-71-based Baksan detector found 5 neutrinos (lepton number = 1) of either thermal or electron-capture origin, in a burst lasting less than 13 seconds. It is thought that neutrinos would also be produced from other events such as the collision of neutron stars. What was particularly interesting about this event was that the neutrino signature of the supernova arrived at earth approximately 18 hours before the arrival of the first photon signature (Warning: compare with SNEWS where the delay is stated as being 3 hours!). The exceptionally weak interaction with normal matter allowed the neutrinos to pass through the churning mass of the exploding star, while the electromagnetic photons were retarded, with the photon signature of the supernova not being released until the outermost layers of the star were superheated and released a much brighter visible light signature, observed telescopically on earth some 18 hours after the neutrinos had already arrived. This shows how weakly interacting neutrinos truly are.
Because neutrinos interact so little with matter, it is thought that a supernova's neutrino emissions carry information about the innermost regions of the explosion. Much of the visible light comes from the decay of radioactive elements produced by the supernova shock wave, and even light from the explosion itself is scattered by dense and turbulent gases. Neutrinos, on the other hand, pass through these gases, providing information about the supernova core (where the densities were large enough to influence the neutrino signal). Furthermore, the neutrino burst is expected to reach Earth before any electromagnetic waves, including visible light, gamma rays or radio waves. The exact time delay is unknown, but for a Type II supernova, astronomers expect the neutrino flood to be released seconds after the stellar core collapse, while the first electromagnetic signal may be hours or days later. The SNEWS project uses a network of neutrino detectors to monitor the sky for candidate supernova events; it is hoped that the neutrino signal will provide a useful advance warning of an exploding star.
The energy of supernova neutrinos ranges from a few to several tens of MeV. However, the sites where cosmic rays are accelerated are expected to produce neutrinos that are one million times more energetic or more, produced from turbulent gasesous environments left over by supernova explosions: the supernova remnants. The connection between cosmic rays and supernova remnants was suggested by Walter Baade and Fritz Zwicky, shown to be consistent with the cosmic ray losses of the Milky Way if the efficiency of acceleration is about 10 percent by Ginzburg and Syrovatsky, and it is supported by a specific mechanism called "shock wave acceleration" based on Fermi ideas (which is still under development). The very high energy neutrinos are still to be seen, but this branch of neutrino astronomy is just in its infancy. The main existing or forthcoming experiments that aim at observing very high energy neutrinos from our galaxy are Baikal, AMANDA, IceCube, Antares, NEMO and Nestor. Related information is provided by very high energy gamma ray observatories, such as HESS and MAGIC. Indeed, the collisions of cosmic rays are supposed to produce charged pions, whose decay give the neutrinos, but also neutral pions, whose decay give gamma rays: the environment of a supernova remnant is transparent to both types of radiation.
Still higher energy neutrinos, resulting from the interactions of extragalactic cosmic rays, could be observed with the Pierre Auger Observatory or with the dedicated experiment named ANITA.
Cosmic background radiation
It is thought that, just like the cosmic microwave background radiation left over from the Big Bang, there is a background of low energy neutrinos in our Universe. In the 1980s it was proposed that these may be the explanation for the dark matter thought to exist in the universe. Neutrinos have one important advantage over most other dark matter candidates: we know they exist. However, they also have serious problems.
From particle experiments, it is known that neutrinos are very light. This means that they move at speeds close to the speed of light except when they have extremely low kinetic energy. Thus, dark matter made from neutrinos is termed "hot dark matter". The problem is that being fast moving, the neutrinos would tend to have spread out evenly in the universe before cosmological expansion made them cold enough to congregate in clumps. This would cause the part of dark matter made of neutrinos to be smeared out and unable to cause the large galactic structures that we see.
Further, these same galaxies and groups of galaxies appear to be surrounded by dark matter which is not fast enough to escape from those galaxies. Presumably this matter provided the gravitational nucleus for formation. This implies that neutrinos make up only a small part of the total amount of dark matter.
From cosmological arguments, relic background neutrinos are estimated to have density of 56 of each type per cubic centimeter and temperature 1.9 K (1.7×10-4 eV) if they are massless, much colder if their mass exceeds 0.001 eV. Although their density is quite high, due to extremely low neutrino cross-sections at sub-eV energies, the relic neutrino background has not yet been observed in the laboratory. In contrast, boron-8 solar neutrinos — which are emitted with a higher energy — have been detected definitively despite having a space density that is lower than that of relic neutrinos by some 6 orders of magnitude.
Neutrino detection
Because neutrinos are very weakly interacting, neutrino detectors must be very large in order to detect a significant number of neutrinos. Neutrino detectors are often built underground in order to isolate the detector from cosmic rays and other background radiation.
Antineutrinos were first detected in the 1950s near a nuclear reactor. Reines and Cowan used two targets containing a solution of cadmium chloride in water. Two scintillation detectors were placed next to the cadmium targets. Antineutrino with an energy above the threshold of 1.8 MeV caused charged current interactions with the protons in the water, producing positrons and neutrons. The resulting positron annihilations with electrons created photons with an energy of about 0.5 MeV. Pairs of photons in coincidence could be detected by the two scintillation detectors above and below the target. The neutrons were captured by cadmium nuclei resulting in gamma rays of about 8 MeV that were detected a few microseconds after the photons from a positron annihilation event.
Since then, various detection methods have been used. Super Kamiokande is a large volume of water surrounded by photomultiplier tubes that watch for the Cherenkov radiation emitted when an incoming neutrino creates an electron or muon in the water. The Sudbury Neutrino Observatory is similar, but uses heavy water as the detecting medium, which uses the same effects, but also allows the additional reaction any-flavor neutrino photo-dissociation of deuterium, resulting in a free neutron which is then detected from gamma radiation after chlorine-capture. Other detectors have consisted of large volumes of chlorine or gallium which are periodically checked for excesses of argon or germanium, respectively, which are created by electron-neutrinos interacting with the original substance. MINOS uses a solid plastic scintillator coupled to photomultiplier tubes, while Borexino uses a liquid pseudocumene scintillator also watched by photomultiplier tubes while the proposed NOνA detector will use liquid scintillator watched by avalanche photodiodes.
Motivation for scientific interest in the neutrino
The neutrino is of scientific interest because it can make an exceptional probe for environments that are typically concealed from the standpoint of other observation techniques, such as optical and radio observation.
The first such use of neutrinos was proposed in the early 20th century for observation of the core of the Sun. Direct optical observation of the solar core is impossible due to the diffusion of electromagnetic radiation by the huge amount of matter surrounding the core. On the other hand, neutrinos generated in stellar fusion reactions interact very weakly with matter, and pass through the sun with few interactions. While photons emitted by the solar core may require some 40,000 years to diffuse to the outer layers of the Sun, neutrinos are virtually unimpeded and cross this distance at nearly the speed of light.[21][22]
Neutrinos are also useful for probing astrophysical sources beyond our solar system. Neutrinos are the only known particles that are not significantly attenuated by their travel through the interstellar medium. Optical photons can be obscured or diffused by dust, gas and background radiation. High-energy cosmic rays, in the form of fast-moving protons and atomic nuclei, are not able to travel more than about 100 megaparsecs due to the GZK cutoff. Neutrinos can travel this and greater distances with very little attenuation.
The galactic core of the Milky Way is completely obscured by dense gas and numerous bright objects. However, it is likely that neutrinos produced in the galactic core will be measurable by Earth-based neutrino telescopes in the next decade.
Another important use of the neutrino is in the observation of supernovae, the explosions that end the lives of highly massive stars. The core collapse phase of a supernova is an almost unimaginably dense and energetic event. It is so dense that no known particles are able to escape the advancing core front except for neutrinos. Consequently, supernovae are known to release approximately 99% of their energy in a rapid (10 second) burst of neutrinos. As a result, the usefulness of neutrinos as a probe for this important event in the death of a star cannot be overstated.
Determining the mass of the neutrino (see above) is also an important test of cosmology (see Dark matter). Many other important uses of the neutrino may be imagined in the future. It is clear that the astrophysical significance of the neutrino as an observational technique is comparable with all other known techniques, and is therefore a major focus of study in astrophysical communities.
In particle physics the main virtue of studying neutrinos is that they are typically the lowest mass, and hence lowest energy examples of particles theorized in extensions of the Standard Model of particle physics. For example, one would expect that if there is a fourth class of fermions beyond the electron, muon, and tau generations of particles, that a fourth generation neutrino would be the easiest to generate in a particle accelerator.
Neutrinos could also be used for studying quantum gravity effects. Because they are not affected by either the strong interaction or electromagnetism, and because they are not normally found in composite particles (unlike quarks) or prone to near instantaneous decay (like many other standard model particles) it might be possible to isolate and measure gravitational effects on neutrinos at a quantum level.
See also
- List of neutrino experiments
- Neutrino factory
Notes
- ↑ MIT News Office, "Experiment confirms famous physics model" April 18, 2007
- ↑ K. Riesselmann (2007). "Logbook: Neutrino Invention". Symmetry 4 (2). http://www.symmetrymagazine.org/cms/?pid=1000450.
- ↑ Wang, Kan Chang (January 1942). "A Suggestion on the Detection of the Neutrino". Physical Review 61 (1-2): 97. doi:. http://prola.aps.org/abstract/PR/v61/i1-2/p97_1.
- ↑ Ivan V. Anicin (2005). "The Neutrino - Its Past, Present and Future". arΧiv: physics/0503172v1 [physics] Retrieved on 2008-06-09.
- ↑ M. Maltoni et al. (2004). "Status of global fits to neutrino oscillations". NJP 06: 122. doi:. arΧiv:hep-ph/0405172
- ↑ 6.0 6.1 Particle Data Group (S. Eidelman et al.) (2004). "Leptons in the 2005 Review of Particle Physics". Phys. Lett. B 592 (1): 1–5. http://pdg.lbl.gov/2005/listings/lxxx.html. Retrieved on 2007-11-25.
- ↑ Since neutrino flavor eigenstates are not the same as neutrino mass eigenstates (see neutrino oscillation), the given masses are actually mass expectation values. If the mass of a neutrino could be measured directly, the value would always be that of one of the three mass eigenstates: ν1, ν2, and ν3. In practice, the mass cannot be measured directly. Instead it is measured by looking at the shape of the endpoint of the energy spectrum in particle decays. This sort of measurement directly measures the expectation value of the mass; it is not sensitive to any of the mass eigenstates separately.
- ↑ 8.0 8.1 Karagiorgi, G.; A. Aguilar-Arevalo, J. M. Conrad, and M. H. Shaevitz (2007). "Leptonic CP violation studies at MiniBooNE in the (3+2) sterile neutrino oscillation hypothesis". Phys Rev D 75 (013011): 1–8. doi:. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=PRVDAQ000075000001013011000001&idtype=cvips&gifs=yes.
- ↑ Alpert, M. (August 2007). "Dimensional Shortcuts". Scientific American. http://www.sciam.com/article.cfm?chanID=sa006&colID=5&articleID=B5CB9C67-E7F2-99DF-3BF7368614D46C5D.
- ↑ Measurement of neutrino velocity with the MINOS detectors and NuMI neutrino beam, Adamson et al., arΧiv:hep-ex/0706.0437
- ↑ Goobar, Ariel; Steen Hannestad, Edvard Mortsell, Huitzu Tu (June 2006). "The neutrino mass bound from WMAP 3 year data, the baryon acoustic peak, the SNLS supernovae and the Lyman-α forest". Journal of Cosmology and Astroparticle Physics 606 (19). doi:.
- ↑ R. N. Mohapatra et al. (APS neutrino theory working group) (2005). "Theory of neutrinos: a white paper". Preprint. arΧiv:hep-ph/0510213
- ↑ KamLAND Collaboration, Phys. Rev. Lett.&mbsp;94 (2005) 081801
- ↑ "MINOS experiment sheds light on mystery of neutrino disappearance". Fermilab (30 March 2006). Retrieved on 2007-11-25.
- ↑ C. Amsler et al. (PDG) (2008). "The Review of Particle Physics". Physics Letters B667, 1 (2008)., see especially chapter 13 Neutrino Mass, Mixing, and Flavor Change
- ↑ B. Kayser (2005). "Neutrino mass, mixing, and flavor change" (PDF). Particle Data Group. Retrieved on 2007-11-25.
- ↑ Bilenky, S.M.; Giunti, C. (2001). "Lepton Numbers in the framework of Neutrino Mixing". Int. J. Mod. Phys. A 16 (3931). http://www.nu.to.infn.it/pap/0102320/. Retrieved on 2007-11-25.
- ↑ Bandyopadhyay, A. et al. (ISS Physics Working Group) (2007). "Physics at a future Neutrino Factory and super-beam facility". Preprint. arΧiv:0710.4947
- ↑ Bellerive, A (March 2004). "Review of Solar Neutrino Experiments". International Journal of Modern Physics A 19 (8): 1167–1179. doi:. http://www.worldscinet.com/cgi-bin/details.cgi?id=pii:S0217751X04019093&type=html.
- ↑ 20.0 20.1 Mann, Alfred K. (1997). Shadow of a star: The neutrino story of Supernova 1987A. New York: W. H. Freeman. pp. 122. ISBN 0716730979. http://www.whfreeman.com/GeneralReaders/book.asp?disc=TRAD&id_product=1058001008&@id_course=1058000240.
- ↑ J.N. Bahcall, Neutrino Astrophysics, Cambridge, 1989.
- ↑ Davis, Raymond, Jr. (July 2003). "Nobel Lecture: A half-century with solar neutrinos". Reviews of Modern Physics 75 (3): 10. doi:. http://prola.aps.org/abstract/RMP/v75/i3/p985_1.
References
- G. A. Tammann, F. K. Thielemann, D. Trautmann (2003). "Opening new windows in observing the Universe". Europhysics News. Retrieved on 2006-06-08.
- Bahcall, John N. (1989). Neutrino Astrophysics. Cambridge University Press. ISBN 0-521-35113-8.
- Griffiths, David J. (1987). Introduction to Elementary Particles. Wiley, John & Sons, Inc. ISBN 0-471-60386-4.
- Perkins, Donald H. (1999). Introduction to High Energy Physics. Cambridge University Press. ISBN 0-521-62196-8.
- Povh, Bogdan (1995). Particles and Nuclei: An Introduction to the Physical Concepts. Springer-Verlag. ISBN 0-387-59439-6.
- Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman. ISBN 0-7167-4345-0.
- Neutrino Oscillations, Masses And Mixing: W.M.Alberico, Torino University&S.M. Bilenky, Dubna NRI; 2003;http://arxiv.org/abs/hep-ph/0306239v1
External links
- NEUTRINO UNBOUND: On-line review and e-archive on Neutrino Physics and Astrophysics
- Nova: The Ghost Particle: Documentary on US public television from WGBH
- SNEWS: Using neutrino detectors to receive early warning of supernovae
- Measuring the density of the earth's core with neutrinos
- John Bahcall Website
- Universe submerged in a sea of chilled neutrinos, New Scientist, 5 March 2008
|
||||||||||||||||||||