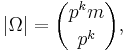Sylow theorems

In mathematics, specifically group theory, the Sylow theorems, named after Ludwig Sylow, form a partial converse to Lagrange's theorem, which states that if H is a subgroup of a finite group G, then the order of H divides the order of G. The Sylow theorems guarantee, for certain divisors of the order of G, the existence of corresponding subgroups, and give information about the number of those subgroups.

Contents

Definition

Let p be a prime number; then we define a Sylow p-subgroup (sometimes p-Sylow subgroup) of G to be a maximal p-subgroup of G (i.e., a subgroup which is a p-group, and which is not a proper subgroup of any other p-subgroup of G). The set of all Sylow p-subgroups for a given prime p is sometimes written Sylp(G).

Collections of subgroups which are each maximal in one sense or another are not uncommon in group theory. The surprising result here (see below) is that in the case of Sylp(G), all members are actually isomorphic to each other and have the largest possible order: if |G| = pns where p does not divide s, then any Sylow p-subgroup P has order |P| = pn. That is, P is a p-group and gcd(|G:P|, p) = 1. These properties can be exploited to further analyze the structure of G.

Sylow theorems

The following theorems were first proposed and proven by Norwegian mathematician Ludwig Sylow in 1872, and published in Mathematische Annalen. Given a finite group G and a prime p which divides the order of G, we can write the order of G as pn · s, where n > 0 and p does not divide s.

Theorem 1: There exists a Sylow p-subgroup of G, of order pn.

The following weaker version of theorem 1 was first proved by Cauchy.

Corollary: Given a finite group G and a prime number p dividing the order of G, then there exists an element of order p in G .

Theorem 2: All Sylow p-subgroups of G are conjugate (and therefore isomorphic) to each other, i.e. if H and K are Sylow p-subgroups of G, then there exists an element g in G with g−1Hg = K.

Theorem 3: Let np be the number of Sylow p-subgroups of G.

In particular, the above implies that every Sylow p-subgroup is of the same order, pn; conversely, if a subgroup has order pn, then it is a Sylow p-subgroup, and so is isomorphic to every other Sylow p-subgroup. Due to the maximality condition, if H is any p-subgroup of G, then H is a subgroup of a p-subgroup of order pn.

A very important consequence of Theorem 3 is that the condition np = 1 is equivalent to saying that the Sylow p-subgroup of G is a normal subgroup. (There are groups which have normal subgroups but no normal Sylow subgroups, such as S4.)

There is an analogue of the Sylow theorems for infinite groups. We define a Sylow p-subgroup in an infinite group to be a p-subgroup (that is, every element in it has p-power order) which is maximal for inclusion among all p-subgroups in the group. Such subgroups exist by Zorn's lemma.

Theorem: If K is a Sylow p-subgroup of G, and np = |Cl(K)| is finite, then every Sylow p-subgroup is conjugate to K, and np = 1 mod p, where Cl(K) denotes the conjugacy class of K.

Example applications

Let G be a group of order 15 = 3 · 5. We have that n3 must divide 5, and n3 = 1 mod 3. The only value satisfying these constraints is 1; therefore, there is only one subgroup of order 3, and it must be normal (since it has no distinct conjugates). Similarly, n5 divides 3, and n5 = 1 mod 5; thus it also has a single normal subgroup of order 5. Since 3 and 5 are coprime, the intersection of these two subgroups is trivial, and so G must be the direct product of groups of order 3 and 5, that is the cyclic group of order 15. Thus, there is only one group of order 15 (up to isomorphism).

A more complex example involves the order of the smallest simple group which isn't cyclic. Burnside's paqb theorem states that if the order of a group is the product of two prime powers, then it is solvable, and so the group is not simple, or is of prime order and is cyclic. This rules out every group up to order 30 ( = 2 · 3 · 5).

If G is simple, and |G| = 30, then n3 must divide 10 ( = 2 · 5), and n3 = 1 mod 3. Therefore n3 = 10, since neither 4 nor 7 divides 10, and if n3 = 1 then, as above, G would have a normal subgroup of order 3, and could not be simple. G then has 10 distinct cyclic subgroups of order 3, each of which has 2 elements of order 3 (plus the identity). This means G has at least 20 distinct elements of order 3. As well, n5 = 6, since n5 must divide 6 ( = 2 · 3), and n5 = 1 mod 5. So G also has 24 distinct elements of order 5. But the order of G is only 30, so a simple group of order 30 cannot exist.

Next, suppose |G| = 42 = 2 · 3 · 7. Here n7 must divide 6 ( = 2 · 3) and n7 = 1 mod 7, so n7 = 1. So, as before, G can not be simple.

On the other hand for |G| = 60 = 22 · 3 · 5, then n3 = 10 and n5 = 6 is perfectly possible. And in fact, the smallest simple non-cyclic group is A5, the alternating group over 5 elements. It has order 60, and has 24 cyclic permutations of order 5, and 20 of order 3.

Proof of the Sylow theorems

The proofs of the Sylow theorems exploit the notion of group action in various creative ways. The group G acts on itself or on the set of its p-subgroups in various ways, and each such action can be exploited to prove one of the Sylow theorems. The following proofs are based on combinatorial arguments of H. Wielandt published in 1959. In the following, we use a | b as notation for "a divides b" and a 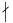\nmid b for the negation of this statement.

Theorem 1: A finite group G whose order |G| is divisible by a prime power pk has a subgroup of order pk.

Proof: Let |G| = pkm, and let pr be the maximal power of p that divides m. Let Ω denote the set of subsets of G of size pk. Clearly:

|\Omega | ={p^km \choose p^k}\mathrm{,}

pr is precisely the maximal power of p that divides |Ω|, in particular, pr+1 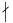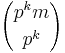\nmid {p^km \choose p^k}. Let G act on Ω by left multiplication. It follows by the choice of r that there is an element A ∈ Ω with an orbit θ = GA such that pr+1 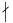\nmid |θ|. Now |θ| = |GA| = [G : GA] where GA denotes the stabilizer subgroup of the set A, hence pk | |GA| so pk ≤ |GA|. On the other hand, fix an element a ∈ A . The function [g ↦ ga] maps GA to A injectively; therefore |A| ≥ |GA|, hence |GA| = pk and GA is a desired subgroup.

Lemma: Let G be a finite p-group, let G act on a finite set Ω, and let Ω0 denote the set of points of Ω that are fixed under the action of G. Then |Ω| ≡ |Ω0| mod p.

Proof: Write Ω as a disjoint sum of its orbits under G. Any element x ∈ Ω not fixed by G will lie in an orbit of order |G|/|Gx| (where Gx denotes the stabilizer), which is a multiple of p by assumption. The result follows immediately.

Theorem 2: If H is a p-subgroup of G and P is a Sylow p-subgroup of G, then there exists an element g in G such that g−1Hg ≤ P. In particular, all Sylow p-subgroups of G are conjugate to each other (and therefore isomorphic), i.e. if H and K are Sylow p-subgroups of G, then there exists an element g in G with g−1Hg = K.

Proof: Let Ω be the set of left cosets of P in G and let H act on Ω by left multiplication. Applying the Lemma to H on Ω, we see that |Ω0| ≡ |Ω| = [G : P] mod p. Now p 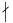\nmid [G : P] by definition so p 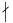\nmid |Ω0|, hence in particular |Ω0| ≠ 0 so there exists some gP ∈ Ω0. It follows that for some g ∈ G and ∀ h ∈ H we have hgP = gP so g−1hgP ⊆ P and therefore g−1Hg ≤ P. Now if H is a Sylow p-subgroup, |H| = |P| = |gPg−1| so that H = gPg−1 for some g ∈ G.

Theorem 3: Let q denote the order of any Sylow p-subgroup of a finite group G. Then np | |G|/q and np ≡ 1 mod p.

Proof: By Theorem 2, np = [G : NG(P)], where P is any such subgroup, and NG(P) denotes the normalizer of P in G, so this number is a divisor of |G|/q. Let Ω be the set of all Sylow p-subgroups of G, and let P act on Ω by conjugation. Let Q ∈ Ω0 and observe that then Q = xQx−1 for all x ∈ P so that P ≤ NG(Q). By Theorem 2, P and Q are conjugate in NG(Q) in particular, and Q is normal in NG(Q), so then P = Q. It follows that Ω0 = {P} so that, by the Lemma, |Ω| ≡ |Ω0| = 1 mod p.

Finding a Sylow subgroup

The problem of finding a Sylow subgroup of a given group is an important problem in computational group theory. In permutation groups, it has been proven by William Kantor that a Sylow p-subgroup can be found in polynomial time of the input (the degree of the group times the number of generators).

References