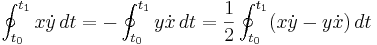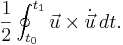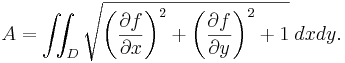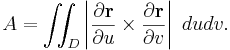Area
Area is a quantity expressing the two-dimensional size of a defined part of a surface, typically a region bounded by a closed curve. The term surface area refers to the total area of the exposed surface of a 3-dimensional solid, such as the sum of the areas of the exposed sides of a polyhedron. Area is an important invariant in the differential geometry of surfaces.
Contents |
Units
Units for measuring surface area include:
-
- are (a) = 100 square meters (m²)
- hectare (ha) = 100 ares (a) = 10000 square meters (m²)
- square kilometre (km²) = 100 hectars (ha) = 10000 ares (a) = 1000000 square metres (m²)
- square megametre (Mm²) = 1012 square metres
- square foot = 144 square inches = 0.09290304 square metres (m²)
- square yard = 9 square feet (0.84 m2) = 0.83612736 square metres (m²)
- square perch = 30.25 square yards = 25.2928526 square metres (m²)
- acre = 10 square chains or 160 square perches or 4840 square yards or 43,560 square feet (4,047 m2) = 4046.8564224 square metres (m²)
- square mile = 640 acres (2.6 km2) = 2.5899881103 squarea kilometers (km2)
Useful formulas
| Shape | Equation | Variables |
|---|---|---|
| Square | 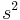 |
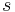 is the length of the side of the square. is the length of the side of the square. |
| Regular triangle | 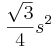 |
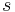 is the length of one side of the triangle. is the length of one side of the triangle. |
| Regular hexagon | 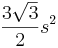 |
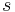 is the length of one side of the hexagon. is the length of one side of the hexagon. |
| Regular octagon | 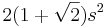 |
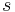 is the length of one side of the octagon. is the length of one side of the octagon. |
| Any regular polygon | 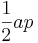 |
 is the apothem, or the radius of an inscribed circle in the polygon, and is the apothem, or the radius of an inscribed circle in the polygon, and 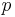 is the perimeter of the polygon. is the perimeter of the polygon. |
| Any regular polygon | 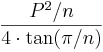 |
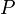 is the Perimeter and is the Perimeter and 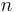 is the number of sides. is the number of sides. |
| Any regular polygon (using degree measure) | 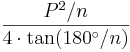 |
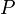 is the Perimeter and is the Perimeter and 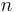 is the number of sides. is the number of sides. |
| Rectangle | 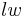 |
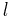 and and  are the lengths of the rectangle's sides (length and width). are the lengths of the rectangle's sides (length and width). |
| Parallelogram (in general) | 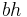 |
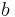 and and 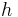 are the length of the base and the length of the perpendicular height, respectively. are the length of the base and the length of the perpendicular height, respectively. |
| Rhombus | 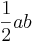 |
 and and 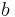 are the lengths of the two diagonals of the rhombus. are the lengths of the two diagonals of the rhombus. |
| Triangle | 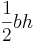 |
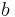 and and 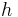 are the base and altitude (measured perpendicular to the base), respectively. are the base and altitude (measured perpendicular to the base), respectively. |
| Triangle | 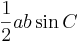 |
 and and 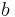 are any two sides, and are any two sides, and 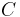 is the angle between them. is the angle between them. |
| Circle | 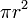 , or , or 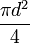 |
 is the radius and is the radius and 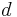 the diameter. the diameter. |
| Ellipse | 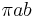 |
 and and 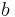 are the semi-major and semi-minor axes, respectively. are the semi-major and semi-minor axes, respectively. |
| Trapezoid | 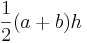 |
 and and 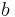 are the parallel sides and are the parallel sides and 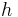 the distance (height) between the parallels. the distance (height) between the parallels. |
| Total surface area of a Cylinder | 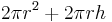 |
 and and 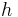 are the radius and height, respectively. are the radius and height, respectively. |
| Lateral surface area of a cylinder | 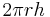 |
 and and 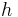 are the radius and height, respectively. are the radius and height, respectively. |
| Total surface area of a Cone | 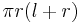 |
 and and 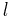 are the radius and slant height, respectively. are the radius and slant height, respectively. |
| Lateral surface area of a cone | 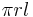 |
 and and 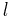 are the radius and slant height, respectively. are the radius and slant height, respectively. |
| Total surface area of a Sphere | 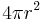 or or 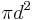 |
 and and 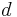 are the radius and diameter, respectively. are the radius and diameter, respectively. |
| Total surface area of an ellipsoid | See the article. | |
| Circular sector | 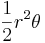 |
 and and 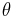 are the radius and angle (in radians), respectively. are the radius and angle (in radians), respectively. |
| Square to circular area conversion | 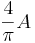 |
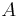 is the area of the square in square units. is the area of the square in square units. |
| Circular to square area conversion | 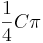 |
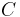 is the area of the circle in circular units. is the area of the circle in circular units. |
All of the above calculations show how to find the area of many shapes.
The area of irregular polygons can be calculated using the "Surveyor's formula".[1]
How to define area
Area is a quantity expressing the size of a figure in the Euclidean plane or on a 2-dimensional surface. Points and lines have zero area, cf. space-filling curves. A figure may have infinite area, for example the entire Euclidean plane. The 3-dimensional analog of area is the volume. Although area seems to be one of the basic notions in geometry, it is not easy to define even in the Euclidean plane. Most textbooks avoid defining an area, relying on self-evidence. For polygons in the Euclidean plane, one can proceed as follows:
- The area of a polygon in the Euclidean plane is a positive number such that:
- The area of the unit square is equal to one.
- Congruent polygons have equal areas.
- (additivity) If a polygon is a union of two polygons which do not have common interior points, then its area is the sum of the areas of these polygons.
It remains to show that the notion of area thus defined does not depend on the way one subdivides a polygon into smaller parts.
A typical way to introduce area is through the more advanced notion of Lebesgue measure. In the presence of the axiom of choice it is possible to prove the existence of shapes whose Lebesgue measure cannot be meaningfully defined. Such 'shapes' (they cannot a fortiori be simply visualised) enter into Tarski's circle-squaring problem (and, moving to three dimensions, in the Banach–Tarski paradox). The sets involved do not arise in practical matters.
In three dimensions, the analog of area is called volume. The n dimensional analog is defined by means of a measure or as a Lebesgue integral.
Additional formulas
Areas of 2-dimensional figures
- a triangle:
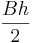 (where B is any side, and h is the distance from the line on which B lies to the other vertex of the triangle). This formula can be used if the height h is known. If the lengths of the three sides are known then Heron's formula can be used:
(where B is any side, and h is the distance from the line on which B lies to the other vertex of the triangle). This formula can be used if the height h is known. If the lengths of the three sides are known then Heron's formula can be used: 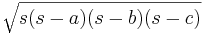 (where a, b, c are the sides of the triangle, and
(where a, b, c are the sides of the triangle, and 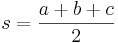 is half of its perimeter) If an angle and its two included sides are given, then area=absinC where C is the given angle and a and b are its included sides. If the triangle is graphed on a coordinate plane, a matrix can be used and is simplified to the absolute value of (x1y2+ x2y3+ x3y1 - x2y1- x3y2- x1y3) all divided by 2. This formula is also known as the shoelace formula and is an easy way to solve for the area of a coordinate triangle by substituting the 3 points, (x1,y1) (x2,y2) (x3,y 3). The shoelace formula can also be used to find the areas of other polygons when their vertices are known. Another approach for a coordinate triangle is to use Infinitesimal calculus to find the area.
is half of its perimeter) If an angle and its two included sides are given, then area=absinC where C is the given angle and a and b are its included sides. If the triangle is graphed on a coordinate plane, a matrix can be used and is simplified to the absolute value of (x1y2+ x2y3+ x3y1 - x2y1- x3y2- x1y3) all divided by 2. This formula is also known as the shoelace formula and is an easy way to solve for the area of a coordinate triangle by substituting the 3 points, (x1,y1) (x2,y2) (x3,y 3). The shoelace formula can also be used to find the areas of other polygons when their vertices are known. Another approach for a coordinate triangle is to use Infinitesimal calculus to find the area.
Area in calculus
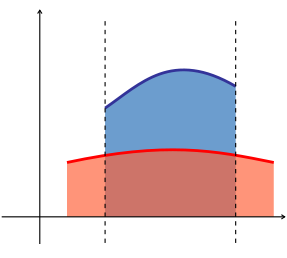
- the area between the graphs of two functions is equal to the integral of one function, f(x), minus the integral of the other function, g(x).
- an area bounded by a function r = r(θ) expressed in polar coordinates is
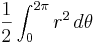 .
. - the area enclosed by a parametric curve
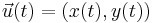 with endpoints
with endpoints  is given by the line integrals
is given by the line integrals
(see Green's theorem)
- or the z-component of
Surface area of 3-dimensional figures
- cube:
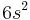 , where s is the length of the top side
, where s is the length of the top side - rectangular box:
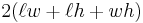 the length divided by height
the length divided by height - cone:
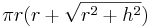 , where r is the radius of the circular base, and h is the height. That can also be rewritten as
, where r is the radius of the circular base, and h is the height. That can also be rewritten as 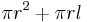 where r is the radius and l is the slant height of the cone.
where r is the radius and l is the slant height of the cone. 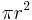 is the base area while
is the base area while 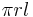 is the lateral surface area of the cone.
is the lateral surface area of the cone. - prism: 2 * Area of Base + Perimeter of Base * Height
General formula
The general formula for the surface area of the graph of a continuously differentiable function 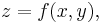 where
where 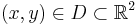 and
and 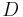 is a region in the xy-plane with the smooth boundary:
is a region in the xy-plane with the smooth boundary:
Even more general formula for the area of the graph of a parametric surface in the vector form 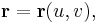 where
where 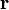 is a continuously differentiable vector function of
is a continuously differentiable vector function of 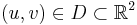 :
:
Area minimisation
Given a wire contour, the surface of least area spanning ("filling") it is a minimal surface. Familiar examples include soap bubbles.
The question of the filling area of the Riemannian circle remains open.