Subset

Euler diagram showing
A is a subset of B and conversely B is a superset of A

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. Notice that A and B may coincide. The relationship of one set being a subset of another is called inclusion.

Definitions

If A and B are sets and every element of A is also an element of B, then:

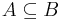• A is a subset of (or is included in) B, denoted by ,

or equivalently

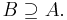
• B is a superset of (or includes) A, denoted by

If A is a subset of B, but A is not equal to B (i.e. there exists at least one element of B not contained in A), then

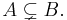
• A is also a proper (or strict) subset of B; this is written as

or equivalently

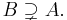
• B is a proper superset of A; this is written as

For any set S, the inclusion relation ⊆ is a partial order on the set 2^S of all subsets of S (the power set of S).

The symbols ⊂ and ⊃

Some authors use the symbols ⊂ and ⊃ to indicate "subset" and "superset" respectively, instead of the symbols ⊆ and ⊇, but with the same meaning. So for example, for these authors, it is true of every set A that A ⊂ A.

Other authors prefer to use the symbols ⊂ and ⊃ to indicate proper subset and superset, respectively, in place of 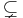and 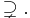This usage makes ⊆ and ⊂ analogous to ≤ and <. For example, if x ≤ y then x may be equal to y, or maybe not, but if x < y, then x definitely does not equal y, but is strictly less than y. Similarly, using the "⊂ means proper subset" convention, if A ⊆ B, then A may or may not be equal to B, but if A ⊂ B, then A is definitely not equal to B.

Examples

• The set {1, 2} is a proper subset of {1, 2, 3}.
• Any set is a subset of itself, but not a proper subset.
• The empty set, written ∅, is also a subset of any given set X. (This statement is vacuously true.) The empty set is always a proper subset, except of itself.
• The set {x: x is a prime number greater than 2000} is a proper subset of {x: x is an odd number greater than 1000}
• The set of natural numbers is a proper subset of the set of rational numbers and the set of points in a line segment is a proper subset of the set of points in a line. These are counter-intuitive examples in which both the part and the whole are infinite, and the part has the same number of elements as the whole (see Cardinality of infinite sets).

Other properties of inclusion

Inclusion is the canonical partial order in the sense that every partially ordered set (X, 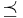) is isomorphic to some collection of sets ordered by inclusion. The ordinal numbers are a simple example—if each ordinal n is identified with the set [n] of all ordinals less than or equal to n, then a ≤ b if and only if [a] ⊆ [b].

For the power set 2^S of a set S, the inclusion partial order is (up to an order isomorphism) the Cartesian product of k = |S| (the cardinality of S) copies of the partial order on {0,1} for which 0 < 1. This can be illustrated by enumerating S = {s₁, s₂, …, s_k} and associating with each subset T ⊆ S (which is to say with each element of 2^S) the k-tuple from {0,1}^k of which the ith coordinate is 1 if and only if s_i is a member of T.

References

• Jech, Thomas (2002). Set Theory. Springer-Verlag. ISBN 3-540-44085-2.