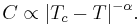Phase transition
- See also: List of states of matter
In thermodynamics, a phase transition is the transformation of a thermodynamic system from one phase to another.
At phase-transition point, physical properties may undergo abrupt change- for instance, volume of the two phases may be vastly different. As an example imagine transition of liquid water into vapour at boiling point.
In the English vernacular, the term is most commonly used to describe transitions between solid, liquid and gaseous states of matter, in rare cases including plasma.
Contents |
Types of phase transition
Examples of phase transitions include:
- The transitions between the solid, liquid, and gaseous phases of a single component, due to the effects of temperature and/or pressure:
-
To From Solid Liquid Gas Plasma Solid Solid-Solid Transformation Melting/Fusion[1] Sublimation N/A Liquid Freezing N/A Boiling/Evaporation N/A Gas Deposition Condensation N/A Ionization Plasma N/A N/A Recombination/Deizonization N/A
-
- (see also vapor pressure and phase diagram)


- A eutectic transformation, in which a two component single phase liquid is cooled and transforms into two solid phases. The same process, but beginning with a solid instead of a liquid is called a eutectoid transformation.
- A peritectic transformation, in which a two component single phase solid is heated and transforms into a solid phase and a liquid phase.
- A spinodal decomposition, in which a single phase is cooled and separates into two different compositions of that same phase.
- The transition between the ferromagnetic and paramagnetic phases of magnetic materials at the Curie point.
- The transition between differently ordered, commensurate or incommensurate, magnetic structures, such as in cerium antimonide.
- The martensitic transformation which occurs as one of the many phase transformations in carbon steel and stands as a model for displacive phase transformations.
- Changes in the crystallographic structure such as between ferrite and austenite of iron.
- Order-disorder transitions such as in alpha-titanium aluminides.
- The emergence of superconductivity in certain metals when cooled below a critical temperature.
- The transition between different molecular structures (polymorphs or allotropes), especially of solids, such as between an amorphous structure and a crystal structure or between two different crystal structures.
- Quantum condensation of bosonic fluids, such as Bose-Einstein condensation and the superfluid transition in liquid helium.
- The breaking of symmetries in the laws of physics during the early history of the universe as its temperature cooled.
- Phase transitions in intractable computational complexity problems such as NP-complete or PSPACE problems. For example it has been noticed in k-SAT problems that the transition from solvable to unsolvable instances exhibits threshold behavior depending on the ratio of number of clauses to number of variables. Moreover, the amount of computational time required to solve the problem or determine it to be unsolvable increases drastically around the threshold. This line of research comes mostly from investigating similarities between computational complexity and statistical physics.
Phase transitions happen when the free energy of a system is non-analytic for some choice of thermodynamic variables - see phases. This non-analyticity generally stems from the interactions of an extremely large number of particles in a system, and does not appear in systems that are too small.
To put it simply, at phase-transition point (for instance, boiling point for water) the two phases of water - liquid and vapour have identical free energies and therefore are equally likely to exist. Below the boiling point, liquid-water is more stable state of the two. At boiling point liquid and vapour are equally stable and above boiling point vapour is more stable than liquid state of water.
It is sometimes possible to change the state of a system non-adiabatically in such a way that it can be brought past a phase transition point without undergoing a phase transition. The resulting state is metastable i.e. not theoretically stable, but quasistable. See superheating, supercooling and supersaturation.
Magnetic phases
Often also magnetic phases are used as the basis of a theory, and for introductory motivation. However, usually these are similar to the well-known liquid ( ferromagnetic) or gaseous (
ferromagnetic) or gaseous ( paramagnetic) phases, as can be seen by the two equivalent interpretations, the magnetic one ("up" or "down" spins) or the lattice-gas interpretation ("occupied" or "unoccupied" sites) of a prominent binary model, the Ising model.
paramagnetic) phases, as can be seen by the two equivalent interpretations, the magnetic one ("up" or "down" spins) or the lattice-gas interpretation ("occupied" or "unoccupied" sites) of a prominent binary model, the Ising model.
Therefore we can adhere to the above table of examples.
Classification of phase transitions
Ehrenfest classification
The first attempt at classifying phase transitions was the Ehrenfest classification scheme, which grouped phase transitions based on the degree of non-analyticity involved.
In other words, even though the chemical potential of the component undergoing phase transition remains unchanged, its derivative with respect to a state variable (for instance temperature) changes. The nature of this change is the basis of Ehrenfest classification scheme.
Though useful, Ehrenfest's classification is flawed, as will be discussed in the next section.
Under this scheme, phase transitions were labeled by the lowest derivative of the free energy that is discontinuous at the transition. First-order phase transitions exhibit a discontinuity in the first derivative of the free energy with a thermodynamic variable. The various solid/liquid/gas transitions are classified as first-order transitions because they involve a discontinuous change in density (which is the first derivative of the free energy with respect to chemical potential.) Second-order phase transitions are continuous in the first derivative but exhibit discontinuity in a second derivative of the free energy. These include the ferromagnetic phase transition in materials such as iron, where the magnetization, which is the first derivative of the free energy with the applied magnetic field strength, increases continuously from zero as the temperature is lowered below the Curie temperature. The magnetic susceptibility, the second derivative of the free energy with the field, changes discontinuously. Under the Ehrenfest classification scheme, there could in principle be third, fourth, and higher-order phase transitions.
Modern classification of phase transitions
The Ehrenfest scheme is an inaccurate method of classifying phase transitions, for it does not take into account the case where a derivative of free energy diverges (which is only possible in the thermodynamic limit). For instance, in the ferromagnetic transition, the heat capacity diverges to infinity.
In the modern classification scheme, phase transitions are divided into two broad categories, named similarly to the Ehrenfest classes:
The first-order phase transitions are those that involve a latent heat. During such a transition, a system either absorbs or releases a fixed (and typically large) amount of energy. During this process, the temperature of the system will stay constant as heat is added.
Because energy cannot be instantaneously transferred between the system and its environment, first-order transitions are associated with "mixed-phase regimes" in which some parts of the system have completed the transition and others have not. This phenomenon is familiar to anyone who has boiled a pot of water: the water does not instantly turn into gas, but forms a turbulent mixture of water and water vapor bubbles. Mixed-phase systems are difficult to study, because their dynamics are violent and hard to control. However, many important phase transitions fall in this category, including the solid/liquid/gas transitions and Bose-Einstein condensation.
The second class of phase transitions are the continuous phase transitions, also called second-order phase transitions. These have no associated latent heat. Examples of second-order phase transitions are the ferromagnetic transition, superconductor and the superfluid transition. Lev Landau gave a phenomenological theory of second order phase transitions.
An example of such a second-order phase transition is the glass transition of polymeric materials which occurs at glass transition temperature Tg of the polymer, and that is the reason why Tg can be identified easily as a change in the slope of the heating energy vs. temperature curve that results from the measurement of Tg on Differential scanning calorimetry (DSC) while the first-order phase transition of melting point Tm looks as a clear peak on the same graph.
Several transitions are known as the infinite-order phase transitions. They are continuous but break no symmetries. The most famous example is the Kosterlitz-Thouless transition in the two-dimensional XY model. Many quantum phase transitions in two-dimensional electron gases belong to this class.
Properties of phase transitions
Critical points
In any system containing liquid and gaseous phases, there exists a special combination of pressure and temperature, known as the critical point, at which the transition between liquid and gas becomes a second-order transition. Near the critical point, the fluid is sufficiently hot and compressed that the distinction between the liquid and gaseous phases is almost non-existent.
This is associated with the phenomenon of critical opalescence, a milky appearance of the liquid, due to density fluctuations at all possible wavelengths (including those of visible light).
Symmetry
Phase transitions often (but not always) take place between phases with different symmetry. Consider, for example, the transition between a fluid (i.e. liquid or gas) and a crystalline solid. A fluid, which is composed of atoms arranged in a disordered but homogeneous manner, possesses continuous translational symmetry: each point inside the fluid has the same properties as any other point. A crystalline solid, on the other hand, is made up of atoms arranged in a regular lattice. Each point in the solid is not similar to other points, unless those points are displaced by an amount equal to some lattice spacing.
Generally, we may speak of one phase in a phase transition as being more symmetrical than the other. The transition from the more symmetrical phase to the less symmetrical one is a symmetry-breaking process. In the fluid-solid transition, for example, we say that continuous translation symmetry is broken.
The ferromagnetic transition is another example of a symmetry-breaking transition, in this case the symmetry under reversal of the direction of electric currents and magnetic field lines. This symmetry is referred to as "up-down symmetry" or "time-reversal symmetry". It is broken in the ferromagnetic phase due to the formation of magnetic domains containing aligned magnetic moments. Inside each domain, there is a magnetic field pointing in a fixed direction chosen spontaneously during the phase transition. The name "time-reversal symmetry" comes from the fact that electric currents reverse direction when the time coordinate is reversed.
The presence of symmetry-breaking (or nonbreaking) is important to the behavior of phase transitions. It was pointed out by Landau that, given any state of a system, one may unequivocally say whether or not it possesses a given symmetry. Therefore, it cannot be possible to analytically deform a state in one phase into a phase possessing a different symmetry. This means, for example, that it is impossible for the solid-liquid phase boundary to end in a critical point like the liquid-gas boundary. However, symmetry-breaking transitions can still be either first- or second-order.
Typically, the more symmetrical phase is on the high-temperature side of a phase transition, and the less symmetrical phase on the low-temperature side. This is certainly the case for the solid-fluid and ferromagnetic transitions. This happens because the Hamiltonian of a system usually exhibits all the possible symmetries of the system, whereas the low-energy states lack some of these symmetries (this phenomenon is known as spontaneous symmetry breaking). At low temperatures, the system tends to be confined to the low-energy states. At higher temperatures, thermal fluctuations allow the system to access states in a broader range of energy, and thus more of the symmetries of the Hamiltonian.
Symmetries which are only present at low temperatures are called accidental symmetries. For example, a symmetry which is broken by a process which requires a lot of energy, such as the creation of heavy virtual particles, is an accidental symmetry at temperatures sufficiently low that this process is suppressed.
Order parameters
The order parameter is normally a quantity which is 0 in one phase, usually above the critical point and non-zero in the other. It characterises the onset of order at the phase transition. The order parameter susceptibility will usually diverge approaching the critical point. For a ferromagnetic system undergoing a phase transition, the order parameter is the net magnetization. For solid/liquid or liquid/gas transitions, it is the density.
When symmetry is broken, one needs to introduce one or more extra variables to describe the state of the system. For example, in the ferromagnetic phase, one must provide the net magnetization, whose direction was spontaneously chosen when the system cooled below the Curie point. Such variables are examples of order parameters. An order parameter is a measure of the degree of order in a system; the extreme values are 0 for total disorder and 1 for complete order.[2] For example, an order parameter can indicate the degree of order in a liquid crystal. However, note that order parameters can also be defined for non-symmetry-breaking transitions.
There also exist dual descriptions of phase transitions in terms of disorder parameters. These indicate the presence of line-like excitations such as vortex- or defect lines.
Relevance for cosmology
Symmetry-breaking phase transitions play an important role in cosmology. It has been speculated that, in the hot early universe, the vacuum (i.e. the various quantum fields that fill space) possessed a large number of symmetries. As the universe expanded and cooled, the vacuum underwent a series of symmetry-breaking phase transitions. For example, the electroweak transition broke the SU(2)×U(1) symmetry of the electroweak field into the U(1) symmetry of the present-day electromagnetic field. This transition is important to understanding the asymmetry between the amount of matter and antimatter in the present-day universe (see electroweak baryogenesis.)
Progressive phase transitions in an expanding universe are implicated in the development of order in the universe, as is illustrated by the work of Eric Chaisson[3] and David Layzer [4]. See also Relational order theories.
- See also: order-disorder
Critical exponents and universality classes
Continuous phase transitions are easier to study than first-order transitions due to the absence of latent heat, and they have been discovered to have many interesting properties. The phenomena associated with continuous phase transitions are called critical phenomena, due to their association with critical points.
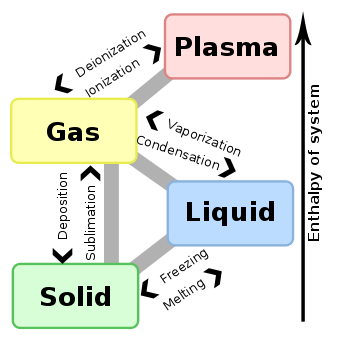
It turns out that continuous phase transitions can be characterized by parameters known as critical exponents. The most important one is perhaps the exponent describing the divergence of the thermal correlation length by approaching the transition. For instance, let us examine the behavior of the heat capacity near such a transition. We vary the temperature T of the system while keeping all the other thermodynamic variables fixed, and find that the transition occurs at some critical temperature Tc. When T is near Tc, the heat capacity C typically has a power law behaviour:
A similar behaviour, but with the exponent  instead of
instead of  , applies for the correlation length.
, applies for the correlation length.
The exponent  is positive. This is different with
is positive. This is different with  . Its actual value depends on the type of phase transition we are considering.
. Its actual value depends on the type of phase transition we are considering.
For -1 < α < 0, the heat capacity has a "kink" at the transition temperature. This is the behavior of liquid helium at the lambda transition from a normal state to the superfluid state, for which experiments have found α = -0.013±0.003. At least one experiment was performed in the zero-gravity conditions of an orbiting satellite to minimize pressure differences in the sample (see here). This experimental value of α agrees with theoretical predictions based on variational perturbation theory (see here).
For 0 < α < 1, the heat capacity diverges at the transition temperature (though, since α < 1, the divergence is not strong enough to produce a latent heat). An example of such behavior is the 3-dimensional ferromagnetic phase transition. In the three-dimensional Ising model for uniaxial magnets, detailed theoretical studies have yielded the exponent α ∼ +0.110.
Some model systems do not obey a power-law behavior. For example, mean field theory predicts a finite discontinuity of the heat capacity at the transition temperature, and the two-dimensional Ising model has a logarithmic divergence. However, these systems are limiting cases and an exception to the rule. Real phase transitions exhibit power-law behavior.
Several other critical exponents - β, γ, δ, ν, and η - are defined, examining the power law behavior of a measurable physical quantity near the phase transition. Exponents are related by scaling relations such as 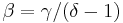 ,
, 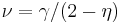 . It can be shown that there are only two independent exponents, e.g.
. It can be shown that there are only two independent exponents, e.g.  and
and 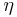 .
.
It is a remarkable fact that phase transitions arising in different systems often possess the same set of critical exponents. This phenomenon is known as universality. For example, the critical exponents at the liquid-gas critical point have been found to be independent of the chemical composition of the fluid. More amazingly, but understandable from above, they are an exact match for the critical exponents of the ferromagnetic phase transition in uniaxial magnets. Such systems are said to be in the same universality class. Universality is a prediction of the renormalization group theory of phase transitions, which states that the thermodynamic properties of a system near a phase transition depend only on a small number of features, such as dimensionality and symmetry, and are insensitive to the underlying microscopic properties of the system. Again, the divergency of the correlation length is the essential point.
Critical slowing down and other phenomena
There are also other critical phenoma; e.g., besides static functions usually there is also the critical dynamics . As a consequence, at a phase transition one may observe critical slowing down or speeding up, respectively. As a consequence, the large static universality classes of a continuous phase transition split into smaller dynamic universality classes. Furthermore, in addition to the critical exponents there are also universal relations for certain static or dynamic functions of the magnetic fields and temperature differences from the critical value.
Phase-change data storage
Several data-storage technologies use chalcogenide glass, which can be "switched" between two states, crystalline or amorphous, with the application of heat.
Phase change and optical disc technology
Phase change technology is also used to write to optical discs, such as CD-RW or DVD-RW discs. This is accomplished by including both a read laser and a more powerful write laser inside the drive. The discs contain a layer of a crystalline material that, when hit by a pulse of laser light from the write laser, changes to an amorphous state, thus changing its reflectivity. A different pulse level will reverse the changes, thus erasing the recorded information. The read laser is not powerful enough to induce a phase change, but can be used by the drive to tell whether a bit is "on" or "off" based on an area of the disc's reflectivity.
History of phase change optical disc technology
- 1990: LF 7010 by Panasonic, store 472 MB per side.
- 1995: PD (Phasewriter Dual) by Panasonic, store 650 MB.
- 1996: CD-RW (Compact Disc ReWritable) by Philips, Sony, Hewlett-Packard, Mitsubishi Chemical Corp. and Ricoh, store initially 650 MB and later 700 MB.
- 1998: DVD-RAM (DVD-Random Access Memory) by Panasonic, store initially 2.6 GB and later 4.7 GB.
- 199x: DVD±RW (DVD-ReWritable) by supplier consortium, store 4.7 GB.
- 2004: PDD (Professional Disc for Data) by Sony, store 20.5 GB.
- 2004: UDO (Ultra Density Optical) by Plasmon, store 28 GB.
- 2006: BD-RE (Blu-ray Disc Rerecordable) by Sony, store 50 GB.
Phase-change memory
Phase-change memory (PRAM) is a kind of non-volatile computer memory. Prototype PRAM devices have demonstrated higher density and faster write times than flash memory.
PRAM uses chalcogenide glass, the same material utilized in re-writable optical media (such as CD-RW and DVD-RW). The amorphous, high resistance state is used to represent a binary 1, and the crystalline, low resistance state represents a 0.
Samsung, Intel, and STMicroelectronics demonstrated prototype PRAM devices in 2006, and announced plans for commercial productions.
See also
- Crystal growth
- Differential scanning calorimetry
- Lambda transition universality class
- Landau theory of second order phase transitions
- Laser-heated pedestal growth
- Superfluid film
- Autocatalytic reactions and order creation
References
- ↑ Chang, R., Chemistry, 7th Ed, McGraw-Hill (2002)
- ↑ A. D. McNaught and A. Wilkinson, ed.. Compendium of Chemical Terminology (commonly called The Gold Book). IUPAC. ISBN 0-86542-684-8. http://www.iupac.org/goldbook/O04323.pdf. Retrieved on 2007-10-23.
- ↑ Chaisson, “Cosmic Evolution”, Harvard, 2001
- ↑ David Layzer, Cosmogenesis, The Development of Order in the Universe", Oxford Univ. Press, 1991
General references
- Anderson, P.W., Basic Notions of Condensed Matter Physics, Perseus Publishing (1997).
- Goldenfeld, N., Lectures on Phase Transitions and the Renormalization Group, Perseus Publishing (1992).
- Krieger, Martin H., Constitutions of matter : mathematically modelling the most everyday of physical phenomena, University of Chicago Press, 1996. Contains a detailed pedagogical discussion of Onsager's solution of the 2-D Ising Model.
- Landau, L.D. and Lifshitz, E.M., Statistical Physics Part 1, vol. 5 of Course of Theoretical Physics, Pergamon, 3rd Ed. (1994).
- Kleinert, H., Critical Properties of φ4-Theories, World Scientific (Singapore, 2001); Paperback ISBN 9810246595 (readable online here).
- Kleinert, H. and Verena Schulte-Frohlinde, Gauge Fields in Condensed Matter, Vol. I, "SUPERFLOW AND VORTEX LINES; Disorder Fields, Phase Transitions,", pp. 1--742, World Scientific (Singapore, 1989); Paperback ISBN 9971-5-0210-0 (readable online here)
- Schroeder, Manfred R., Fractals, chaos, power laws : minutes from an infinite paradise, New York: W.H. Freeman, 1991. Very well-written book in "semi-popular" style -- not a textbook -- aimed at an audience with some training in mathematics and the physical sciences. Explains what scaling in phase transitions is all about, among other things.
External links
- Interactive Phase Transitions on lattices with Java applets
|
||||||||||||||||||||||