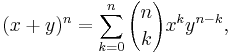Ring (mathematics)
In mathematics, a ring is an algebraic structure which generalizes the algebraic properties of the integers, though the rational, real and complex numbers are also all rings. Rings, unlike groups, contain two binary operations usually called addition and multiplication. The branch of abstract algebra which studies rings is called ring theory.
Contents[hide] |
Motivation
In mathematics, objects commonly arise which have structure similar to the integers, but may behave differently in some ways. For example, matrices can be added and multiplied as expected, but such multiplication does not in general satisfy the commutative law. As a different example, the integers modulo n satisfy similar laws of arithmetic but have zero divisors if n is not prime.
A ring is an abstraction of certain properties of the integers that is general enough to allow the study of a greater variety of objects, but strong enough to ensure a rich theory in which substantial results can be proven. In a sense, rings have more structure than an abelian group but less than a field. That is, every field is also a ring and every ring is also an abelian group.
Definition
A ring is a set R equipped with two binary operations + : R × R → R and · : R × R → R (where × denotes the Cartesian product), called addition and multiplication, such that:
- (R, +) is an abelian group with identity element 0, meaning that for all a, b, c in R, the following axioms hold:
- (a + b) + c = a + (b + c) (+ is associative)
- 0 + a = a (0 is the identity)
- a + b = b + a (+ is commutative)
- for each a in R there exists −a in R such that a + (−a) = (−a) + a = 0 (−a is the inverse element of a)
- (R, ·) is a monoid with identity element 1, meaning that for all a, b, c in R, the following axioms hold:
- (a ⋅ b) ⋅ c = a ⋅ (b ⋅ c) (⋅ is associative)
- 1 ⋅ a = a ⋅ 1 = a (1 is the identity)
- Multiplication distributes over addition:
- a ⋅ (b + c) = (a ⋅ b) + (a ⋅ c)
- (a + b) ⋅ c = (a ⋅ c) + (b ⋅ c).
As with groups the symbol ⋅ is usually omitted and multiplication is just denoted by juxtaposition. Also, the standard order of operation rules are used, so that, for example, a + bc is an abbreviation for a + (b ⋅ c).
Although ring addition is commutative, so that a + b = b + a, ring multiplication is not required to be commutative; a ⋅ b need not equal b ⋅ a. Rings that also satisfy commutativity for multiplication (such as the ring of integers) are called commutative rings. An example of a non-commutative ring is the ring of n × n matrices over a field K, for n > 1.
Rings need not have multiplicative inverses either. An element a in a ring is called a unit if it is invertible with respect to multiplication: if there is an element b in the ring such that a·b = b·a = 1, then b is uniquely determined by a and we write a−1 = b. The set of all units in R forms a group under ring multiplication; this group is denoted by U(R) or R*.
Alternative definitions
There are some alternative definitions of rings of which the reader should be aware:
- Some authors add the additional requirement that 0 ≠ 1. This excludes only one ring: the so called trivial ring, which has only a single element.
- A more significant difference is that some authors omit the requirement that a ring have a multiplicative identity.[1][2] These authors call rings which do have multiplicative identities unital rings, unitary rings, or simply rings with unity or rings with identity. Authors such as Bourbaki, who do require rings to have a multiplicative identity, call algebraic objects which meet all the requirements of a ring except possibly the unity requirement pseudo-rings. The term rng (jocular; ring without the multiplicative identity) has also been used. The even integers are an example of a pseudo-ring. Any non-unitary ring R can be embedded in a canonical way as a sub-pseudo-ring of a unitary ring, namely R ⊕ Z with multiplication defined by (x, m) ⋅ (y, n) = (xy + my + nx, mn), so that (0, 1) is a multiplicative identity. This process is said to adjoin a unit element to R. If the same construction of adjoining a unit is applied to unitary ring R, the result is a different ring, with a new unit element. (See Unital.)
- Similarly, the requirement for the ring multiplication to be associative is sometimes dropped, and rings in which the associative law holds are then called associative rings. See nonassociative rings for a discussion of the more general situation.
As noted above, multiplication in a ring need not be commutative. Some fields such as commutative algebra and algebraic geometry are primarily concerned with commutative rings. Mathematicians writing in those areas (such as Alexander Grothendieck in Éléments de géométrie algébrique) frequently use the word ring to mean "commutative ring" by convention, and not necessarily commutative ring to mean "ring".
In this article all rings are assumed to be associative and unital unless otherwise stated.
Examples
- The trivial ring {0} has only one element, and it serves both as the additive and the multiplicative identity.
- The motivating example is the ring of integers with the two operations of addition and multiplication. This is a commutative ring.
- The rational, real and complex numbers form rings (in fact, they are even fields). These are likewise commutative rings.
- Every field is by definition a commutative ring.
- The Gaussian integers form a ring, as do the Eisenstein integers. So does their generalization Kummer ring.
- The polynomial ring R[X] of polynomials over a ring R is also a ring.
- The set of formal power series R[[X1, …, Xn]] over a commutative ring R is a ring.
- Example of a noncommutative ring: For any ring R and any natural number n, the set of all square n-by-n matrices with entries from R, forms a ring with matrix addition and matrix multiplication as operations. For n=1, this matrix ring is just (isomorphic to) R itself. For n>1, this matrix ring is an example of a noncommutative ring (unless R is the trivial ring).
- Example of a finite ring: If n is a positive integer, then the set Zn = Z/nZ of integers modulo n (as an additive group the cyclic group of order n) forms a ring with n elements (see modular arithmetic). If n=1, then Z/nZ is the trivial ring.
- If S is a set, then the power set of S becomes a ring if we define addition to be the symmetric difference of sets and multiplication to be intersection. This corresponds to a ring of sets and is an example of a Boolean ring.
- The set of all continuous real-valued functions defined on the interval [a, b] forms a ring (even an associative algebra). The operations are addition and multiplication of functions.
- If G is an abelian group, then the endomorphisms of G form a ring, the endomorphism ring End(G) of G. The operations in this ring are addition and composition of endomorphisms.
- If G is a group and R is a ring, the group ring of G over R is a free module over R having G as basis. Multiplication is defined by the rules that the elements of G commute with the elements of R and multiply together as they do in the group G.
- Non-example: The set of natural numbers N is not a ring, since (N, +) is not even a group (the elements are not all invertible with respect to addition). For instance, there is no natural number which can be added to 3 to get 0 as a result. There is a natural way to make it a ring by adding negative numbers to the set, thus obtaining the ring of integers. The natural numbers (including 0) form an algebraic structure known as a semiring (which has all of the properties of a ring except the additive inverse property).
- The even numbers 2Z (including negative even numbers) are an example of a pseudo-ring in that they have all the properties of a ring except a multiplicative identity.
- Ring of dual numbers: Let є be a formal symbol and F a field. The ring of dual numbers, F[є], is defined as F[є] = {a + bє : a, b in F},with the following addition and multiplication:
(a + bє) + (c + dє) = a + c + (b + d)є
(a + bє)(c + dє) = ac + (ad + bc)є
Note that є is a zero divisor: є ≠ 0 but є2 = 0. - Ring of split-complex numbers: z = x + y j , j2 = +1. A ring analogous to the ordinary complex plane but substitutes conjugate hyperbolas for the unit circle.
Basic theorems
From the axioms, one can immediately deduce that if R is a ring, for all a, b in R we have:
- 0 ⋅ a = a ⋅ 0 = 0
- (−1)a = −a
- (−a)b = a(−b) = −(ab)
- (ab)−1 = b−1a−1 if both a and b are invertible.
Other basic theorems
- The identity element 1 is unique.
- If a ring element has a multiplicative inverse, then the inverse is unique.
- If the ring has at least two elements then 0 ≠ 1.
- If n is an integer, and a an element of the ring define na as one would by viewing a as an element of the additive group of the ring (that is, 0 if n is 0, the sum of n copies of a if n is positive, and the opposite of (−n)a if n is negative.) We usually write n for the ring element n1. Then:
- The two definitions of na coincide, that is, first, with n viewed as an integer as above; second, with n meaning the ring element n1 and multiplication in the expression na taking place in the ring. Thus the integer n may be identified with the ring element n. (Except that more than one integer may correspond to a single ring element this way.)
- The ring element n commutes with all other elements of the ring.
- If m and n are integers and a and b are ring elements, then (m ⋅ a)(n ⋅ b) = (mn) ⋅ (ab)
- If n is an integer and a is a ring element, then n ⋅ (−a) = −(n ⋅ a)
- The binomial theorem
- holds whenever x and y commute. The theorem holds for arbitrary x and y in a commutative ring.
- If a ring is a cyclic group under addition, then it is commutative.
Constructing new rings from given ones
- For every ring R we can define the opposite ring Rop by reversing the multiplication in R. Given the multiplication · in R the multiplication ∗ in Rop is defined as b ∗ a := a ⋅ b. The "identity map" from R to Rop is an isomorphism if and only if R is commutative. However, even if R is not commutative, it is still possible for R and Rop to be isomorphic. For example, if R is the ring of n × n matrices of real numbers, then the transposition map from R to Rop is an isomorphism.
- If a subset S of a ring R is closed under multiplication, addition and subtraction and contains the additive and multiplicative identity elements, then S is called a subring of R.
- The center of a ring R is the set of elements of R that commute with every element of R; that is, c lies in the center if cr = rc for every r in R. The center is a subring of R. We say that a subring S of R is central if it is a subring of the center of R.
- The direct product of two rings R and S is the cartesian product R×S together with the operations
- (r1, s1) + (r2, s2) = (r1 + r2, s1 + s2) and
- (r1, s1)(r2, s2) = (r1r2, s1s2).
- More generally, for any index set J and collection of rings (Rj)j ∈ J, there is a direct product ring. The direct product is the collection of "infinite-tuples" (rj)j ∈ J with component-wise addition and multiplication. More formally, let U be the union of all of the rings Rj. Then the direct product of the Rj over all j ∈ J is the set of all maps r : J → U with the property that rj ∈ Rj. Addition and multiplication of these functions is via the addition and multiplication in each individual Rj. Thus
- (r + s)j = rj + sj and (rs)j = rjsj.
- Given a ring R and an two-sided ideal I of R, the quotient ring (or factor ring) R/I is the set of cosets of I together with the operations
- (a + I) + (b + I) = (a + b) + I and
- (a + I)(b + I) = (ab) + I.
- Since any ring is both a left and right module over itself, it is possible to construct the tensor product of R over a ring S with another ring T to get another ring provided S is a central subring of R and T.
Categorical description
Rings can be thought of as monoids in Ab, the category of abelian groups (thought of as a monoidal category under the tensor product). The monoid action of a ring R on a abelian group is simply an R-module.
It follows that a ring may be regarded as a preadditive category (a category enriched over Ab) with a single object. Here the morphisms are the ring elements, composition of morphisms is ring multiplication, and the additive structure on morphisms is ring addition. The opposite ring is then the categorical dual.
See also
- Ring theory
- Glossary of ring theory
- Category of rings
- Algebra over a commutative ring
- Nonassociative ring
- Algebraic structure
- Special types of rings:
- Boolean ring
- Commutative ring
- Ordered ring
- Differential ring
- Division ring
- Field
- Integral domain (ID)
- Principal ideal domain (PID)
- Unique factorization domain (UFD)
- Zero ring