Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric. When a topological space has a topology that can be described by a metric, we say that that topological space is metrizable.
In differential geometry, the word "metric" is also used to refer to a structure defined only on a vector space which is more properly termed a metric tensor (or Riemannian or pseudo-Riemannian metric).
Contents |
Definition
A metric on a set X is a function (called the distance function or simply distance)
d : X × X → R
(where R is the set of real numbers). For all x, y, z in X, this function is required to satisfy the following conditions:
- d(x, y) ≥ 0 (non-negativity)
- d(x, y) = 0 if and only if x = y (identity of indiscernibles. Note that condition 1 and 2 together produce positive definiteness)
- d(x, y) = d(y, x) (symmetry)
- d(x, z) ≤ d(x, y) + d(y, z) (subadditivity / triangle inequality).
These axioms are not independent: Non-negativity follows from the other axioms.
A metric is called an ultrametric if it satisfies the following stronger version of the triangle inequality:
- For all x, y, z in M, d(x, z) ≤ max(d(x, y), d(y, z))
A metric d on X is called intrinsic if any two points x and y in X can be joined by a curve with length arbitrarily close to d(x, y).
For sets on which an addition + : X × X → X is defined, d is called a translation invariant metric if
- d(x, y) = d(x + a, y + a)
for all x, y and a in X.
Notes
These conditions express intuitive notions about the concept of distance. For example, that the distance between distinct points is positive and the distance from x to y is the same as the distance from y to x. The triangle inequality means that the distance traversed directly between x and z, is not larger than the distance to traverse in going first from x to y, and then from y to z. Euclid in his work stated that the shortest distance between two points is a line; that was the triangle inequality for his geometry.
Property 1 (d(x, y) ≥ 0) follows from properties 2, 3 and 4 and does not have to be required separately.
If a modification of the triangle inequality
- 4*. d(x, z) ≤ d(z, y) + d(y, x)
is used in the definition then property 1 follows straight from property 4*. Properties 2 and 4* give property 3 which in turn gives property 4.
Examples
- The discrete metric: if x = y then d(x,y) = 0. Otherwise, d(x,y) = 1.
- The Euclidean metric is translation and rotation invariant.
- The taxicab metric is translation invariant.
- More generally, any metric induced by a norm (see below) is translation invariant.
- If (pn)n∈N is a sequence of seminorms defining a (locally convex) topological vector space E, then
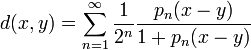
- is a metric defining the same topology. (One can replace
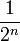 by any summable sequence
by any summable sequence 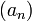 of strictly positive numbers.)
of strictly positive numbers.)
- Graph metric, a metric defined in terms of distances in a certain graph.
- The Hamming distance in coding theory.
Equivalence of metrics
For a given set X, two metrics d1 and d2 are called topologically equivalent (uniformly equivalent) if the identity mapping
- id: (X,d1) → (X,d2)
is a homeomorphism (uniform isomorphism).
For example, if 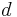 is a metric, then
is a metric, then 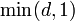 and
and 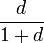 are metrics equivalent to
are metrics equivalent to 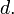
See also notions of metric space equivalence.
Metrics on vector spaces
Norms on vector spaces are equivalent to certain metrics, namely homogeneous, translation invariant ones. In other words, every norm determines a metric, and some metrics determine a norm.
Given a normed vector space (X,||.||) we can define a metric on X by
- d(x,y):=||x-y||.
The metric d is said to be induced by the norm ||.||.
Conversely if a metric d on a vector space X satisfies the properties
- d(x,y) = d(x+a,y+a) (translation invariance)
- d(αx,αy) = |α|d(x,y) (homogeneity)
then we can define a norm on X by
- ||x||:=d(x,0)
Similarly, a seminorm induces a pseudometric (see below), and a homogeneous, translation invariant pseudometric induces a seminorm.
Generalized metrics
Extending the range
Some authors allow the distance function d to attain the value ∞, i.e. distances are non-negative numbers on the extended real number line. Such a metric is called an extended metric. Every extended metric can be transformed to a finite metric such that the metric spaces are equivalent as far as notions of topology (such as continuity or convergence) are concerned. This can be done using a subadditive monotically increasing bounded function which is zero at zero, e.g. d'(x, y) = d(x, y) / (1 + d(x, y)) or d''(x, y) = min(1, d(x, y))).
The requirement that the metric take values in [0,∞) can even be relaxed to consider metrics with values in other directed sets. The reformulation of the axioms in this case leads to the construction of uniform spaces: topological spaces with an abstract structure enabling one to compare the local topologies of different points.
Relaxing the axioms
If the second requirement (indiscernibility) is relaxed to the condition d(x,x)=0 for all x, the function is called a pseudometric. This is the most common generalization of metrics. In topology, a semimetric is a function that satisfies the first three axioms, but not necessarily the triangle inequality. Occasionally, a quasimetric is defined as a function that satisfies all axioms for a metric with the possible exception of symmetry. Sometimes the presyllables are combined; the meaning is obvious. The pseduoquasimetric is sometimes called the hemimetric. Relaxing all three requirements leads to the prametric space.
These notions are not completely standardized. In particular, the term semimetric is often used as a synonym for pseudometric (especially in functional analysis).
The probability metric is an example of a pseudometric, i.e. a distance function that does not satisfy the identity of indiscernibles.
In inframetrics, the triangle inequality condition 4 is weakened.
Important cases of generalized metrics
From a categorical point of view, the extended pseudometric and the extended pseudoquasimetric spaces, along with their corresponding nonexpansive maps, are the best behaved of the metric space categories. One can take arbitrary products and coproducts and form quotient objects within the given category. If one drops "extended", one can only take finite products and coproducts. If one drops "pseudo", one cannot take quotients. Approach spaces are a generalization of metric spaces that maintains these good categorical properties.
In differential geometry, one considers metric tensors, which can be thought of as "infinitesimal" metric functions. They are defined as inner products on the tangent space with an appropriate differentiability requirement. While these are not metric functions as defined in this article, they induce metric functions by integration. A manifold with a metric tensor is called a Riemannian manifold. If one drops the positive definiteness requirement of inner product spaces, then one obtains a pseudo-Riemannian metric tensor, which integrates to a pseudo-semimetric. These are used in the geometric study of the theory of relativity, where the tensor is also called the "invariant distance".
See also
- Acoustic metric
- Complete metric