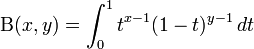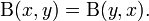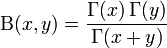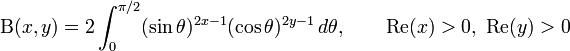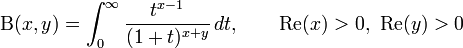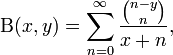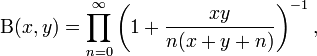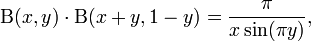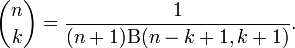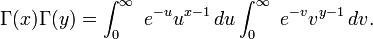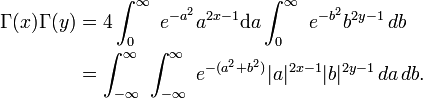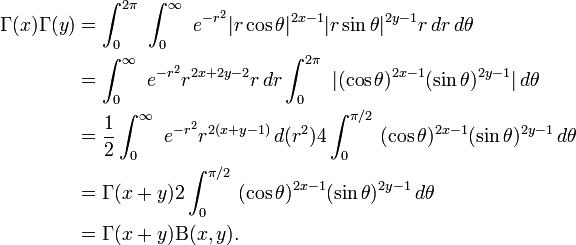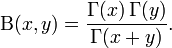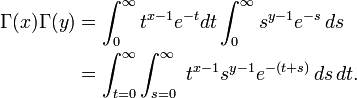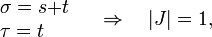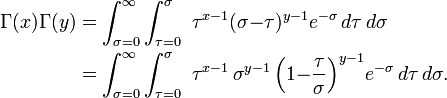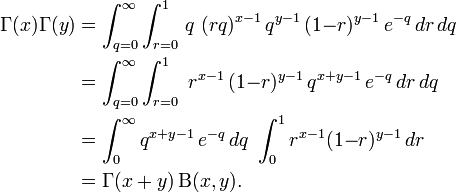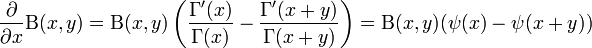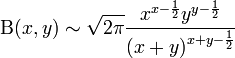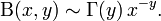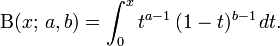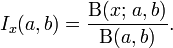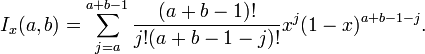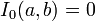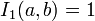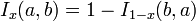Beta function
In mathematics, the beta function, also called the Euler integral of the first kind, is a special function defined by
for 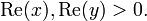
The beta function was studied by Euler and Legendre and was given its name by Jacques Binet.
Contents |
Properties
The beta function is symmetric, meaning that
It has many other forms, including:
where 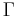 is the gamma function. The second identity shows in particular
is the gamma function. The second identity shows in particular 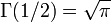 .
.
Just as the gamma function for integers describes factorials, the beta function can define a binomial coefficient after adjusting indices:
The beta function was the first known scattering amplitude in string theory, first conjectured by Gabriele Veneziano. It also occurs in the theory of the preferential attachment process, a type of stochastic urn process.
Relationship between Gamma function and Beta function
To derive the integral representation of the beta function, write the product of two factorials as
Now, let  ,
, 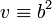 , so
, so
Transforming to polar coordinates with 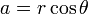 ,
, 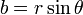 :
:
Hence, rewrite the arguments with the usual form of Beta function:
A somewhat more straightforward derivation:
The argument in the exponential inspires us to employ the substitution
where  is the Jacobian of the transformation. Using this transformation we arrive at:
is the Jacobian of the transformation. Using this transformation we arrive at:
Again, now the comparison to 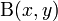 leads us to:
leads us to:
This leads to an easy identification with the expected result:
Derivatives
The derivatives follow:
where 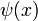 is the digamma function.
is the digamma function.
Integrals
The Nörlund-Rice integral is a contour integral involving the beta function.
Approximation
Stirling's approximation gives the asymptotic formula
for large x and large y. If on the other hand x is large and y is fixed, then
Incomplete beta function
The incomplete beta function is a generalization of the beta function that replaces the definite integral of the beta function with an indefinite integral. The situation is analogous to the incomplete gamma function being a generalization of the gamma function.
The incomplete beta function is defined as
For x = 1, the incomplete beta function coincides with the complete beta function.
The regularized incomplete beta function (or regularized beta function for short) is defined in terms of the incomplete beta function and the complete beta function:
Working out the integral (one can use integration by parts to do that) for integer values of a and b, one finds:
Properties
(Many other properties could be listed here.)
See also
- Beta distribution
- Binomial distribution
- Jacobi sum, the analogue of the beta function over finite fields.
- Negative binomial distribution
- Yule–Simon distribution
- Uniform distribution (continuous)
- superstrings
References
- Askey, R. A.; Roy, R. (2008), "Beta function", in Boisvert, Ronald F.; Clark, Charles W.; Lozier, Daniel M. et al., Digital Library of Mathematical Functions, N.I.S.T.
- M. Zelen and N. C. Severo. in Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See §6.2, 6.6, and 26.5)
- W. H. Press, B. P. Flannery, S. A. Teukolsky, W. T. Vetterling. Numerical Recipes in C. Cambridge, UK: Cambridge University Press, 1992. Second edition. (See section 6.4)
- Evaluation of beta function using Laplace transform on PlanetMath
- Arbitrarily accurate values can be obtained from The Wolfram Functions Site, Evaluate Beta Regularized Incomplete beta
External links
- Cephes - C and C++ language special functions math library
- Beta Function Calculator
- Incomplete Beta Function Calculator
- Regularized Incomplete Beta Function Calculator