Pythagoras
| Pythagoras Pre-Socratic philosophy |
|
 Bust of Pythagoras of Samos in the Capitoline Museums, Rome |
|
| Full name | Pythagoras (Πυθαγόρας) |
|---|---|
| Birth | c. 580 BC – 572 BC |
| Death | c. 500 BC – 490 BC |
| School/tradition | Pythagoreanism |
| Main interests | Metaphysics, Music, Mathematics, Ethics, Politics |
| Notable ideas | Musica universalis, Golden ratio, Pythagorean tuning, Pythagorean theorem |
|
Influenced by
|
|
|
Influenced
|
|
Pythagoras of Samos (Greek: Ὁ Πυθαγόρας ὁ Σάμιος, O Pūthagoras o Samios, "Pythagoras the Samian", or simply Ὁ Πυθαγόρας; born between 580 and 572 BC, died between 500 and 490 BC) was an Ionian Greek mathematician and founder of the religious movement called Pythagoreanism. He is often revered as a great mathematician, mystic and scientist; however some have questioned the scope of his contributions to mathematics and natural philosophy. Herodotus referred to him as "the most able philosopher among the Greeks". His name led him to be associated with Pythian Apollo; Aristippus explained his name by saying, "He spoke (agor-) the truth no less than did the Pythian (Pyth-)," and Iamblichus tells the story that the Pythia prophesied that his pregnant mother would give birth to a man supremely beautiful, wise, and beneficial to humankind.[1]
He is best known for the Pythagorean theorem, which bears his name. Known as "the father of numbers", Pythagoras made influential contributions to philosophy and religious teaching in the late 6th century BC. Because legend and obfuscation cloud his work even more than with the other pre-Socratics, one can say little with confidence about his life and teachings. We do know that Pythagoras and his students believed that everything was related to mathematics and that numbers were the ultimate reality and, through mathematics, everything could be predicted and measured in rhythmic patterns or cycles. According to Iamblichus, Pythagoras once said that "number is the ruler of forms and ideas and the cause of gods and demons."
He was the first man to call himself a philosopher, or lover of wisdom,[2] and Pythagorean ideas exercised a marked influence on Plato. Unfortunately, very little is known about Pythagoras because none of his writings have survived. Many of the accomplishments credited to Pythagoras may actually have been accomplishments of his colleagues and successors.
Contents |
Life
Pythagoras was born on Samos, a Greek island in the eastern Aegean, off the coast of Asia Minor. He was born to Pythais (his mother, a native of Samos) and Mnesarchus (his father, a Phoenician merchant from Tyre). As a young man, he left his native city for Croton, Calabria, in Southern Italy, to escape the tyrannical government of Polycrates. According to Iamblichus, Thales, impressed with his abilities, advised Pythagoras to head to Memphis in Egypt and study with the priests there who were renowned for their wisdom. He was also discipled in the temples of Tyre and Byblos in Phoenicia. It may have been in Egypt where he learned some geometric principles which eventually inspired his formulation of the theorem that is now called by his name. This possible inspiration is presented as an extraordinaire problem in the Berlin Papyrus. Upon his migration from Samos to Croton, Calabria, Italy, Pythagoras established a secret religious society very similar to (and possibly influenced by) the earlier Orphic cult.

Pythagoras undertook a reform of the cultural life of Croton, urging the citizens to follow virtue and form an elite circle of followers around himself called Pythagoreans. Very strict rules of conduct governed this cultural center. He opened his school to both male and female students uniformly. Those who joined the inner circle of Pythagoras's society called themselves the Mathematikoi. They lived at the school, owned no personal possessions and were required to assume a mainly vegetarian diet (meat that could be sacrificed was allowed to be eaten). Other students who lived in neighboring areas were also permitted to attend Pythagoras's school. Known as Akousmatikoi, these students were permitted to eat meat and own personal belongings. Richard Blackmore, in his book The Lay Monastery (1714), saw in the religious observances of the Pythagoreans, "the first instance recorded in history of a monastic life."
According to Iamblichus, the Pythagoreans followed a structured life of religious teaching, common meals, exercise, reading and philosophical study. Music featured as an essential organizing factor of this life: the disciples would sing hymns to Apollo together regularly; they used the lyre to cure illness of the soul or body; poetry recitations occurred before and after sleep to aid the memory.
Flavius Josephus, in his polemical Against Apion, in defence of Judaism against Greek philosophy, mentions that according to Hermippus of Smyrna, Pythagoras was familiar with Jewish beliefs, incorporating some of them in his own philosophy.
Towards the end of his life he fled to Metapontum because of a plot against him and his followers by a noble of Croton named Cylon. He died in Metapontum around 90 years old from unknown causes.
Bertrand Russell, in A History of Western Philosophy, contended that the influence of Pythagoras on Plato and others was so great that he should be considered the most influential of all western philosophers.
Pythagoreans

The organization was in some ways a school, in some ways a brotherhood, and in some ways a monastery. It was based upon the religious teachings of Pythagoras and was very secretive. At first, the school was highly concerned with the morality of society. Members were required to live ethically, love one another, share political beliefs, practice pacifism, and devote themselves to the mathematics of nature.
Pythagoras's followers were commonly called "Pythagoreans". They are generally accepted as philosophical mathematicians who had an influence on the beginning of axiomatic geometry, which after two hundred years of development was written down by Euclid in The Elements.
The Pythagoreans observed a rule of silence called echemythia, the breaking of which was punishable by death. This was because the Pythagoreans believed that a man's words were usually careless and misrepresented him and that when someone was "in doubt as to what he should say, he should always remain silent". Another rule that they had was to help a man "in raising a burden, but do not assist him in laying it down, for it is a great sin to encourage indolence", and they said "departing from your house, turn not back, for the furies will be your attendants"; this axiom reminded them that it was better to learn none of the truth about mathematics, God, and the universe at all than to learn a little without learning all. (The Secret Teachings of All Ages by Manly P. Hall).
In his biography of Pythagoras (written seven centuries after Pythagoras's time), Porphyry stated that this silence was "of no ordinary kind." The Pythagoreans were divided into an inner circle called the mathematikoi ("mathematicians") and an outer circle called the akousmatikoi ("listeners"). Porphyry wrote "the mathematikoi learned the more detailed and exactly elaborated version of this knowledge, the akousmatikoi (were) those who had heard only the summary headings of his (Pythagoras's) writings, without the more exact exposition." According to Iamblichus, the akousmatikoi were the exoteric disciples who listened to lectures that Pythagoras gave out loud from behind a veil.
The akousmatikoi were not allowed to see Pythagoras and they were not taught the inner secrets of the cult. Instead they were taught laws of behavior and morality in the form of cryptic, brief sayings that had hidden meanings. The akousmatikoi recognized the mathematikoi as real Pythagoreans, but not vice versa. After the murder of a number of the mathematikoi by the cohorts of Cylon, a resentful disciple, the two groups split from each other entirely, with Pythagoras's wife Theano and their two daughters leading the mathematikoi.
Theano, daughter of the Orphic initiate Brontinus, was a mathematician in her own right. She is credited with having written treatises on mathematics, physics, medicine, and child psychology, although nothing of her writing survives. Her most important work is said to have been a treatise on the principle of the golden mean. In a time when women were usually considered property and relegated to the role of housekeeper or spouse, Pythagoras allowed women to function on equal terms in his society.
The Pythagorean society is associated with prohibitions such as not to step over a crossbar, and not to eat beans. These rules seem like primitive superstition, similar to "walking under a ladder brings bad luck". The abusive epithet mystikos logos ("mystical speech") was hurled at Pythagoras even in ancient times to discredit him. The prohibition on beans could be linked to favism, which is relatively widespread around the Mediterranean.
The key here is that akousmata means "rules", so that the superstitious taboos primarily applied to the akousmatikoi, and many of the rules were probably invented after Pythagoras's death and independent from the mathematikoi (arguably the real preservers of the Pythagorean tradition). The mathematikoi placed greater emphasis on inner understanding than did the akousmatikoi, even to the extent of dispensing with certain rules and ritual practices. For the mathematikoi, being a Pythagorean was a question of innate quality and inner understanding.
There was also another way of dealing with the akousmata — by allegorizing them. We have a few examples of this, one being Aristotle's explanations of them: "'step not over a balance', i.e. be not covetous; 'poke not the fire with a sword', i.e. do not vex with sharp words a man swollen with anger, 'eat not heart', i.e. do not vex yourself with grief," etc. We have evidence for Pythagoreans allegorizing in this way at least as far back as the early fifth century BC. This suggests that the strange sayings were riddles for the initiated.
The Pythagoreans are known for their theory of the transmigration of souls, and also for their theory that numbers constitute the true nature of things. They performed purification rites and followed and developed various rules of living which they believed would enable their soul to achieve a higher rank among the gods.
Much of their mysticism concerning the soul seem inseparable from the Orphic tradition. The Orphics advocated various purificatory rites and practices as well as incubatory rites of descent into the underworld. Pythagoras is also closely linked with Pherecydes of Syros, the man ancient commentators tend to credit as the first Greek to teach a transmigration of souls. Ancient commentators agree that Pherekydes was Pythagoras's most intimate teacher. Pherekydes expounded his teaching on the soul in terms of a pentemychos ("five-nooks", or "five hidden cavities") — the most likely origin of the Pythagorean use of the pentagram, used by them as a symbol of recognition among members and as a symbol of inner health (ugieia).
Musical theories and investigations
Pythagoras was very interested in music, and so were his followers. The Pythagoreans were musicians as well as mathematicians. Pythagoras wanted to improve the music of his day, which he believed was not harmonious enough and was too hectic.
According to legend, the way Pythagoras discovered that musical notes could be translated into mathematical equations was when one day he passed blacksmiths at work, and thought that the sounds emanating from their anvils being hit were beautiful and harmonious and decided that whatever scientific law caused this to happen must be mathematical and could be applied to music. He went to the blacksmiths to learn how this had happened by looking at their tools, he discovered that it was because the anvils were "simple ratios of each other, one was half the size of the first, another was 2/3 the size, and so on." (See Pythagorean tuning.)
The Pythagoreans elaborated on a theory of numbers, the exact meaning of which is still debated among scholars. Pythagoras believed in something called the "harmony of the spheres." He believed that the planets and stars moved according to mathematical equations, which corresponded to musical notes and thus produced a symphony.[3]
| Academic Genealogy | |
|---|---|
| Notable teachers | Notable students |
| Anaximander Pherecydes of Syros |
Ameinias Bathyllus |
Influence

Since the fourth century AD, Pythagoras has commonly been given credit for discovering the Pythagorean theorem, a theorem in geometry that states that in a right-angled triangle the square of the hypotenuse (the side opposite the right angle), c, is equal to the sum of the squares of the other two sides, b and a—that is, a² + b² = c².
While the theorem that now bears his name was known and previously utilized by the Babylonians and Indians, he, or his students, are often said to have constructed the first proof. It must, however, be stressed that the way in which the Babylonians handled Pythagorean numbers, implies that they knew that the principle was generally applicable, and knew some kind of proof, which has not yet been found in the (still largely unpublished) cuneiform sources.[4] Because of the secretive nature of his school and the custom of its students to attribute everything to their teacher, there is no evidence that Pythagoras himself worked on or proved this theorem. For that matter, there is no evidence that he worked on any mathematical or meta-mathematical problems. Some attribute it as a carefully constructed myth by followers of Plato over two centuries after the death of Pythagoras, mainly to bolster the case for Platonic meta-physics, which resonate well with the ideas they attributed to Pythagoras. This attribution has stuck, down the centuries up to modern times.[5] The earliest known mention of Pythagoras's name in connection with the theorem occurred five centuries after his death, in the writings of Cicero and Plutarch.
Today, Pythagoras is revered as a prophet by the Ahl al-Tawhid or Druze faith along with his fellow Greek, Plato. But Pythagoras also had his critics, such as Heraclitus who said that "much learning does not teach wisdom; otherwise it would have taught Hesiod and Pythagoras, and again Xenophanes and Hecataeus".[6]
Religion and science
Pythagoras’ religious and scientific views were, in his opinion, inseparably interconnected. However, they are looked at separately in the 21st century. Religiously, Pythagoras was a believer of metempsychosis. He believed in transmigration, or the reincarnation of the soul again and again into the bodies of humans, animals, or vegetables until it became moral. His ideas of reincarnation were influenced by ancient Greek religion. He was one of the first to propose that the thought processes and the soul were located in the brain and not the heart. He himself claimed to have lived four lives that he could remember in detail, and heard the cry of his dead friend in the bark of a dog.
One of Pythagoras' beliefs was that the essence of being is number. Thus, being relies on stability of all things that create the universe. Things like health relied on a stable proportion of elements; too much or too little of one thing causes an imbalance that makes a being unhealthy. Pythagoras viewed thinking as the calculating with the idea numbers. When combined with the Folk theories, the philosophy evolves into a belief that Knowledge of the essence of being can be found in the form of numbers. If this is taken a step further, one can say that because mathematics is an unseen essence, the essence of being is an unseen characteristic that can be encountered by the study of mathematics.
Literary works
No texts by Pythagoras survive, although forgeries under his name — a few of which remain extant — did circulate in antiquity. Critical ancient sources like Aristotle and Aristoxenus cast doubt on these writings. Ancient Pythagoreans usually quoted their master's doctrines with the phrase autos ephe ("he himself said") — emphasizing the essentially oral nature of his teaching. Pythagoras appears as a character in the last book of Ovid's Metamorphoses, where Ovid has him expound upon his philosophical viewpoints. Pythagoras has been quoted as saying, "No man is free who cannot command himself."
Lore
There is another side to Pythagoras, as he became the subject of elaborate legends surrounding his historic persona. Aristotle described Pythagoras as wonder-worker and somewhat of a supernatural figure, attributing to him such aspects as a golden thigh, which was a sign of divinity. According to Aristotle and others' accounts, some ancients believed that he had the ability to travel through space and time, and to communicate with animals and plants.[7] An extract from Brewer's Dictionary of Phrase and Fable's entry entitled "Golden Thigh":
Pythagoras is said to have had a golden thigh, which he showed to Abaris, the Hyperborean priest, and exhibited in the Olympic games.[8]
Another legend, also taken from Brewer's Dictionary, describes his writing on the moon:
Pythagoras asserted he could write on the moon. His plan of operation was to write on a looking-glass in blood, and place it opposite the moon, when the inscription would appear photographed or reflected on the moon's disc.[9]
Other accomplishments

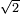 is irrational.
is irrational.One of Pythagoras's major accomplishments was the discovery that music was based on proportional intervals of the numbers one through four. He believed that the number system, and therefore the universe system, was based on the sum of these numbers: ten. Pythagoreans swore by the Tetrachtys of the Decad, or ten, rather than by the gods. Odd numbers were masculine and even were feminine. He discovered the theory of mathematical proportions, constructed from three to five geometrical solids. One of his order, Hippasos, also discovered irrational numbers, but the idea was unthinkable to Pythagoras, and according to one version this member was executed. Pythagoras (or the Pythagoreans) also discovered square numbers. They found that if one took, for example, four small stones and arranged them into a square, each side of the square was not only equivalent to the other, but that when the two sides were multiplied together, they equaled the sum total of stones in the square arrangement, hence the name "Square Root"[10]. He was one of the first to think that the earth was round, that all planets have an axis, and that all the planets travel around one central point. He originally identified that point as Earth, but later renounced it for the idea that the planets revolve around a central “fire” that he never identified as the sun. He also believed that the moon was another planet that he called a “counter-Earth” – furthering his belief in the Limited-Unlimited.
Groups influenced by Pythagoras
Influence on Plato
Pythagoras or in a broader sense, the Pythagoreans, allegedly exercised an important influence on the work of Plato. According to R. M. Hare, his influence consists of three points: a) the platonic Republic might be related to the idea of "a tightly organized community of like-minded thinkers", like the one established by Pythagoras in Croton. b) there is evidence that Plato possibly took from Pythagoras the idea that mathematics and, generally speaking, abstract thinking is a secure basis for philosophical thinking as well as "for substantial theses in science and morals". c) Plato and Pythagoras shared a "mystical approach to the soul and its place in the material world". It is probable that both have been influenced by Orphism.[11]
Plato's harmonics were clearly influenced by the work of Archytas, a genuine Pythagorean of the third generation, who made important contributions to geometry, reflected in Book VIII of Euclid's Elements.
Roman influence
In the legends of ancient Rome, Numa Pompilius, the second King of Rome, is said to have studied under Pythagoras. This is unlikely, since the commonly accepted dates for the two lives do not overlap.
Influence on esoteric groups
Pythagoras started a secret society called the Pythagorean brotherhood devoted to the study of mathematics. This had a great effect on future esoteric traditions, such as Rosicrucianism and Freemasonry, both of which were occult groups dedicated to the study of mathematics and both of which claimed to have evolved out of the Pythagorean brotherhood. The mystical and occult qualities of Pythagorean mathematics are discussed in a chapter of Manly P. Hall's The Secret Teachings of All Ages entitled "Pythagorean Mathematics".
Pythagorean theory was tremendously influential on later numerology, which was extremely popular throughout the Middle East in the ancient world. The 8th-century Muslim alchemist Jabir ibn Hayyan grounded his work in an elaborate numerology greatly influenced by Pythagorean theory.
See also
|
|
Notes
- ↑ Riedweg, Christoph (2005). Pythagoras: His Life, Teaching and Influence. Cornell University. pp. 5–6, 59, 73.
- ↑ Cicero, Tusculan Disputations, 5.3.8-9 = Heraclides Ponticus fr. 88 Wehrli, Diogenes Laertius 1.12, 8.8, Iamblichus VP 58. Burkert attempted to discredit this ancient tradition, but it has been defended by C.J. De Vogel, Pythagoras and Early Pythagoreanism (1966), pp. 97-102, and C. Riedweg, Pythagoras: His Life, Teaching, And Influence (2005), p. 92.
- ↑ Christoph Riedweg, Pythagoras: His Life, Teaching and Influence, Cornell: Cornell University Press, 2005 .
- ↑ There are about 100,000 unpublished cuneiform sources in the British Museum alone. Babylonian knowledge of proof of the Pythagorean Theorem is discussed by J. Høyrup, 'The Pythagorean "Rule" and "Theorem" - Mirror of the Relation between Babylonian and Greek Mathematics,' in: J. Renger (red.): Babylon. Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne (1999).
- ↑ From Christoph Riedweg , Pythagoras, His Life, Teaching and Influence, Cornell: Cornell University Press, 2005: "Had Pythagoras and his teachings not been since the early Academy overwritten with Plato’s philosophy, and had this ‘palimpsest’ not in the course of the Roman Empire achieved unchallenged authority among Platonists, it would be scarcely conceivable that scholars from the Middle Ages and modernity down to the present would have found the Presocratic charismatic from Samos so fascinating. In fact, as a rule it was the image of Pythagoras elaborated by Neopythagoreans and Neoplatonists that determined the idea of what was Pythagorean over the centuries."
- ↑ Diog. L. ix. 1 (Fr. 40 in Vorsokratiker, i3, p. 86. 1-3)
- ↑ Huffman, Carl. Pythagoras (Stanford Encyclopedia of Philosophy) [1]
- ↑ Brewer, E. Cobham, Brewer's Dictionary of Phrase and Fable [2]
- ↑ Brewer, E. Cobham, Brewer's Dictionary of Phrase and Fable [3]
- ↑ Alioto, Anthony. A History of Western Science- 2nd ed. New York:Prentice Hall, 1992. p. 39-42
- ↑ R.M. Hare, Plato in C.C.W. Taylor, R.M. Hare and Jonathan Barnes, Greek Philosophers, Socrates, Plato, and Aristotle, Oxford: Oxford University Press, 1999 (1982), 103-189, here 117-9.
References
Primary sources
No primary sources about Pythagoras have survived. This article describes the classical interpretation of Pythagoras, which is based on a small set of texts written between 150 AD and 450 AD. As these texts were written 600 to 1000 years after Pythagoras is said to have lived, their accuracy is uncertain.
It is postulated that the classical Pythagoras did not exist prior to these biographies: many of the discoveries and life details they attributed to Pythagoras may have been those of other Pythagoreans, if not fiction. This would explain the lack of reference to a man Pythagoras until 150 AD, given that he would have been of interest to contemporary philosophers (Aristotle referred to the so-called Pythagoreans). It is suggested that the mathematical significance of the early Pythagoreans (pre 450 BC) has been exaggerated (with the exception of their theory of harmonics), and that the Pythagoreans were an Orphic-like cult with an emphasis on numerology who only later evolved into serious mathematicians as geometry became popular across Greece.
The so-called Pythagoreans, who were the first to take up mathematics, not only advanced this subject, but saturated with it, they fancied that the principles of mathematics were the principles of all things.
—Aristotle, Metaphysics 1-5 , cc. 350 BC
Classical secondary sources
Only a few relevant source texts deal with Pythagoras and the Pythagoreans, most are available in different translations. Other texts usually build solely on information in these works.
- Diogenes Laertius, Vitae philosophorum VIII (Lives of Eminent Philosophers), c. 200 AD, which in turn reference the lost work Successions of Philosophers by Alexander Polyhistor) — Pythagoras, Translation by C.D. Yonge
- Porphyry, Vita Pythagorae (Life of Pythagoras), c. 270 AD
- Iamblichus, De Vita Pythagorica (On the Pythagorean Life), c. 300 AD
- Apuleius also writes about Pythagoras in Apologia, including a story of him being taught by Babylonian disciples of Zoroaster, c. 150 AD
- Hierocles of Alexandria, Golden Verses of Pythagoras, Concord Grove Pr., 1983 c.430 AD
Modern secondary sources
- Burkert, Walter. Lore and Science in Ancient Pythagoreanism. Harvard University Press, June 1, 1972. ISBN 0-674-53918-4
- Burnyeat, M. F. "The Truth about Pythagoras". London Review of Books, 22 February 2007.
- Guthrie, W. K. A History of Greek Philosophy: Earlier Presocratics and the Pythagoreans, Cambridge University Press, 1979. ISBN 0-521-29420-7
- Kingsley, Peter. Ancient Philosophy, Mystery, and Magic: Empedocles and the Pythagorean Tradition. Oxford University Press, 1995.
- Hermann, Arnold. To Think Like God: Pythagoras and Parmenides—the Origins of Philosophy. Parmenides Publishing, 2005. ISBN 978-1-930972-00-1
- O'Meara, Dominic J. Pythagoras Revived. Oxford University Press, 1989. ISBN 0-19-823913-0 (paperback), ISBN 0-19-824485-1 (hardcover)
External links
- “Other Lives” by M.F. Burnyeat, an article about current Pythagoras scholarship
- Pythagoreanism Web Site
- References for Pythagoras
- Pythagoras, Internet Encyclopedia of Philosophy
- Pythagoras of Samos, The MacTutor History of Mathematics archive, School of Mathematics and Statistics, University of St Andrews, Scotland
- Pythagoras and the Pythagoreans, Fragments and Commentary, Arthur Fairbanks Hanover Historical Texts Project, Hanover College Department of History
- Pythagoras and the Pythagoreans, Department of Mathematics, Texas A&M University
- Pythagoras and Pythagoreanism, The Catholic Encyclopedia
- Pythagoreanism Web Article
- Occult conception of Pythagoreanism
- Pythagoras of Samos
- Stanford Encyclopedia of Philosophy entry
- Tetraktys
- Golden Verses of Pythagoras
- Pythagoras on Vegetarianism Quotes from primary source historical literature on Pythagoras' view on Vegetarianism, Justice and Kindness
- Wandering Souls: The Doctrine of Transmigration in Pythagorean Philosophy, by Dr. James Luchte
- http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Pythagoras.html
|
|||||||||||||||||||||||
|
|||||
|
|||||||||||||||||||||||||||||||
| Persondata | |
|---|---|
| NAME | Pythagoras |
| ALTERNATIVE NAMES | Πυθαγόρας (Greek) |
| SHORT DESCRIPTION | Ionian philosopher |
| DATE OF BIRTH | circa 580 BC |
| PLACE OF BIRTH | Samos Island |
| DATE OF DEATH | circa 500 BC |
| PLACE OF DEATH | |