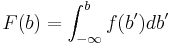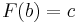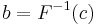Pseudorandom number generator
A pseudorandom number generator (PRNG) is an algorithm for generating a sequence of numbers that approximates the properties of random numbers. The sequence is not truly random in that it is completely determined by a relatively small set of initial values, called the PRNG's state. Although sequences that are closer to truly random can be generated using hardware random number generators, pseudo-random numbers are important in practice for simulations (e.g., of physical systems with the Monte Carlo method), and are central in the practice of cryptography.
Most pseudo-random generator algorithms produce sequences which are uniformly distributed by any of several tests. Common classes of these algorithms are linear congruential generators, lagged Fibonacci generators, linear feedback shift registers and generalised feedback shift registers. Recent instances of pseudo-random algorithms include Blum Blum Shub, Fortuna, and the Mersenne twister.
Careful mathematical analysis is required to have any confidence a PRNG generates numbers that are sufficiently "random" to suit the intended use. Robert R. Coveyou of Oak Ridge National Laboratory once titled an article, "The generation of random numbers is too important to be left to chance."[1] As John von Neumann joked, "Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin."[2]
Contents |
Periodicity
A PRNG can be started from an arbitrary starting state, using a seed state. It will always produce the same sequence thereafter when initialized with that state. The maximum length of the sequence before it begins to repeat is determined by the size of the state, measured in bits. However, since the length of the maximum period potentially doubles with each bit of 'state' added, it is easy to build PRNGs with periods long enough for any practical application.
If a PRNG's internal state contains n bits, its period can be no longer than 2n results. For some PRNGs the period length can be calculated without walking through the whole period. Linear Feedback Shift Registers (LFSRs) are usually chosen to have periods of exactly 2n-1. Linear congruential generators have periods that can be calculated by factoring. Mixes (no restrictions) have periods of about 2n/2 on average, usually after walking through a nonrepeating starting sequence. Mixes that are reversible (permutations) have periods of about 2n-1 on average, and the period will always include the original internal state (e.g. [1]). Although PRNGs will repeat their results after they reach the end of their period, a repeated result does not imply that the end of the period has been reached.
It is an open question, and one central to the theory and practice of cryptography, whether there is any way to distinguish the output of a high-quality PRNG from a truly random sequence without knowing the algorithm(s) used and the state with which it was initialized. The security of most cryptographic algorithms and protocols using PRNGs is based on the assumption that it is infeasible to distinguish use of a suitable PRNG from a random sequence. The simplest examples of this dependency are stream ciphers, which (most often) work by exclusive oring the plaintext of a message with the output of a PRNG, producing ciphertext. The design of cryptographically adequate PRNGs is extremely difficult.
Problems with deterministic generators
In practice, the output from many common PRNGs exhibit artifacts which cause them to fail statistical pattern detection tests. These include, but are certainly not limited to
- Shorter than expected periods for some seed states; such seed states may be called 'weak' in this context
- Lack of uniformity of distribution
- Correlation of successive values
- Poor dimensional distribution of the output sequence
- The distances between where certain values occur are distributed differently from those in a random sequence distribution
Defects exhibited by flawed PRNGs range from unnoticeable to absurdly obvious. The RANDU random number algorithm used for decades on mainframe computers was seriously flawed, and much research work of that period is less reliable than it might have been as a result.
Early approaches
An early computer-based PRNG, suggested by John von Neumann in 1946, is known as the middle-square method. It is very simple: take any number, square it, remove the middle digits of the resulting number as your "random number", then use that number as the seed for the next iteration. For example, squaring the number "1111" yields "1234321", which can be written as "01234321", an 8-digit number being the square of a 4-digit number. This gives "2343" as the "random" number. Repeating this procedure gives "4896" as the next result, and so on. Von Neumann used 10 digit numbers, but the process was the same.
A problem with the "middle square" method is that all sequences eventually repeat themselves, some very quickly, such as "0000". Von Neumann was aware of this, but he found the approach sufficient for his purposes, and was worried that mathematical "fixes" would simply hide errors rather than remove them.
Von Neumann judged hardware random number generators unsuitable, for, if they did not record the output generated, they could not later be tested for errors. If they did record their output, they would exhaust the limited computer memories available then, and so the computer's ability to read and write numbers. If the numbers were written to cards, they would take very much longer to write and read. On the ENIAC computer he was using, the "middle square" method generated numbers at a rate some two hundred times faster than reading numbers in from punch cards.
The middle-square method has been supplanted by more elaborate generators.
Mersenne twister
The 1997 invention of the Mersenne twister algorithm, by Makoto Matsumoto and Takuji Nishimura, avoids many of the problems with earlier generators. It has the colossal period of 219937-1 iterations (>43×106000), is proven to be equidistributed in (up to) 623 dimensions (for 32-bit values), and runs faster than other statistically reasonable generators. It is now increasingly becoming the random number generator of choice for statistical simulations and generative modeling. SFMT, SIMD-oriented Fast Mersenne Twister, a variant of Mersenne twister, is faster even if it's not compiled with SIMD support.[2]
Although suitable for other purposes, the Mersenne twister is not considered suitable for use in cryptography. A variant has been proposed as a cryptographic cipher. [3]
Cryptographically secure pseudorandom number generators
A PRNG suitable for cryptographic applications is called a cryptographically secure PRNG (CSPRNG). The difference between a PRNG and a CSPRNG is not simple: a CSPRNG must meet certain design principles and be resistant to known attacks. Years of review are required before such an algorithm can be certified and it is still possible attacks will be discovered in the future.
Some classes of CSPRNGs include the following:
- Stream ciphers
- block ciphers running in counter or output feedback mode.
- Special designs with a security proof. For example Blum Blum Shub has a strong security proof, although the proof is conditional and requires that some internal values remain secret from any attacker. Moreover, Blum Blum Shub is too slow for many applications.
- PRNGs that have been designed specifically to be cryptographically secure, such as Microsoft's Cryptographic Application Programming Interface function CryptGenRandom, the Yarrow algorithm (incorporated in Mac OS X and FreeBSD), and Fortuna.
- Combination PRNGs which attempt to combine several PRNG primitive algorithms with the goal of removing any non-randomness.
BSI evaluation criteria
The German Federal Office for Information Security (BSI) has established four criteria for quality of deterministic random number generators. They are summarized here:
- K1 -- A sequence of random numbers with a high probability of containing no identical consecutive elements.
- K2 -- A sequence of numbers which is indistinguishable from 'true random' numbers according to specified statistical tests. The tests are the monobit test (equal numbers of ones and zeros in the sequence), poker test (a special instance of the chi-square test), runs test (counts the frequency of runs of various lengths), longruns test (checks whether there exists any run of length 34 or greater in 20 000 bits of the sequence) -- both from BSI2 (AIS 20, v. 1, 1999) and FIPS (140-1, 1994), and the autocorrelation test. In essence, these requirements are a test of how well a bit sequence: has zeros and ones equally often; after a sequence of n zeros (or ones), the next bit a one (or zero) with probability one-half; and any selected subsequence contains no information about the next element(s) in the sequence.
- K3 -- It should be impossible for any attacker (for all practical purposes) to calculate, or otherwise guess, from any given sub-sequence, any previous or future values in the sequence, nor any inner state of the generator.
- K4 -- It should be impossible, for all practical purposes, for an attacker to calculate, or guess from an inner state of the generator, any previous numbers in the sequence or any previous inner generator states.
For cryptographic applications, only generators meeting the K4 standard are really acceptable.
Non-uniform generators
Numbers selected from a non-uniform probability distribution can be generated using a uniform distribution PRNG and a function that relates the two distributions.
First, one needs the cumulative distribution function 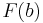 of the target distribution
of the target distribution 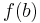 :
:
Note that 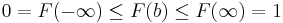 . Using a random number from a uniform distribution c as the probability density to "pass by", we get
. Using a random number from a uniform distribution c as the probability density to "pass by", we get
so that
is a number randomly selected from distribution 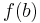 .
.
For example the inverse of cumulative Gaussian distribution 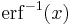 with an ideal uniform PRNG with range (0, 1) as input
with an ideal uniform PRNG with range (0, 1) as input 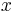 would produce a sequence of (positive only) values with a Gaussian distribution; however
would produce a sequence of (positive only) values with a Gaussian distribution; however
- when using practical number representations the infinite "tails" of the distribution have to be truncated to finite values.
- Repetitive recalculation of
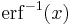 should be reduced by means such as ziggurat algorithm for faster generation.
should be reduced by means such as ziggurat algorithm for faster generation.
Similar considerations apply to generating other non-uniform distributions such as Rayleigh and Poisson.
See also
- Monte Carlo method
- Pseudorandom binary sequence
- Randomized algorithm
- Random number generator
- Random number generator attack
- List of pseudorandom number generators
- Randomness
Notes
- ↑ Peterson, Ivars. The Jungles of Randomness: A Mathematical Safari. Wiley, NY, 1998. (pp. 178) ISBN 0-471-16449-6
- ↑ "Various techniques used in connection with random digits", Applied Mathematics Series, no. 12, 36-38 (1951).
References
- Michael Luby, Pseudorandomness and Cryptographic Applications, Princeton Univ Press, 1996. A definitive source of techniques for provably random sequences.
- Donald Knuth. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89684-2. Chapter 3, pp.1–193. Extensive coverage of statistical tests for non-randomness.
- R. Matthews Maximally Periodic Reciprocals Bulletin of the Institute of Mathematics and its Applications 28 147-148 1992
- J. Viega, Practical Random Number Generation in Software, in Proc. 19th Annual Computer Security Applications Conference, Dec. 2003.
- John von Neumann, "Various techniques used in connection with random digits," in A.S. Householder, G.E. Forsythe, and H.H. Germond, eds., Monte Carlo Method, National Bureau of Standards Applied Mathematics Series, 12 (Washington, D.C.: U.S. Government Printing Office, 1951): 36-38.
- NIST Recommendation for Random Number Generation Using Deterministic Random Bit Generators
- Luc Devroye Non-Uniform Random Variate Generation, Springer-Verlag, New York, 1986.
External links
- The GNU Scientific Library. A free (GPL) C library that includes a number of PRNG algorithms.
- DieHarder: A free (GPL) C Random Number Test Suite.
- crng: Random-number generators (RNGs) implemented as Python extension types coded in C.
- http://eeyore.wu-wien.ac.at/src/ prng: A collection of algorithms for generating pseudorandom numbers as a library of C functions, released under the GPL.
- Strange Attractors and TCP/IP Sequence Number Analysis - an analysis of the strength of PRNGs used to create TCP/IP sequence numbers by various operating systems using strange attractors. This is a good practical example of issues in PRNGs and the variation possible in their implementation.
- Strange Attractors and TCP/IP Sequence Number Analysis - One Year Later - a follow-up article demonstrating some of the evolution of various PRNG algorithms over time.
- Generating random numbers Generating random numbers in Embedded Systems by Eric Uner
- Analysis of the Linux Random Number Generator by Zvi Gutterman, Benny Pinkas, and Tzachy Reinman