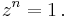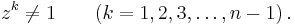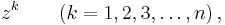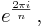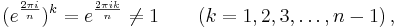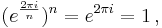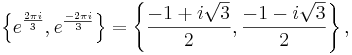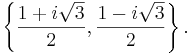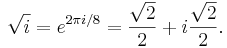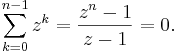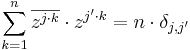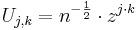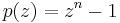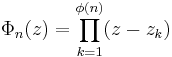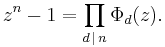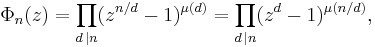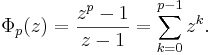Root of unity
In mathematics, the nth roots of unity, or de Moivre numbers, are all the complex numbers that yield 1 when raised to a given power n. They are located on the unit circle of the complex plane, and in that plane they form the vertices of an n-sided regular polygon with one vertex on 1.
Contents |
Definition



An nth root of unity, where n = 1,2,3,···, is a complex number, z, satisfying the equation
Second roots are called square roots, and third roots are called cube roots.
An nth root of unity is primitive if
There are n different nth roots of unity:
where z is any primitive nth root of unity. The primitive nth roots of unity are those zk where k and n are coprime.
Examples
One primitive nth root of unity is
because
and
- see exponentiation and Euler's identity.
The number (+1) is a square root of unity because (+1)2 = 1, but it is not a primitive square root of unity because (+1)1 = 1. So (+1) is only a primitive first root of unity. The number (−1) is a primitive square root of unity because (−1)1 ≠ 1 and (−1)2 = 1. For n>2, the primitive nth roots of unity are non-real complex numbers.
The two primitive cube roots of unity are
where 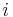 is the imaginary unit.
is the imaginary unit.
The two primitive fourth roots of unity are
The four primitive fifth roots of unity are
The two primitive sixth roots of unity are
A primitive eighth root of unity is
See heptadecagon for the real part of a seventeenth root of unity.
Periodicity
If z is a primitive nth root of unity, then the sequence of powers
- ··· , z−1, z0, z1, ···
is n-periodic, (because z j+n = z j·zn = z j·1 = z j for all values of j,) and the n sequences of powers
- ··· , z k·(−1), z k·0, zk·1, ··· (for k = 1···n),
are all n-periodic. These n sequences have furthermore the property of linear independence. This means that any n-periodic sequence of complex numbers
- ··· , x−1 , x0 , x1 , ···
can be expressed as a linear combination of powers of a primitive nth root of unity:
- x j = Σk Xk·zk·j = X1·z1·j + ··· + Xn·zn·j .
This is a form of Fourier analysis. If j is a (discrete) time variable, then k is a frequency and Xk is a complex amplitude.
Choosing for the primitive nth root of unity
- z = ei·2·π/n = cos(2·π/n) + i·sin(2·π/n)
allows x j to be expressed as a linear combination of cos and sin
- x j = Σk Ak·cos(2·π·j·k/n) + Σk Bk·sin(2·π·j·k/n).
This is a discrete Fourier transform.
Summation
The nth roots of unity add up according to the formula for a geometric series. (This summation is a special case of the Gaussian sum.) For n > 1:
where z is a primitive nth root of unity. For n = 1, the sum has only one term: z0=1.
Orthogonality
From the summation formula follows an orthogonality relationship: for j = 1, ···, n and j ' = 1, ···, n
where 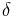 is the Kronecker delta and z is any primitive nth root of unity.
is the Kronecker delta and z is any primitive nth root of unity.
The 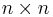 matrix
matrix 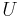 whose
whose  th entry is
th entry is
defines a discrete Fourier transform. Computing the inverse transformation using gaussian elimination requires O(n3) operations. However, it follows from the orthogonality that U is unitary. That is,
and thus the inverse of U is simply the complex conjugate. (This fact was first noted by Gauss when solving the problem of trigonometric interpolation). The straightforward application of U or its inverse to a given vector requires O(n2) operations. The fast Fourier transform algorithms reduces the number of operations further to O(n log n).
Cyclotomic polynomials
The zeroes of the polynomial
are precisely the nth roots of unity, each with multiplicity 1.
The nth cyclotomic polynomial is defined by the fact that its zeros are precisely the primitive nth roots of unity, each with multiplicity 1:
where z1,...,zφ(n) are the primitive nth roots of unity, and 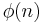 is Euler's totient function. The polynomial
is Euler's totient function. The polynomial 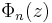 has integer coefficients and is an irreducible polynomial over the rational numbers (i.e., it cannot be written as the product of two positive-degree polynomials with rational coefficients). The case of prime n, which is easier than the general assertion, follows by applying Eisenstein's criterion to the polynomial
has integer coefficients and is an irreducible polynomial over the rational numbers (i.e., it cannot be written as the product of two positive-degree polynomials with rational coefficients). The case of prime n, which is easier than the general assertion, follows by applying Eisenstein's criterion to the polynomial 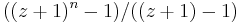 , and expanding via the binomial theorem.
, and expanding via the binomial theorem.
Every nth root of unity is a primitive dth root of unity for exactly one positive divisor d of n. This implies that
This formula represents the factorization of the polynomial zn − 1 into irreducible factors.
- z1−1 = z−1
- z2−1 = (z−1)·(z+1)
- z3−1 = (z−1)·(z2+z+1)
- z4−1 = (z−1)·(z+1)·(z2+1)
- z5−1 = (z−1)·(z4+z3+z2+z+1)
- z6−1 = (z−1)·(z+1)·(z2+z+1)·(z2−z+1)
- z7−1 = (z−1)·(z6+z5+z4+z3+z2+z+1)
Applying Möbius inversion to the formula gives
where μ is the Möbius function.
So the first few cyclotomic polynomials are
- Φ1(z) = z−1
- Φ2(z) = (z2−1)·(z−1)−1 = z+1
- Φ3(z) = (z3−1)·(z−1)−1 = z2+z+1
- Φ4(z) = (z4−1)·(z2−1)−1 = z2+1
- Φ5(z) = (z5−1)·(z−1)−1 = z4+z3+z2+z+1
- Φ6(z) = (z6−1)·(z3−1)−1·(z2−1)−1·(z−1) = z2−z+1
- Φ7(z) = (z7−1)·(z−1)−1 = z6+z5+z4+z3+z2+z+1
If p is a prime number, then all the pth roots of unity except 1 are primitive pth roots, and we have
Substituting any positive integer for z, this sum becomes a base z repunit. Thus a necessary (but not sufficient) condition for a repunit to be prime is that its length be prime.
Note that, contrary to first appearances, not all coefficients of all cyclotomic polynomials are 0, 1, or −1. The first exception is 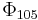 . It is not a surprise it takes this long to get an example, because the behavior of the coefficients depends not so much on n as on how many odd prime factors appear in n. More precisely, it can be shown that if n has 1 or 2 odd prime factors (e.g., n = 150) then the nth cyclotomic polynomial only has coefficients 0, 1 or −1. Thus the first conceivable n for which there could be a coefficient besides 0, 1, or −1 is a product of the three smallest odd primes, and that is 3·5·7 = 105. This by itself doesn't prove the 105th polynomial has another coefficient, but does show it is the first one which even has a chance of working (and then a computation of the coefficients shows it does). A theorem of Schur says if n has t odd prime factors then the number t-1, up to sign, occurs as a coefficient in the nth cyclotomic polynomial.
. It is not a surprise it takes this long to get an example, because the behavior of the coefficients depends not so much on n as on how many odd prime factors appear in n. More precisely, it can be shown that if n has 1 or 2 odd prime factors (e.g., n = 150) then the nth cyclotomic polynomial only has coefficients 0, 1 or −1. Thus the first conceivable n for which there could be a coefficient besides 0, 1, or −1 is a product of the three smallest odd primes, and that is 3·5·7 = 105. This by itself doesn't prove the 105th polynomial has another coefficient, but does show it is the first one which even has a chance of working (and then a computation of the coefficients shows it does). A theorem of Schur says if n has t odd prime factors then the number t-1, up to sign, occurs as a coefficient in the nth cyclotomic polynomial.
Many restrictions are known about the values that cyclotomic polynomials can assume at integer values. For example, if p is prime and d | Φp(d), then either d ≡ 1 mod (p), or d ≡ 0 mod (p).
Cyclotomic polynomials are trivially solvable in radicals, as roots of unity are themselves radicals. Moreover, there exist more informative radical expressions for nth roots of unity with the additional property[1] that every value of the expression obtained by choosing values of the radicals (for example, signs of square roots) is a primitive nth root of unity. This was already shown by Gauss in 1797[2]. Efficient algorithms exist for calculating such expressions[3].
Cyclic groups
The nth roots of unity form under multiplication a cyclic group of order n, and in fact these groups comprise all of the finite subgroups of the multiplicative group of the complex number field. A generator for this cyclic group is a primitive nth root of unity.
The nth roots of unity form an irreducible representation of any cyclic group of order n. The orthogonality relationship also follows from group-theoretic principles as described in character group.
The roots of unity appear as the eigenvectors of any circulant matrix, i.e. matrices that are invariant under cyclic shifts, a fact that also follows from group representation theory as a variant of Bloch's theorem.[4] In particular, if a circulant Hermitian matrix is considered (for example, a discretized one-dimensional Laplacian with periodic boundaries[5]), the orthogonality property immediately follows from the usual orthogonality of eigenvectors of Hermitian matrices.
Cyclotomic fields
By adjoining a primitive nth root of unity to Q, one obtains the nth cyclotomic field Fn. This field contains all nth roots of unity and is the splitting field of the nth cyclotomic polynomial over Q. The field extension Fn/Q has degree φ(n) and its Galois group is naturally isomorphic to the multiplicative group of units of the ring Z/nZ.
As the Galois group of Fn/Q is abelian, this is an abelian extension. Every subfield of a cyclotomic field is an abelian extension of the rationals. In these cases Galois theory can be written out explicitly in terms of Gaussian periods: this theory from the Disquisitiones Arithmeticae of Gauss was published many years before Galois.[6]
Conversely, every abelian extension of the rationals is such a subfield of a cyclotomic field — this is the content of a theorem of Kronecker, usually called the Kronecker-Weber theorem on the grounds that Weber completed the proof.
See also
- Circle group
- Primitive root modulo n
- Dirichlet character
- Ramanujan's sum
Notes
- ↑ Landau, Susan; Miller, Gary L. (1985), "Solvability by radicals is in polynomial time", Journal of Computer and System Sciences 30 (2): 179–208, doi:
- ↑ Gauss, Carl F. (1965). Disquisitiones Arithmeticae. Yale University Press. pp. §§359–360. ISBN 0-300-09473-6.
- ↑ Weber, Andreas; Keckeisen, Michael, Solving Cyclotomic Polynomials by Radical Expressions, http://cg.cs.uni-bonn.de/personal-pages/weber/publications/pdf/WeberA/WeberKeckeisen99a.pdf, retrieved on 2007-06-22
- ↑ T. Inui, Y. Tanabe, and Y. Onodera, Group Theory and Its Applications in Physics (Springer, 1996).
- ↑ Gilbert Strang, "The discrete cosine transform," SIAM Review 41 (1), 135-147 (1999).
- ↑ The Disquisitiones was published in 1801, Galois died in 1832 but wasn't published until 1846.
References
- Lang, Serge (2002). Algebra (revised 3rd edition ed.). New York: Springer-Verlag. ISBN 0-387-95385-X.
- Milne, James S. (1998). "Algebraic Number Theory". Course Notes.
- Milne, James S. (1997). "Class Field Theory". Course Notes.
- Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften, 322, Berlin: Springer-Verlag, MR1697859, ISBN 978-3-540-65399-8
- Neukirch, Jürgen (1986). Class Field Theory. Berlin: Springer-Verlag. ISBN 3-540-15251-2.
- Washington, Lawrence C. (1997). Cyclotomic fields (2nd edition ed.). New York: Springer-Verlag. ISBN 0-387-94762-0.
- Derbyshire, John (2006). "Roots of Unity". Unknown Quantity. Washington, D.C.: Joseph Henry Press. ISBN 0-309-09657-X. http://www.JohnDerbyshire.com/Books/Unknown/page.html.