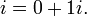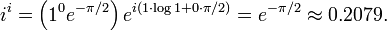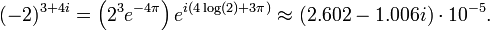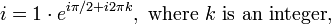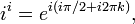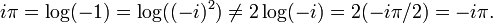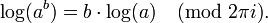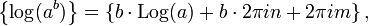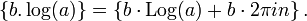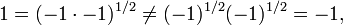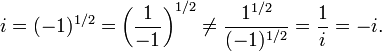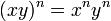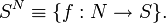Exponentiation
Exponentiation is a mathematical operation, written an, involving two numbers, the base a and the exponent n. When n is a positive integer, exponentiation corresponds to repeated multiplication:
just as multiplication by a positive integer corresponds to repeated addition:
The exponent is usually shown as a superscript to the right of the base. The exponentiation an can be read as: a raised to the n-th power, a raised to the power [of] n or possibly a raised to the exponent [of] n, or more briefly: a to the n-th power or a to the power [of] n, or even more briefly: a to the n. Some exponents have their own pronunciation: for example, a2 is usually read as a squared and a3 as a cubed.
The power an can be defined also when n is a negative integer, at least for nonzero a. No natural extension to all real a and n exists, but when the base a is a positive real number, an can be defined for all real and even complex exponents n via the exponential function ez. Trigonometric functions can be expressed in terms of complex exponentiation.
Exponentiation where the exponent is a matrix is used for solving systems of linear differential equations.
Exponentiation is used pervasively in many other fields as well, including economics, biology, chemistry, physics, and computer science, with applications such as compound interest, population growth, chemical reaction kinetics, wave behavior, and public key cryptography.

Exponentiation with integer exponents
The exponentiation operation with integer exponents requires only elementary algebra.
Positive integer exponents
The expression a2 = a·a is called the square of a because the area of a square with side-length a is a2.
The expression a3 = a·a·a is called the cube, because the volume of a cube with side-length a is a3.
So 32 is pronounced "three squared", and 23 is "two cubed".
The exponent says how many copies of the base are multiplied together. For example, 35 = 3·3·3·3·3 = 243. The base 3 appears 5 times in the repeated multiplication, because the exponent is 5. Here, 3 is the base, 5 is the exponent, and 243 is the power or, more specifically, the fifth power of 3, 3 raised to the fifth power, or 3 to the power of 5.
The word "raised" is usually omitted, and very often "power" as well, so 35 is typically pronounced "three to the fifth" or "three to the five".
Formally, powers with positive integer exponents may be defined by the initial condition a1 = a and the recurrence relation an+1 = a·an.
Exponents one and zero
Notice that 31 is the product of only one 3, which is evidently 3.
Also note that 35 = 3·34. Also 34 = 3·33. Continuing this trend, we should have
- 31 = 3·30.
Another way of saying this is that when n, m, and n − m are positive (and if x is not equal to zero), one can see by counting the number of occurrences of x that
Extended to the case that n and m are equal, the equation would read
since both the numerator and the denominator are equal. Therefore we take this as the definition of x0.
Therefore we define 30 = 1 so that the above equality holds. This leads to the following rule:
- Any number to the power 1 is itself.
- Any nonzero number to the power 0 is 1; one interpretation of these powers is as empty products. The case of 00 is discussed below.
Combinatorial interpretation
For nonnegative integers n and m, the power nm equals the cardinality of the set of m-tuples from an n-element set, or the number of m-letter words from an n-letter alphabet.
- 05 = | {} | = 0. There is no 5-tuple from the empty set.
- 14 = | { (1,1,1,1) } | = 1. There is one 4-tuple from a one-element set.
- 23 = | { (1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2), (2,2,1), (2,2,2) } | = 8. There are eight 3-tuples from a two-element set.
- 32 = | { (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3) } | = 9. There are nine 2-tuples from a three-element set.
- 41 = | { (1), (2), (3), (4) } | = 4. There are four 1-tuples from a four-element set.
- 50 = | { () } | = 1. There is exactly one empty tuple.
See also exponentiation over sets.
Negative integer exponents
By definition, raising a nonzero number to the −1 power produces its reciprocal:
One also defines
for any nonzero a and any positive integer n. Raising 0 to a negative power would imply division by 0, so it is left undefined.
The definition of a−n for nonzero a is made so that the identity aman = am+n, initially true only for nonnegative integers m and n, holds for arbitrary integers m and n. In particular, requiring this identity for m = −n is requiring
where a0 is defined above, and this motivates the definition a−n = 1/an shown above.
Exponentiation to a negative integer power can alternatively be seen as repeated division of 1 by the base. For instance,
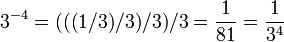 .
.
Identities and properties
The most important identity satisfied by integer exponentiation is
This identity has the consequence
for a ≠ 0, and
Another basic identity is
While addition and multiplication are commutative (for example, 2+3 = 5 = 3+2 and 2·3 = 6 = 3·2), exponentiation is not commutative: 23 = 8, but 32 = 9.
Similarly, while addition and multiplication are associative (for example, (2+3)+4 = 9 = 2+(3+4) and (2·3)·4 = 24 = 2·(3·4), exponentiation is not associative either: 23 to the 4th power is 84 or 4096, but 2 to the 34 power is 281 or 2,417,851,639,229,258,349,412,352. Without parentheses to modify the order of calculation, the order is usually understood to be top-down, not bottom-up:
Powers of ten
- See Scientific notation
In the base ten (decimal) number system, integer powers of 10 are written as the digit 1 followed or preceded by a number of zeroes determined by the sign and magnitude of the exponent. For example, 103 = 1000 and 10−4 = 0.0001.
Exponentiation with base 10 is used in scientific notation to describe large or small numbers. For instance, 299,792,458 (the speed of light in a vacuum, in meters per second) can be written as 2.99792458·108 and then approximated as 2.998·108.
SI prefixes based on powers of 10 are also used to describe small or large quantities. For example, the prefix kilo means 103 = 1000, so a kilometre is 1000 metres.
Powers of two
The positive powers of 2 are important in computer science because there are 2n possible values for an n-bit variable. See Binary numeral system.
Powers of 2 are important in set theory since a set with n members has a power set, or set of all subsets of the original set, with 2n members.
The negative powers of 2 are commonly used, and the first two have special names: half, and quarter.
In the base 2 (binary) number system, integer powers of 2 are written as 1 followed or preceded by a number of zeroes determined by the sign and magnitude of the exponent. For example, two to the power of three is written 1000 in binary.
Powers of one
The integer powers of one are one: 1n = 1.
Powers of zero
If the exponent is positive, the power of zero is zero: 0n = 0, where n > 0.
If the exponent is negative, the power of zero (0n, where n < 0) is undefined, because division by zero is implied.
If the exponent is zero, some authors define 00=1, whereas others leave it undefined, as discussed below.
Powers of minus one
If n is an even integer, then (−1)n = 1.
If n is an odd integer, then (−1)n = −1.
Because of this, powers of −1 are useful for expressing alternating sequences. For a similar discussion of powers of the complex number i, see the section on powers of the imaginary unit.
Large exponents
The limit of a sequence of powers of a number greater than one diverges, in other words they grow without bound:
- an → ∞ as n → ∞ when a > 1 .
This can be read as "a to the power of n tends to infinity as n tends to infinity when a is greater than one".
Powers of a number with absolute value less that one tend to zero:
- an → 0 as n → ∞ when |a| < 1 .
Powers of one, are one:
- an → 1 as n → ∞ when a = 1 .
If the number a varies tending to 1 as the exponent tends to infinity then the limit is not necessarily one of those above. A particularly important case is
- (1+n−1)n → e as n→∞
see the section below Powers of e.
Other limits, in particular of those tending to indeterminate forms, are described in limits of powers below.
Real powers of positive real numbers
Raising a positive real number to a power that is not an integer can be accomplished in two ways.
- Rational number exponents can be defined in terms of nth roots, and arbitrary nonzero exponents can then be defined by continuity.
- The natural logarithm can be used to define real exponents using the exponential function.
The identities and properties shown above are true for noninteger exponents as well.
Principal n-th root

An n-th root of a number a is a number x such that xn = a.
If a is a positive real number and n is a positive integer, then there is exactly one positive real solution to xn = a. This solution is called the principal n-th root of a. It is denoted n√a, where √ is the radical symbol; alternatively, it may be written  . For example: 41/2 = 2, 81/3 = 2,
. For example: 41/2 = 2, 81/3 = 2,
When one speaks of the n-th root of a positive real number a, one means the principal n-th root.
Rational powers
A power with a rational exponent m/n in lowest terms satisfies
whenever this makes sense.
Powers of e
The important mathematical constant e, sometimes called Euler's number, is approximately equal to 2.718 and is the base of the natural logarithm. It provides a path for defining exponentiation with noninteger exponents. It is defined as the following limit where the power goes to infinity as the base tends to one:
The exponential function, defined by
has the x written as a power as it satisfies the basic exponential identity
The exponential function is defined for all integer, fractional, real, and complex values of x. It can even be used to extend exponentiation to some nonnumerical entities e.g. square matrices, however the exponential identity only holds when x and y commute.
A short proof that e to a positive integer power k is the same as ek is:
This proof shows also that ex+y satisfies the exponential identity when x and y are positive integers. These results are in fact generally true for all numbers, not just for the positive integers.
Real powers
Since any real number can be approximated by rational numbers, exponentiation to an arbitrary real exponent x can be defined by continuity with the rule
where the limit as r gets close to x is taken only over rational values of r.
For example, if
then
Exponentiation by a real power is normally accomplished using logarithms instead of using limits of rational powers.
The natural logarithm ln(x) is the inverse of the exponential function ex. It is defined for 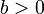 , and satisfies
, and satisfies
If bx is to be defined to as to preserve the logarithm and exponent rules, then one must have
This motivates the definition
for each real number x.
This definition of the real number power bx agrees with the definition given above using rational exponents and continuity. The definition of exponentiation using logarithms is more common in the context of complex numbers, as discussed below.
Powers of negative real numbers
If a is negative and n is even, then xn = a has no real solutions, If a is negative and n is odd, then xn = a has one negative solution.
Neither the logarithm method nor the rational exponent method can be used to define ak as a real number for a negative real number a and an arbitrary real number k. In some special cases, a definition is possible: integral powers of negative real numbers are real numbers, and rational powers of the form am/n where n is odd can be computed using roots. But since there is no real number x such that x2 = −1, the definition of am/n when n is even and m is odd must use the imaginary unit i, as described more fully in the next section.
The logarithm method cannot be used to define ak as a real number when a ≤ 0: indeed, ex is positive for every real number x, so ln(a) is not defined as a real number. (On the other hand, arbitrary complex powers of negative numbers a can be defined by choosing a complex logarithm of a.)
The rational exponent method cannot be used for negative values of a because it relies on continuity. The function f(r) = ar has a unique continuous extension from the rational numbers to the real numbers for each a > 0. But when a < 0, the function f is not even continuous on the set of rational numbers r for which it is defined.
For example, take a = −1. The nth root of −1 is −1 for every odd natural number n. So if n is an odd positive integer, (−1)(m/n) = −1 if m is odd, and (−1)(m/n) = 1 if m is even. Thus the set of rational numbers q for which −1q = 1 is dense in the rational numbers, as is the set of q for which −1q = −1. This means that the function (−1)q is not continuous at any rational number q where it is defined.
Complex powers of positive real numbers
Imaginary powers of e

The geometric interpretation of the operations on complex numbers and the definition of powers of e is the clue to understanding eix for real x. Consider the right triangle (0, 1, 1 + ix/n). For big values of n the triangle is almost a circular sector with a small central angle equal to x/n radians. The triangles (0, (1 + ix/n)k, (1 + ix/n)k+1) are mutually similar for all values of k. So for large values of n the limiting point of (1 + ix/n)n is the point on the unit circle whose angle from the positive real axis is x radians. The polar coordinates of this point are (r, θ) = (1, x), and the cartesian coordinates are (cos x, sin x). So e ix = cos x + isin x, and this is Euler's formula, connecting algebra to trigonometry by means of complex numbers.
The solutions to the equation ez = 1 are the integer multiples of 2iπ:
More generally, if eb = a, then every solution to ez = a can be obtained by adding an integer multiple of 2πi to b:
Thus the complex exponential function is a periodic function with period 2πi.
More simply: eiπ = −1; ex + iy = ex(cos y + i sin y).
Trigonometric functions
It follows from Euler's formula that the trigonometric functions cosine and sine are
Historically, cosine and sine were defined geometrically before the invention of complex numbers. The above formula reduces the complicated formulas for trigonometric functions of a sum into the simple exponentiation formula
Using exponentiation with complex exponents many problems in trigonometry can be reduced to algebra.
Complex powers of e
The power ex+i·y is computed ex · ei·y. The real factor ex is the absolute value of ex+i·y and the complex factor ei·y identifies the direction of ex+i·y.
Complex powers of positive real numbers
If a is a positive real number, and z is any complex number, the power az is defined as ez·ln(a), where x = ln(a) is the unique real solution to the equation ex = a. So the same method working for real exponents also works for complex exponents. For example:
- 2 i = e i·ln(2) = cos(ln(2))+i·sin(ln(2)) = 0.7692+i·0.63896
- e i = 0.54030+i·0.84147
- 10 i = −0.66820+i·0.74398
- (e 2·π) i = 535.49 i = 1
Powers of complex numbers
Integer powers of complex numbers are defined by repeated multiplication or division as above. Complex powers of positive reals are defined via ex as above. These are continuous functions. Trying to extend these functions to the general case of noninteger powers of complex numbers that are not positive reals leads to difficulties. Either we define discontinuous functions or multivalued functions. Neither of these options is entirely satisfactory.
The rational power of a complex number must be the solution to an algebraic equation. Therefore it always has a finite number of possible values. For example, w = z1/2 must be a solution to the equation w2 = z. But if w is a solution, then so is −w, because (−1)2 = 1 . A unique but somewhat arbitary solution called the principal value can be chosen using a general rule which also applies for nonrational powers.
Complex powers and logarithms are more naturally handled as single valued functions on a Riemann surface. Single valued versions are defined by choosing a sheet. The value has a discontinuity along a branch cut. Choosing one out of many solutions as the principal value leaves us with functions that are not continuous, and the usual rules for manipulating powers can lead us astray.
Any nonrational power of a complex number has an infinite number of possible values because of the multi-valued nature of the complex logarithm (see below). The principal value is a single value chosen from these by a rule which, amongst its other properties, ensures powers of complex numbers with a positive real part and zero imaginary part give the same value as for the corresponding real numbers.
Exponentiating a real number to a complex power is formally a different operation from that for the corresponding complex number. However in the common case of a positive real number the principal value is the same. The powers of negative real numbers are not always defined and are discontinuous even where defined. When dealing with complex numbers the complex number operation is normally used instead. For example: (−1)1/3 = −1 as a real, but when dealing with complex numbers (−1)1/3 normally means either the principal value eπi/3 or the set of values {eπi/3, e−πi/3, −1}.
Powers of the imaginary unit
If i is the imaginary unit and n is an integer, then in equals 1, i, −1, or −i, according to whether the integer n is congruent to 0, 1, 2, or 3 modulo 4. Because of this, the powers of i are useful for expressing sequences of period 4.
Complex power of a complex number
For complex numbers a and b with a ≠ 0, the notation ab is ambiguous in the same sense that log a is.
To obtain a value of ab, first choose a logarithm of a; call it log a. Such a choice may be the principal value Log a (the default, if no other specification is given), or perhaps a value given by some other branch of log z fixed in advance. Then, using the complex exponential function one defines
because this agrees with the earlier definition in the case where a is a positive real number and the (real) principal value of log a is used.
If b is an integer, then the value of ab is independent of the choice of log a, and it agrees with the earlier definition of exponentation with an integer exponent.
If b is a rational number n/m in lowest terms with m > 0, then the infinitely many choices of log a yield only m different values for ab; these values are the m complex solutions z to the equation zm = an.
If b is an irrational number, then the infinitely many choices of log a lead to infinitely many distinct values for ab.
The computation of complex powers is facilitated by converting the base a to polar form, as described in detail below.
Complex roots of unity
A complex number a such that an = 1 for a positive integer n is an nth root of unity. Geometrically, the nth roots of unity lie on the unit circle of the complex plane at the vertices of a regular n-gon with one vertex on the real number 1.
If zn = 1 but zk ≠ 1 for all natural numbers k such that 0 < k < n, then z is called a primitive nth root of unity. The negative unit −1 is the only primitive square root of unity. The imaginary unit i is one of the two primitive 4-th roots of unity; the other one is −i.
The number e2πi (1/n) is the primitive nth root of unity with the smallest positive complex argument. (It is sometimes called the principal nth root of unity, although this terminology is not universal and should not be confused with the principal value of n√1, which is 1.[1])
The other nth roots of unity are given by
for 2 ≤ k ≤ n.
Roots of arbitrary complex numbers
Although there are infinitely many possible values for a general complex logarithm, there are only a finite number of values for the power az in the important special case where z = 1/n and n is a positive integer. These are the nth roots of a; they are solutions of the equation xn = a. As with real roots, a second root is also called a square root and a third root is also called a cube root.
It is conventional in mathematics to define a1/n as the principal value of the root. If a is a positive real number, it is also conventional to select a positive real number as the principal value of the root a1/n. For general complex numbers, the nth root with the smallest argument is often selected as the principal value of the nth root operation, as with principal values of roots of unity.
The set of nth roots of a complex number a is obtained by multiplying the principal value a1/n by each of the nth roots of unity. For example, the fourth roots of 16 are 2, −2, 2i, and −2i, because the principal value of the fourth root of 16 is 2 and the fourth roots of unity are 1, −1, i, and −i.
Computing complex powers
It is often easier to compute complex powers by writing the number to be exponentiated in polar form. Every complex number z can be written in the polar form
where r is a nonnegative real number and θ is the (real) argument of z. The polar form has a simple geometric interpretation: if a complex number u + iv is thought of as representing a point (u, v) in the complex plane using Cartesian coordinates, then (r, θ) is the same point in polar coordinates. That is, r is the "radius" r2 = u2 + v2 and θ is the "angle" θ = atan2(v, u). The polar angle θ is ambiguous since any multiple of 2π could be added to θ without changing the location of the point. Each choice of θ gives in general a different possible value of the power. A branch cut can be used to choose a specific value. The principal value (the most common branch cut), corresponds to θ chosen in the interval (−π, π]. For complex numbers with a positive real part and zero imaginary part using the principal value gives the same result as using the corresponding real number.
In order to compute the complex power ab, write a in polar form:
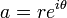 .
.
Then
and thus
If b is decomposed as c + di, then the formula for ab can be written more explicitly as
This final formula allows complex powers to be computed easily from decompositions of the base into polar form and the exponent into Cartesian form. It is shown here both in polar form and in Cartesian form (via Euler's identity).
The following examples use the principal value, the branch cut which causes θ to be in the interval (−π, π]. To compute ii, write i in polar and Cartesian forms:
Then the formula above, with r = 1, θ = π/2, c = 0, and d = 1, yields:
Similarly, to find (−2)3 + 4i, compute the polar form of −2,
and use the formula above to compute
The value of a complex power depends on the branch used. For example, if the polar form i = 1ei(5π/2) is used to compute i i, the power is found to be e−5π/2; the principal value of i i, computed above, is e−π/2. The set of all possible values for i i is given by:[2]
So there is an infinity of values which are possible candidates for the value of ii, one for each integer k. All of them have a zero imaginary part so one can say ii has an infinity of valid real values.
Failure of power and logarithm identities
Some identities for powers and logarithms for positive real numbers will fail for complex numbers, no matter how complex powers and complex logarithms are defined.
For example,
- The identity log(ab) = b · log a holds whenever a is a positive real number and b is a real number. But for the principal branch of the complex logarithm one has
-
- Regardless of which branch of the logarithm is used, a similar failure of the identity will exist. The best that can be said is that:
- This identity does not hold even when considering log as a multivalued function. The possible values of log(ab) contain those of b · log a as a subset. Using Log(a) for the principal value of log(a) and m, n as any integers the possible values of both sides are:
- The identities (ab)c = acbc and (a/b)c = ac/bc are valid when a and b are positive real numbers and c is a real number. But a calculation using principal branches shows that
-
- and
- On the other hand, when c is an integer, the identities are valid for all nonzero complex numbers.
- If exponentiation is considered as a multivalued function then the possible values of (−1.−1)1/2 are {1, −1}. The identity holds but saying {1} = {(−1.−1)1/2} is wrong.
- The identity (ea)b = eab holds for real numbers a and b, but assuming its truth for complex numbers leads to the following paradox, discovered in 1827 by Clausen:[3] For any integer n,
-
- e1+2πin = e1e2πin = e·1 = e,
- (e1+2πin)1+2πin = e,
- e1+4πin−4π2n2 = e,
- e1e4πine−4π2n2 = e, and
- e−4π2n2 = 1,
- but this is false when the integer n is nonzero.
- There are a number of problems in the reasoning:
- The major error is that changing the order of exponentiation in going from line two to three changes what the principal value chosen will be.
- From the multi valued point of view the first error occurs even sooner, it is implicit in the first line and not obvious. It is that e is a real number whereas the result of e1+2πin is a complex number better represented as e+0i. Substituting the complex number for the real on the second line makes the power have multiple possible values. Changing the order of exponentiation from lines two to three also affects how many possible values the result can have.
Zero to the zero power

Most authors agree with the statements related to 00 in the two lists below, but come to differing conclusions when it comes to defining 00 or not: see the next subsection.
In most settings not involving continuity (for instance, those in which only integral exponents are considered), interpreting 00 as 1 simplifies formulas and eliminates the need for special cases in theorems. (See the next paragraph for some settings that do involve continuity.) For example:
- Regarding 00 as an empty product of zeros suggests a value of 1.
- The combinatorial interpretation of 00 is the number of empty tuples of elements from the empty set. There is exactly one empty tuple.
- Equivalently, the set-theoretic interpretation of 00 is the number of functions from the empty set to the empty set. There is exactly one such function, the empty function.[4]
- It greatly simplifies the theory of polynomials and power series that a constant term can be written ax0 for an arbitrary x. For example:
- The formula for the coefficients of a product of polynomials would lose much of its simplicity if constant terms had to be treated specially.
- Identities like
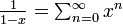 and
and 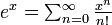 are not valid for x = 0 unless 00 = 1.
are not valid for x = 0 unless 00 = 1. - The binomial theorem
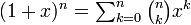 is not valid for x = 0 unless 00 = 1.[5]
is not valid for x = 0 unless 00 = 1.[5]
- In differential calculus, the power rule
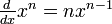 is not valid for n = 1 at x = 0 unless 00 = 1.
is not valid for n = 1 at x = 0 unless 00 = 1.
On the other hand, 00 must be handled as an indeterminate form in settings where the exponent varies continuously:
- When f(t) and g(t) are real-valued functions approaching 0 (as t approaches a real number or ±∞), with f(t) > 0, the function f(t)g(t) need not approach 1. In fact, depending on f and g, the limit of f(t)g(t) can be any nonnegative real number or +∞, or it can be undefined. Limits involving algebraic operations can often be evaluated by replacing subexpressions by their limits; if the resulting expression does not determine the original limit, the expression is known as an indeterminate form.[6]
- For example, the following expressions are all of the form f(t)g(t) with f(t),g(t) → 0 as t → 0+, and have the stated limits for any positive constant a:

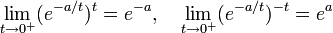 .
.
- The limits are all different so clearly no single value of 00 can be defined as the limit for every case. This behavior results from the fact that the two-variable function xy, though continuous on the set {(x,y): x > 0}, cannot be extended to a continuous function on any set containing (0,0), no matter how 00 is defined.[7]
- The function zz is defined for nonzero complex numbers z by choosing a branch of log z and setting zz := ez log z, but there is no branch of log z defined at z = 0, let alone in a neighborhood of 0.[8] There is no holomorphic function defined in a neighborhood of 0 that agrees with zz for all positive real numbers z.
History of differing points of view
Different authors interpret the situation above in different ways:
- Some argue that the best value for 00 depends on context, and hence that defining it once and for all is problematic.[9] According to Benson (1999), "The choice whether to define 00 is based on convenience, not on correctness."[10]
- Others argue that 00 is 1. According to p. 408 of Knuth (1992), it "has to be 1".[11]
The debate has been going on at least since the early 1800s. At that time, most mathematicians agreed that 00 = 1, but in 1821 Cauchy[12] listed 00 along with expressions like 0/0 in a table of undefined forms. In the 1830s Libri[13][14] published an unconvincing argument for 00 = 1, and Möbius[15] sided with him, erroneously claiming that 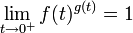 whenever
whenever 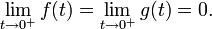 A commentator who signed his name simply as "S" provided the counterexample of (e−1/t)t (which can be obtained in one example above by taking a = 1), and this quieted the debate for some time, with the apparent conclusion of this episode being that 00 should be undefined. More details can be found in Knuth (1992).[11]
A commentator who signed his name simply as "S" provided the counterexample of (e−1/t)t (which can be obtained in one example above by taking a = 1), and this quieted the debate for some time, with the apparent conclusion of this episode being that 00 should be undefined. More details can be found in Knuth (1992).[11]
Treatment in programming languages and calculators
Computer programming languages that evaluate 00 to 1[16] include bc, Haskell, J, Java, MATLAB, ML, Perl, Python, R, Ruby, Scheme, and SQL. In the .NET Framework, the method System.Math.Pow treats 00 to be 1.
Microsoft Excel issues an error when it evaluates 00.
Microsoft Windows' Calculator and the calculator in Google search[17] evaluate 00 to 1.
Maple simplifies a0 to 1 and 0a to 0, even if no constraints are placed on a, and evaluates 00 to 1.
Mathematica simplifies a0 to 1, even if no constraints are placed on a. It does not simplify 0a, and it takes 00 to be an indeterminate form.
Limits of powers
The section zero to the zero power shows a number of examples of limits which tend to the indeterminate form 00. Each of the examples tends to a different value. More generally, viewing the set D = {(x,y): x > 0} as a subset of R2 (that is, the set of all pairs (x,y) with x,y belonging to the extended real number line R = [−∞, +∞], endowed with the product topology), the function xy defined on D has a limit at all accumulation points of D, except for (0,0), (+∞,0), (1,+∞) and (1,−∞).[18] Accordingly, this allows one to define the powers xy by continuity whenever 0 ≤ x ≤ +∞, −∞ ≤ y ≤ +∞, except for 00, (+∞)0, 1+∞ and 1−∞, which remain indeterminate forms. This method does not permit a definition of xy when x < 0, since pairs (x,y) with x < 0 are not accumulation points of D.
The section large powers describes the indeterminate form 1+∞ plus the cases of the limit of an → ∞ as n → ∞ when a > 1 and when 0 < a < 1.
Efficiently computing a power
The simplest method of computing an requires n−1 multiplication operations, but it can be computed more efficiently as illustrated by the following example. To compute 2100, note that 100 = 96 + 4 and 96 = 3*32. Compute the following in order:
- 22 = 4
- (22)2 = 24 = 16
- (24)2 = 28 = 256
- (28)2 = 216 = 65,536
- (216)2 = 232 = 4,294,967,296
- 232 232 23224 = 2100
This series of steps only requires 8 multiplication operations instead of 99.
In general, the number of multiplication operations required to compute an can be reduced to Θ(log n) by using exponentiation by squaring or (more generally) addition-chain exponentiation. Finding the minimal sequence of multiplications (the minimal-length addition chain for the exponent) for an is a difficult problem for which no efficient algorithms are currently known, but many reasonably efficient heuristic algorithms are available.
Exponential notation for function names
Placing an integer superscript after the name or symbol of a function, as if the function were being raised to a power, commonly refers to repeated function composition rather than repeated multiplication. Thus f3(x) may mean f(f(f(x))); in particular, f −1(x) usually denotes the inverse function of f. Iterated functions are of interest in the study of fractals and dynamical systems. Babbage was the first to study the problem of finding a functional square root f1/2(x).
However, for historical reasons, a special syntax applies to the trigonometric functions: a positive exponent applied to the function's abbreviation means that the result is raised to that power, while an exponent of −1 denotes the inverse function. That is, sin2x is just a shorthand way to write (sin x)2 without using parentheses, whereas sin−1x refers to the inverse function of the sine, also called arcsin x. There is no need for a shorthand for the reciprocals of trigonometric functions since each has its own name and abbreviation; for example, 1/sin x = (sin x)−1 is csc x. A similar convention applies to logarithms, where log2x usually means (log x)2, not log log x.
Generalizations of exponentiation
Exponentiation in abstract algebra
Exponentiation for integer exponents can be defined for quite general structures in abstract algebra.
Let X be a set with a power-associative binary operation which is written multiplicatively,. Then xn is defined for any element x of X and any nonzero natural number n as x multiplied by itself n times.
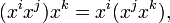 Power associative
Power associative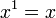
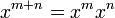
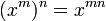
If the operation has a two-sided identity element 1 (often denoted by e), then x0 is defined to be equal to 1 for any x.
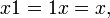 Two sided identity
Two sided identity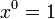
If the operation also has two-sided inverses, and multiplication is associative then the magma is a group. The inverse of x can be denoted by x−1 and follows all the usual rules for exponents.
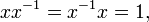 Two sided inverse
Two sided inverse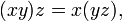 Associative
Associative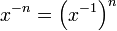

If the multiplication operation is commutative (as for instance in abelian groups), then the following holds:
If the binary operation is written additively, as it often is for abelian groups, then "exponentiation is repeated multiplication" can be reinterpreted as "multiplication is repeated addition". Thus, each of the laws of exponentiation above has an analogue among laws of multiplication.
When one has several operations around, any of which might be repeated using exponentiation, it is common to indicate which operation is being repeated by placing its symbol in the superscript. Thus, x*n is x * ··· * x, while x#n is x # ··· # x, whatever the operations * and # might be.
Superscript notation is also used, especially in group theory, to indicate conjugation. That is, gh = h−1gh, where g and h are elements of some group. Although conjugation obeys some of the same laws as exponentiation, it is not an example of repeated multiplication in any sense. A quandle is an algebraic structure in which these laws of conjugation play a central role.
Exponentiation over sets
If n is a natural number and A is an arbitrary set, the expression An is often used to denote the set of ordered n-tuples of elements of A. This is equivalent to letting An denote the set of functions from the set {0, 1, 2, ..., n−1} to the set A; the n-tuple (a0, a1, a2, ..., an−1) represents the function that sends i to ai.
For an infinite cardinal number κ and a set A, the notation Aκ is also used to denote the set of all functions from a set of size κ to A. This is sometimes written κA to distinguish it from cardinal exponentiation, defined below.
This generalized exponential can also be defined for operations on sets or for sets with extra structure. For example, in linear algebra, it makes sense to index direct sums of vector spaces over arbitrary index sets. That is, we can speak of
where each Vi is a vector space. Then if Vi = V for each i, the resulting direct sum can be written in exponential notation as V(+)N, or simply VN with the understanding that the direct sum is the default. We can again replace the set N with a cardinal number n to get Vn, although without choosing a specific standard set with cardinality n, this is defined only up to isomorphism. Taking V to be the field R of real numbers (thought of as a vector space over itself) and n to be some natural number, we get the vector space that is most commonly studied in linear algebra, the Euclidean space Rn.
If the base of the exponentiation operation is a set, the exponentiation operation is the Cartesian product unless otherwise stated. Since multiple Cartesian products produce an n-tuple, which can be represented by a function on a set of appropriate cardinality, SN becomes simply the set of all functions from N to S in this case:
This fits in with the exponentiation of cardinal numbers, in the sense that |SN| = |S||N|, where |X| is the cardinality of X. When N=2={0,1}, we have |2X| = 2|X|, where 2X, usually denoted by PX, is the power set of X; each subset Y of X corresponds uniquely to a function on X taking the value 1 for x ∈ Y and 0 for x ∉ Y.
Exponentiation in category theory
In a Cartesian closed category, the exponential operation can be used to raise an arbitrary object to the power of another object. This generalizes the Cartesian product in the category of sets.
Exponentiation of cardinal and ordinal numbers
In set theory, there are exponential operations for cardinal and ordinal numbers.
If κ and λ are cardinal numbers, the expression κλ represents the cardinality of the set of functions from any set of cardinality λ to any set of cardinality κ.[4] If κ and λ are finite, then this agrees with the ordinary arithmetic exponential operation. For example, the set of 3-tuples of elements from a 2-element set has cardinality 8 = 23.
Exponentiation of cardinal numbers is distinct from exponentiation of ordinal numbers, which is defined by a limit process involving transfinite induction.
Repeated exponentiation
Just as exponentiation of natural numbers is motivated by repeated multiplication, it is possible to define an operation based on repeated exponentiation; this operation is sometimes called tetration. Iterating tetration leads to another operation, and so on. This sequence of operations is expressed by the Ackermann function and Knuth's up-arrow notation.
Exponentiation in programming languages
The superscript notation xy is convenient in handwriting but inconvenient for typewriters and computer terminals that align the baselines of all characters on each line. Many programming languages have alternate ways of expressing exponentiation that do not use superscripts:
- x ↑ y: Algol, Commodore BASIC
- x ^ y: BASIC, J, Matlab, R, Microsoft Excel, TeX (and its derivatives), Haskell (for integer exponents), and most computer algebra systems
- x ** y: Ada, Bash, COBOL, Fortran, FoxPro, Perl, PL/I, Python, Ruby, SAS, ABAP, Haskell (for floating-point exponents), Turing
- x * y: APL
- Power(x, y): Microsoft Excel, Delphi/Pascal (declared in "Math"-unit)
- pow(x, y): C, C++, PHP
- Math.pow(x, y): Java, JavaScript, Modula-3
- Math.Pow(x, y): C#
- (expt x y): Common Lisp, Scheme
In Bash, C, C++, C#, Java, JavaScript, Perl, PHP, Python and Ruby, the symbol ^ represents bitwise XOR. In Pascal, it represents indirection.
History of the notation
The term power was used by Euclid for the square of a line. Nicolas Chuquet used a form of exponential notation in the 15th century, which was later used by Henricus Grammateus and Michael Stifel. Samuel Jeake introduced the term indices in 1696.[19] In the 16th century Robert Recorde used the terms square, cube, zenzizenzic (fourth power), surfolide (fifth), zenzicube (sixth), second surfolide (seventh) and Zenzizenzizenzic (eighth). Biquadrate has been used to refer to the fourth power as well.
Some mathematicians (e.g., Isaac Newton) used exponents only for powers greater than two, preferring to represent squares as repeated multiplication. Thus they would write polynomials, for example, as ax + bxx + cx3 + d.
Another historical synonym, involution,[20] is now rare and should not be confused with its more common meaning.
See also
- Exponential function
- Exponential growth and exponential decay
- List of exponential topics
- Logarithm and complex logarithm
- Modular exponentiation
- Nth root
- Tetration
- Unicode subscripts and superscripts
References
- ↑ This definition of a principal root of unity can be found in:
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein (2001). Introduction to Algorithms (second edition ed.). MIT Press. ISBN 0262032937. Online resource
- Paul Cull, Mary Flahive, and Robby Robson (2005). Difference Equations: From Rabbits to Chaos (Undergraduate Texts in Mathematics ed.). Springer. ISBN 0387232346. Defined on page 351, available on Google books.
- "Principal root of unity", MathWorld.
- ↑ Complex number to a complex power may be real at Cut The Knot gives some references to ii
- ↑ Thomas Clausen, Journal für die reine und angewandte Mathematik 2 (1827), 286–287.
- ↑ 4.0 4.1 N. Bourbaki, Elements of Mathematics, Theory of Sets, Springer-Verlag, 2004, III.§3.5.
- ↑ "Some textbooks leave the quantity 00 undefined, because the functions x0 and 0x have different limiting values when x decreases to 0. But this is a mistake. We must define x0 = 1, for all x, if the binomial theorem is to be valid when x = 0, y = 0, and/or x = −y. The binomial theorem is too important to be arbitrarily restricted! By contrast, the function 0x is quite unimportant".Ronald Graham, Donald Knuth, and Oren Patashnik (1989-01-05). "Binomial coefficients". Concrete Mathematics (1st edition ed.). Addison Wesley Longman Publishing Co. pp. 162. ISBN 0-201-14236-8.
- ↑ Malik, S. C.; Savita Arora (1992). Mathematical Analysis. pp. 223. ISBN 978-8122403237. "In general the limit of φ(x)/ψ(x) when x=a in case the limits of both the functions exist is equal to the limit of the numerator divided by the denominator. But what happens when both limits are zero? The division (0/0) then becomes meaningless. A case like this is known as an indeterminate form. Other such forms are ∞/∞ 0×∞, ∞−∞, 00, 1∞ and ∞0".
- ↑ L. J. Paige (March 1954). "A note on indeterminate forms". American Mathematical Monthly 61 (3): 189–190. doi:.
- ↑ "... Let's start at x = 0. Here xx is undefined." Mark D. Meyerson, The Xx Spindle, Mathematics Magazine 69, no. 3 (June 1996), 198-206.
- ↑ Examples include Edwards and Penny (1994). Calculus, 4th ed,, Prentice-Hall, p. 466, and Keedy, Bittinger, and Smith (1982). Algebra Two. Addison-Wesley, p. 32.
- ↑ Donald C. Benson, The Moment of Proof : Mathematical Epiphanies. New York Oxford University Press (UK), 1999. ISBN 9780195117219
- ↑ 11.0 11.1 Donald E. Knuth, Two notes on notation, Amer. Math. Monthly 99 no. 5 (May 1992), 403–422.
- ↑ Augustin-Louis Cauchy, Cours d'Analyse de l'École Royale Polytechnique (1821). In his Oeuvres Complètes, series 2, volume 3.
- ↑ Guillaume Libri, Note sur les valeurs de la fonction 00x, Journal für die reine und angewandte Mathematik 6 (1830), 67–72.
- ↑ Guillaume Libri, Mémoire sur les fonctions discontinues, Journal für die reine und angewandte Mathematik 10 (1833), 303–316.
- ↑ A. F. Möbius, Beweis der Gleichung 00 = 1, nach J. F. Pfaff, Journal für die reine und angewandte Mathematik 12 (1834), 134–136.
- ↑ For example, see John Benito (April 2003). "Rationale for International Standard — Programming Languages — C" (PDF). Revision 5.10.
- ↑ http://www.google.co.uk/search?q=0%5E0
- ↑ N. Bourbaki, Topologie générale, V.4.2.
- ↑ O'Connor, John J.; Robertson, Edmund F., "Etymology of some common mathematical terms", MacTutor History of Mathematics archive
- ↑ This definition of "involution" appears in the OED second edition, 1989, and Merriam-Webster online dictionary [1]. The most recent usage in this sense cited by the OED is from 1806.
External links
- sci.math FAQ: What is 00?
- Introducing 0th power on PlanetMath
- Laws of Exponents with derivation and examples
- 1058 Powers of Two
- 10,000 powers of two (14.5 MB)
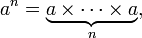
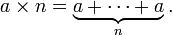
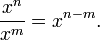

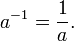

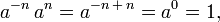
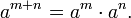
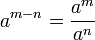
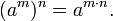
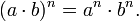
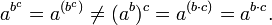
![a^{m/n} = \left(a^m\right)^{1/n} = \sqrt[n]{a^m}](/2009-wikipedia_en_wp1-0.7_2009-05/I/40f6813960fd078b8ad96dc1b8c1dbaa.png)
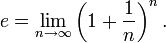
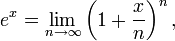
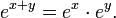
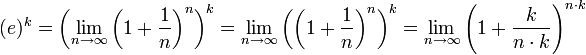
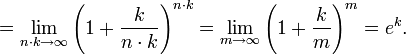
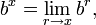
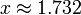
![5^x \approx 5^{1.732} =5^{433/250}=\sqrt[250]{5^{433}} \approx 16.241 .](/2009-wikipedia_en_wp1-0.7_2009-05/I/111f8b7060d6aaabeb6f7be93c74f13e.png)
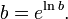
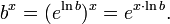
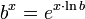
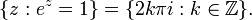


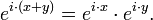
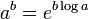
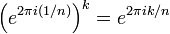
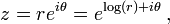
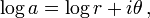
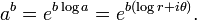
![\left( r^c e^{-d\theta} \right) e^{i (d \log r + c\theta)} = \left( r^c e^{-d\theta} \right) \left[ \cos(d \log r + c\theta) + i \sin(d \log r + c\theta) \right].](/2009-wikipedia_en_wp1-0.7_2009-05/I/80303055b1b938c4992bae52d873c3a9.png)