Polytope

In geometry, polytope is a generic term that can refer to a two-dimensional polygon, a three-dimensional polyhedron, or any of the various generalizations thereof, including generalizations to higher dimensions (such as a polychoron in four dimensions) and other abstractions (such as unbounded polytopes, apeirotopes, tessellations, and abstract polytopes).

When referring to an n-dimensional generalization, the term n-polytope is used. For example, a polygon is a 2-polytope, a polyhedron is a 3-polytope, and a polychoron is a 4-polytope.

The term was coined by Alicia Boole, the daughter of logician George Boole.

History

The concept of a polytope originally began with polygons and polyhedra, both of which have been known since ancient times. The regular polygons were known to the ancient Greeks, and the pentagram, a non-convex regular polygon (star polygon), appears on the vase of Aristophonus, Caere, dated to the 7th century B.C.. The Platonic solids, which are regular polyhedra, were a major focus of study of ancient Greek mathematicians (most notably Euclid's Elements), probably because of their intrinsic aesthetic qualities. Pythagoras knew three of them, and Theaetetus (circa 417 B. C.) described all five. Archimedes described the Archimedean solids, which are uniform polyhedra, in a now-lost work.

After the ancient Greeks, however, the subject did not see much development for a long time. Even though the pentagram was known since ancient times, non-convex polygons in general were not systematically studied until the 14th century by Thomas Bredwardine. Although non-convex polyhedra were also known early on, it was not until 1619 that Johannes Kepler first recognized that the Kepler-Poinsot polyhedra are regular, on par with the Platonic solids.

The 19th century was a time when the subject saw significant advances. In 1854, Bernhard Riemann introduced the possibility of geometry in dimensions higher than 3, thus opening up the possibility of higher-dimensional analogues of polygons and polyhedra. In 1882, Hoppe first coined the word polytope to refer to this more general concept of polygons and polyhedra. This term was first used by Alicia Boole Stott ten years later. Around the same time, in 1901, Ludwig Schläfli systematically described all the regular polytopes in n dimensions (he used the term polyschem for what we now call polytope). In 1895, Thorold Gosset rediscovered the 6 convex regular 4-polytopes, and proceeded to investigate generalizations of the semiregular polytopes to higher dimensions as well as higher-dimensional space tesselations.

More recently, in the 20th century, the concept of a polytope has been further generalized by researchers such as H. S. M. Coxeter, and the theory of abstract polytopes developed. The Uniform Polychora Project was founded by Norman Johnson, John Horton Conway, and others in an attempt to eventually classify all uniform polytopes in n dimensions, both convex and non-convex.

In modern times, polytopes and related concepts have found important applications in computer graphics, optimization, search engines and numerous other fields.

Properties

A polytope may be convex. The convex polytopes are the simplest kind of polytopes, and form the basis for different generalizations of the concept of polytopes.

A polytope may be regular. The regular polytopes are a class of highly-symmetrical and aesthetically-pleasing polytopes, including the Platonic solids, which have been studied extensively since ancient times.

A non-convex polytope may be self-intersecting; this class of polytopes include the star polytopes.

Elements

An n-dimensional polytope is bounded by a number of (n−1)-dimensional facets. These facets are themselves polytopes, whose facets are (n−2)-dimensional ridges of the original polytope. Every ridge arises as the intersection of two facets (but the intersection of two facets need not be a ridge). Ridges are once again polytopes whose facets give rise to (n−3)-dimensional boundaries of the original polytope, and so on. These bounding sub-polytopes may be referred to as faces, or specifically k-dimensional faces or k-faces. A 0-dimensional face is called a vertex, and consists of a single point. A 1-dimensional face is called an edge, and consists of a line segment. A 2-dimensional face consists of a polygon, and a 3-dimensional face, sometimes called a cell, consists of a polyhedron.

Dimension of element	Element name (in a d-polytope)
0	Vertex
1	Edge
2	Face
3	Cell
n	n-face - elements order n = 2, 3, ..., d − 1
d − 3	Peak - (d−3)-face
d − 2	Ridge or subfacet - (d−2)-face
d − 1	Facet - (d−1)-face
d	Body - d-face

Note that this terminology is not fully standardized. Existing literature uses terms that are not entirely consistent across different authors. Some authors use face to refer to a facet, while others use face to denote a 2-face specifically. Some sources use edge to refer to a ridge. H. S. M. Coxeter uses cell to denote facet.

Different approaches to defining polytopes

The term polytope is a broad term that covers a wide class of objects, and different definitions are attested in mathematical literature. Many of these definitions are not equivalent, resulting in different sets of objects being called polytopes. They represent different approaches of generalizing the convex polytopes to include other objects with similar properties and aesthetic beauty.

For example, one approach begins with the 0-dimensional vertex as a 0-polytope (vertices). A 1-dimensional 1-polytope (edge) is constructed by two 0-polytopes. Then 2-polytopes (polygons) are defined as objects whose facets (edges) are 1-polytopes, and 3-polytopes (polyhedra) are defined as objects whose facets (faces) are 2-polytopes, and so forth.

A more modern approach defines a polytope any set of points that admits a simplicial decomposition (see section below), under the observation that all convex polytopes can be decomposed into a union of simplices satisfying certain properties.

A polytope may also be regarded as a tessellation of some given manifold. Under this definition, plane tilings and space tilings are considered to be polytopes, and convex polytopes are regarded to be tilings of elliptic space. Tilings of hyperbolic space are also included under this definition.

The theory of abstract polytopes attempts to detach polytopes from the space containing them, considering their purely combinatorial properties. This allows the definition of the term to be extended to include objects for which it is difficult to define clearly a natural underlying space.

Simplicial decomposition

Given a convex r-dimensional polytope P, a subset of its vertices containing (r+1) linearly independent points defines an r-simplex. It is possible to form a collection of subsets such that the union of the corresponding simplices is equal to P, and the intersection of any two simplices is either empty or a lower-dimensional simplex.

For example, a square has four vertices (its corners). It can be decomposed into two triangles (2-simplices) by dividing it along one of its diagonals. The union of these two triangles is the original square, and their intersection is the diagonal of the square (a 1-simplex, which is the same as a line segment).

Any set of points that can be decomposed into r-simplices in this way is said to have a r-simplicial decomposition. So, the square in the above example has a 2-simplicial decomposition. All convex polytopes have simplicial decompositions; hence, one may define an r-polytope as a set that admits an r-simplicial decomposition. (This definition is attributed to Alexandrov. For a more abstract treatment, see simplicial complex.)

Note that although this definition includes the convex polytopes, it also admits a more general class of objects. For example, a line segment is a 1-polytope under this definition, and so is anything obtained by joining line segments end-to-end:

If every vertex in the 1-polytope has exactly two line segments meeting at it (all except the last example above), it is a topological curve, called a polygonal curve. One may categorize these as open or closed, depending on whether the ends are joined, and as simple or complex, depending on whether they intersect themselves. Closed polygonal curves are called polygons.

Simple polygons in the plane are Jordan curves: they have an interior that is a topological disk. So does a 2-polytope (as can be seen in the third example above), and these are often treated interchangeably with their boundary, the word polygon referring to either.

Now polygons, in turn, can be joined along edges (1-faces), giving a polyhedral surface, called a skew polygon when open and a polyhedron when closed. Simple (non-self-intersecting) polyhedra are interchangeable with their interiors, which are 3-polytopes that can be used to build 4-dimensional forms (sometimes called polychora), and the process can be repeated to obtain the higher polytopes.

Self-dual polytopes

The 5-cell (4-simplex) is self-dual with 5 vertices and 5 tetrahedral cells.

In 2 dimensions, all regular polygons (regular 2-polytopes) are self-dual.

In 3 dimensions, the tetrahedron is self-dual, as well as canonical polygonal pyramids and elongated pyramids.

In higher dimensions, every regular n-simplex, with Schlafli symbol {3ⁿ}, is self-dual.

In addition, the 24-cell in 4 dimensions, with Schlafli symbol {3,4,3}, is self-dual.

Uses

In the study of optimization, linear programming studies the maxima and minima of linear functions constricted to the boundary of an 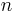-dimensional polytope.

References

• Coxeter, Harold Scott MacDonald (1973), Regular Polytopes, New York: Dover Publications, ISBN 978-0-486-61480-9 .
• Grünbaum, Branko (2003), Kaibel, Volker; Klee, Victor; Ziegler, Günter M., eds., Convex polytopes (2nd ed.), New York & London: Springer-Verlag, ISBN 0-387-00424-6 .
• Ziegler, Günter M. (1995), Lectures on Polytopes, Graduate Texts in Mathematics, 152, Berlin, New York: Springer-Verlag .

See also

External links

• Eric W. Weisstein, Polytope at MathWorld.
• "Math will rock your world" - application of polytopes to a database of articles used to support custom news feeds via the Internet - (Business Week Online)
• Regular and semi-regular convex polytopes a short historical overview: