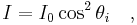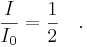Polarizer

A polarizer is a device that converts an unpolarized or mixed-polarization beam of electromagnetic waves (e.g., light) into a beam with a single polarization state (usually, a single linear polarization). Polarizers are used in many optical techniques and instruments, and polarizing filters find applications in photography and liquid crystal display technology.

Polarizers can be divided into two general categories: absorptive polarizers, where the unwanted polarization states are absorbed by the device, and beam-splitting polarizers, where the unpolarized beam is split into two beams with opposite polarization states.

Contents

Absorptive polarizers

A wire-grid polarizer converts an unpolarized beam into one with a single linear polarization. Red arrows depict the electric field vector.

The simplest polarizer in concept is the wire-grid polarizer, which consists of a regular array of fine parallel metallic wires, placed in a plane perpendicular to the incident beam. Electromagnetic waves which have a component of their electric fields aligned parallel to the wires induce the movement of electrons along the length of the wires. Since the electrons are free to move, the polarizer behaves in a similar manner as the surface of a metal when reflecting light; some energy is lost due to Joule heating in the wires, and the rest of the wave is reflected backwards along the incident beam.

For waves with electric fields perpendicular to the wires, the electrons cannot move very far across the width of each wire; therefore, little energy is lost or reflected, and the incident wave is able to travel through the grid. Since electric field components parallel to the wires are absorbed or reflected, the transmitted wave has an electric field purely in the direction perpendicular to the wires, and is thus linearly polarized. Note that the polarization direction is perpendicular to the wires; the concept that waves "slip through" the gaps between the wires is incorrect.[1]

For practical use, the separation distance between the wires must be less than the wavelength of the radiation, and the wire width should be a small fraction of this distance. This means that wire-grid polarizers are generally only used for microwaves and for far- and mid-infrared light. Using advanced lithographic techniques, very tight pitch metallic grids can be made which polarize visible light. Since the degree of polarization depends little on wavelength and angle of incidence, they are used for broad-band applications such as projection.

It is interesting to consider why there is a reflected beam, but no transmitted beam, when the symmetry of the problem suggests that the electrons in the wires should re-radiate in all directions. In simple terms the transmitted beam does "exist", but is in exact antiphase with the continuing incident beam, and so "cancels out". This, in turn, seems to contradict the idea that the incoming wave is "driving" the electrons in the wires, and so is "used up" (leaving no continued beam to cancel out the transmitted wave). In fact, if we assume that there is no heating, then no energy is used to drive the electrons — a better mental image is to think of them as "riding" on the waves that result from the interaction.

Certain crystals, due to the effects described by crystal optics, show dichroism, a preferential absorption of light which is polarized in a particular direction. They can therefore be used as polarizers. The best known crystal of this type is tourmaline. However, this crystal is seldom used as a polarizer, since the dichroic effect is strongly wavelength dependent and the crystal appears coloured. Herapathite is also dichroic, and is not strongly coloured, but is difficult to grow in large crystals.

Polaroid film was in its original form an arrangement of many microscopic herapathite crystals. Its later H-sheet form is rather similar to the wire-grid polarizer. It is made from polyvinyl alcohol (PVA) plastic with an iodine doping. Stretching of the sheet during manufacture ensures that the PVA chains are aligned in one particular direction. Electrons from the iodine dopant are able to travel along the chains, ensuring that light polarized parallel to the chains is absorbed by the sheet; light polarized perpendicularly to the chains is transmitted. The durability and practicality of Polaroid makes it the most common type of polarizer in use, for example for sunglasses, photographic filters, and liquid crystal displays. It is also much cheaper than other types of polarizer.

An important modern type of absorptive polarizer is made of elongated silver nanoparticles embedded in thin (≤0.5 mm) glass plates. These polarizers are more durable and can polarize light much better than Polaroid film, achieving polarization ratios as high as 100,000:1 and absorption of correctly-polarized light as low as 1.5%.[2] Such glass polarizers perform best for short-wavelength infrared light, and are widely used in optical fiber communications.

Beam-splitting polarizers

Beam-splitting polarizers split the incident beam into two beams of differing polarization. For an ideal polarizing beamsplitter these would be fully polarized, with orthogonal polarizations. For many common beam-splitting polarizers, however, only one of the two output beams is fully polarized. The other contains a mixture of polarization states.

Unlike absorptive polarizers, beam splitting polarizers do not need to absorb and dissipate the energy of the rejected polarization state, and so they are more suitable for use with high intensity beams such as laser light. True polarizing beamsplitters are also useful where the two polarization components are to be analyzed or used simultaneously.

Polarization by reflection

A stack of plates at Brewster's angle to a beam reflects off a fraction of the s-polarized light at each surface, leaving a p-polarized beam. Full polarization at Brewster's angle requires many more plates than shown.

When light reflects at an angle from an interface between two transparent materials, the reflectivity is different for light polarized in the plane of incidence and light polarized perpendicular to it. Light polarized in the plane is said to be p-polarized, while that polarized perpendicular to it is s-polarized. At a special angle known as Brewster's angle, no p-polarized light is reflected from the surface, thus all reflected light must be s-polarized, with an electric field perpendicular to the plane of incidence.

A simple polarizer can be made by tilting a stack of glass plates at Brewster's angle to the beam. Some of the s-polarized light is reflected from each surface of each plate. For a stack of plates, each reflection depletes the incident beam of s-polarized light, leaving a greater fraction of p-polarized light in the transmitted beam at each stage. For visible light in air and typical glass, Brewster's angle is about 57°, and about 16% of the s-polarized light present in the beam is reflected for each air-to-glass or glass-to-air transition. It takes many plates to achieve even mediocre polarization of the transmitted beam with this approach. For a stack of 10 plates (20 reflections), about 3% (= (1-0.16)20) of the s-polarized light is transmitted. The reflected beam, while fully polarized, is spread out and may not be very useful.

A more useful polarized beam can be obtained by tilting the pile of plates at a steeper angle to the incident beam. Counterintuitively, using incident angles greater than Brewster's angle yields a higher degree of polarization of the transmitted beam, at the expense of decreased overall transmission. For angles of incidence steeper than 80° the polarization of the transmitted beam can approach 100% with as few as four plates, although the transmitted intensity is very low in this case[3]. Adding more plates and reducing the angle allows a better compromise between transmission and polarization to be achieved.

Birefringent polarizers

Other polarizers exploit the birefringent properties of crystals such as quartz and calcite. In these crystals, a beam of unpolarized light incident on their surface is split by refraction into two rays. Snell's law holds for one of these rays, the ordinary or o-ray, but not for the other, the extraordinary or e-ray. In general the two rays will be in different polarization states, though not in linear polarization states except for certain propagation directions relative to the crystal axis. The two rays also experience differing refractive indices in the crystal.

A Nicol prism

A Nicol prism was an early type of birefringent polarizer, that consists of a crystal of calcite which has been split and rejoined with Canada balsam. The crystal is cut such that the o- and e-rays are in orthogonal linear polarization states. Total internal reflection of the o-ray occurs at the balsam interface, since it experiences a larger refractive index in calcite than in the balsam, and the ray is deflected to the side of the crystal. The e-ray, which sees a smaller refractive index in the calcite, is transmitted through the interface without deflection. Nicol prisms produce a very high purity of polarized light, and were extensively used in microscopy, though in modern use they have been mostly replaced with alternatives such as the Glan-Thompson prism, Glan-Foucault prism, and Glan-Taylor prism. These prisms are not true polarizing beamsplitters since only the transmitted beam is fully polarized.

A Wollaston prism

A Wollaston prism is another birefringent polarizer consisting of two triangular calcite prisms with orthogonal crystal axes that are cemented together. At the internal interface, an unpolarized beam splits into two linearly polarized rays which leave the prism at a divergence angle of 15°-45°. The Rochon and Sénarmont prisms are similar, but use different optical axis orientations in the two prisms. The Sénarmont prism is air spaced, unlike the Wollaston and Rochon prisms. These prisms truly split the beam into two fully polarized beams with perpendicular polarizations. The Nomarski prism is a variant of the Wollaston prism, which is widely used in differential interference contrast microscopy.

Thin film polarizers

This thin film polarizer dumps vertical polarization onto the floor

Thin-film polarizers are glass substrates on which a special optical coating is applied. Interference effects in the film cause them to act as beam-splitting polarizers. The substrate for the film can either be a plate, which is inserted into the beam at a particular angle, or a wedge of glass that is cemented to a second wedge to form a cube with the film cutting diagonally across the center.

Thin-film polarizers generally do not perform as well as Glan-type polarizers, but they are inexpensive and provide two beams that are about equally well polarized. The cube-type polarizers generally perform better than the plate polarizers. The former are easily confused with Glan-type birefringent polarizers.

Malus' law and other properties

Polarization of light.
In this picture, θ1 - θ0 = θi.

Malus' law, which is named after Etienne-Louis Malus, says that when a perfect polarizer is placed in a polarized beam of light, the intensity, I, of the light that passes through is given by

I = I_0 \cos^2 \theta_i \quad ,

where

I0 is the initial intensity,
and θi is the angle between the light's initial plane of polarization and the axis of the polarizer.

A beam of unpolarized light can be thought of as containing a uniform mixture of linear polarizations at all possible angles. Since the average value of 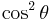\cos^2 \theta is 1/2, the transmission coefficient becomes

\frac {I}{I_0} = \frac {1}{2}\quad .

In practice, some light is lost in the polarizer and the actual transmission of unpolarized light will be somewhat lower than this, around 38% for Polaroid-type polarizers but considerably higher (>49.9%) for some birefringent prism types.

If two polarizers are placed one after another (the second polarizer is generally called an analyzer), the mutual angle between their polarizing axes gives the value of θ in Malus' law. If the two axes are orthogonal, the polarizers are crossed and in theory no light is transmitted, though again practically speaking no polarizer is perfect and the transmission is not exactly zero (for example, crossed Polaroid sheets appear slightly blue in colour). If a transparent object is placed between the crossed polarizers, any polarization effects present in the sample (such as birefringence) will be shown as increases in transmission. This effect is used in polarimetry to measure the optical activity of a sample.

Real polarizers are also not perfect blockers of the polarization orthogonal to their polarization axis; the ratio of the transmission of the unwanted component to the wanted component is called the extinction ratio, and varies from around 1:500 for Polaroid to about 1:106 for Glan-Taylor prism polarizers.

See also

Notes and references

  1. ↑ Ahn, S. W.; K. D. Lee, J. S. Kim, S. H. Kim, J. D. Park, S. H. Lee, P. W. Yoon (2005). "Fabrication of a 50 nm half-pitch wire grid polarizer using nanoimprint lithography". Nanotechnology 16 (9): 1874–1877. doi:10.1088/0957-4484/16/9/076. 
  2. ↑ "Polarcor glass polarizers: Product information" (pdf). Corning.com (December 2006). Retrieved on 2008-08-08.
  3. ↑ Collett, Edward. Field Guide to Polarization, SPIE Field Guides vol. FG05, SPIE (2005) ISBN 0-8194-5868-6.