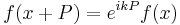Periodic function
In mathematics, a periodic function is a function that repeats its values after some definite period has been added to its independent variable. This property is called periodicity.

Contents |
Examples
Everyday examples are seen when the variable is time; for instance the hands of a clock or the phases of the moon show periodic behaviour. Periodic motion is motion in which the position(s) of the system are expressible as periodic functions, all with the same period.
For a function on the real numbers or on the integers, that means that the entire graph can be formed from copies of one particular portion, repeated at regular intervals.
Definition
A function f in domain  is called periodic, if there exist number
is called periodic, if there exist number 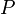 , different from zero, such that
, different from zero, such that
- f(x + P) = f(x)
for all values of x in the domain  . In this case, number P is called the period of the function f in the domain
. In this case, number P is called the period of the function f in the domain  .
.
In general, period P has no need to be real (it may be a complex number). For example the exponential has period 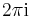 .
.
Aperiodic function
An aperiodic function (non-periodic function) is one that has no such period P (not to be confused with an antiperiodic function (below) for which f(x + P) = −f(x) for some P).
Properties of period
If a function f is periodic with period P, then for all x in the domain of f and all integers n,
- f(x + nP) = f(x).

More examples
A simple example of a periodic function is the function f that gives the "fractional part" of its argument. Its period is 1. In particular,
- f( 0.5 ) = f( 1.5 ) = f( 2.5 ) = ... = 0.5.
The graph of the function f is the sawtooth wave.
The trigonometric functions sine and cosine are common periodic functions, with period 2π (see the figure on the right). The subject of Fourier series investigates the idea that an 'arbitrary' periodic function is a sum of trigonometric functions with matching periods.
According to the definition above, some exotic functions, for example the Dirichlet function, are also periodic; in the case of Dirichlet function, any rational number is periodic.
Double-periodic functions
A function whose domain is the complex numbers can have two incommensurate periods without being constant. The elliptic functions are such functions. ("Incommensurate" in this context means not real multiples of each other.)
Properties
if f(x) is a function with period P, then f(ax), where a is a positive constant, is periodic with period P/a. For example, f(x)=sinx has period 2π, therefore sin(5x) will have period 2π/5.
Antiperiodic functions and other generalizations
One common generalization of periodic functions is that of antiperiodic functions. This is a function f such that f(x + P) = −f(x) for all x. (Thus, a P-antiperiodic function is a 2P-periodic function.)
A further generalization appears in the context of Bloch waves and Floquet theory, which govern the solution of various periodic differential equations. In this context, the solution (in one dimension) is typically a function of the form:
where k is a real or complex number (the Bloch wavevector or Floquet exponent). Functions of this form are sometimes called Bloch-periodic in this context. A periodic function is the special case k = 0, and an antiperiodic function is the special case k = π/P.
Periodic sequences
Some naturally-occurring sequences are periodic, for example (eventually) the decimal expansion of any rational number (see recurring decimal). We can therefore speak of the period or period length of a sequence. This is (if one insists) just a special case of the general definition.
Periodic mapping
A mapping f of a set into itself is said to be periodic if some iterate fn is the identity mapping for some integer n > 1; the smallest possible n is called the period of f. This concept is commonly used in the theory of dynamical systems.
Translational symmetry
If a function is used to describe an object, e.g. an infinite image is given by the color as function of position, the periodicity of the function corresponds to translational symmetry of the object.
Cycle
The restriction of a periodic function to an interval whose length is equal to the period is called a cycle.
See also
- Almost periodic function
- Amplitude
- Definite pitch
- Doubly-periodic function
- Frequency
- Oscillation
- Quasiperiodic function
- Wavelength