Perfect number
| Divisibility-based sets of integers |
| Form of factorization: |
| Prime number |
| Composite number |
| Powerful number |
| Square-free number |
| Achilles number |
| Constrained divisor sums: |
| Perfect number |
| Almost perfect number |
| Quasiperfect number |
| Multiply perfect number |
| Hyperperfect number |
| Superperfect number |
| Unitary perfect number |
| Semiperfect number |
| Primitive semiperfect number |
| Practical number |
| Numbers with many divisors: |
| Abundant number |
| Highly abundant number |
| Superabundant number |
| Colossally abundant number |
| Highly composite number |
| Superior highly composite number |
| Other: |
| Deficient number |
| Weird number |
| Amicable number |
| Friendly number |
| Sociable number |
| Solitary number |
| Sublime number |
| Harmonic divisor number |
| Frugal number |
| Equidigital number |
| Extravagant number |
| See also: |
| Divisor function |
| Divisor |
| Prime factor |
| Factorization |
In mathematics, a perfect number is defined as a positive integer which is the sum of its proper positive divisors, that is, the sum of the positive divisors excluding the number itself. Equivalently, a perfect number is a number that is half the sum of all of its positive divisors (including itself), or σ(n) = 2n.
The first perfect number is 6, because 1, 2, and 3 are its proper positive divisors, and 1 + 2 + 3 = 6. Equivalently, the number 6 is equal to half the sum of all its positive divisors: ( 1 + 2 + 3 + 6 ) / 2 = 6.
The next perfect number is 28 = 1 + 2 + 4 + 7 + 14. This is followed by the perfect numbers 496 and 8128 (sequence A000396 in OEIS).
These first four perfect numbers were the only ones known to early Greek mathematics.
Contents |
Even perfect numbers
Euclid discovered that the first four perfect numbers are generated by the formula 2n−1(2n − 1):
- for n = 2: 21(22 − 1) = 6
- for n = 3: 22(23 − 1) = 28
- for n = 5: 24(25 − 1) = 496
- for n = 7: 26(27 − 1) = 8128.
Noticing that 2n − 1 is a prime number in each instance, Euclid proved that the formula 2n−1(2n − 1) gives an even perfect number whenever 2n − 1 is prime (Euclid, Prop. IX.36).
Ancient mathematicians made many assumptions about perfect numbers based on the four they knew, but most of those assumptions would later prove to be incorrect. One of these assumptions was that since 2, 3, 5, and 7 are precisely the first four primes, the fifth perfect number would be obtained when n = 11, the fifth prime. However, 211 − 1 = 2047 = 23 × 89 is not prime and therefore n = 11 does not yield a perfect number. Two other wrong assumptions were:
- The fifth perfect number would have five digits in base 10 since the first four had 1, 2, 3, and 4 digits respectively.
- The perfect numbers' final digits would go 6, 8, 6, 8, alternately.
The fifth perfect number (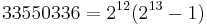 ) has 8 digits, thus refuting the first assumption. For the second assumption, the fifth perfect number indeed ends with a 6. However, the sixth (8 589 869 056) also ends in a 6. It is straightforward to show that the last digit of any even perfect number must be 6 or 8.
) has 8 digits, thus refuting the first assumption. For the second assumption, the fifth perfect number indeed ends with a 6. However, the sixth (8 589 869 056) also ends in a 6. It is straightforward to show that the last digit of any even perfect number must be 6 or 8.
In order for 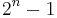 to be prime, it is necessary but not sufficient that
to be prime, it is necessary but not sufficient that 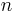 should be prime. Prime numbers of the form 2n − 1 are known as Mersenne primes, after the seventeenth-century monk Marin Mersenne, who studied number theory and perfect numbers.
should be prime. Prime numbers of the form 2n − 1 are known as Mersenne primes, after the seventeenth-century monk Marin Mersenne, who studied number theory and perfect numbers.
Over a millennium after Euclid, Ibn al-Haytham (Alhazen) circa 1000 AD realized that every even perfect number is of the form 2n−1(2n − 1) where 2n − 1 is prime, but he was not able to prove this result.[1] It was not until the 18th century that Leonhard Euler proved that the formula 2n−1(2n − 1) will yield all the even perfect numbers. Thus, there is a concrete one-to-one association between even perfect numbers and Mersenne primes. This result is often referred to as the Euclid-Euler Theorem. As of September 2008, only 46 Mersenne primes are known,[2] which means there are 46 perfect numbers known, the largest being 243,112,608 × (243,112,609 − 1) with 25,956,377 digits.
The first 39 even perfect numbers are 2n−1(2n − 1) for
- n = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917 (sequence A000043 in OEIS).
The other 7 known are for n = 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 43112609. It is not known whether there are others between them.
It is still uncertain whether there are infinitely many Mersenne primes and perfect numbers. The search for new Mersenne primes is the goal of the GIMPS distributed computing project.
Since any even perfect number has the form 2n−1(2n − 1), it is a triangular number, and, like all triangular numbers, it is the sum of all natural numbers up to a certain point; in this case: 2n − 1. Furthermore, any even perfect number except the first one is the sum of the first 2(n−1)/2 odd cubes:
Even perfect numbers (except 6) give remainder 1 when divided by 9. This can be reformulated as follows. Adding the digits of any even perfect number (except 6), then adding the digits of the resulting number, and repeating this process until a single digit is obtained—the resulting number is called the digital root—produces the number 1. For example, the digital root of 8128 = 1, since 8 + 1 + 2 + 8 = 19, 1 + 9 = 10, and 1 + 0 = 1.
Odd perfect numbers
It is unknown whether there are any odd perfect numbers. Various results have been obtained, but none that has helped to locate one or otherwise resolve the question of their existence. Carl Pomerance has presented a heuristic argument which suggests that no odd perfect numbers exist.[3] Also, it has been conjectured that there are no odd Ore's harmonic numbers (except for 1). If true, this would imply that there are no odd perfect numbers.
Any odd perfect number N must satisfy the following conditions:
- N > 10300. A search is currently on to prove that N > 10500. [4]
- N is of the form
-
- where:
- The largest prime factor of N is greater than 108 (Takeshi Goto and Yasuo Ohno, 2006).
- The second largest prime factor is greater than 104, and the third largest prime factor is greater than 100 (Iannucci 1999, 2000).
- N has at least 75 prime factors and at least 9 distinct prime factors. If 3 is not one of the factors of N, then N has at least 12 distinct prime factors (Nielsen 2006; Kevin Hare 2005).
- When
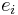 ≤ 2 for every i
≤ 2 for every i
- The smallest prime factor of N is at least 739 (Cohen 1987).
- α ≡ 1 (mod 12) or α ≡ 9 (mod 12) (McDaniel 1970).
In 1888, Sylvester stated:
…a prolonged meditation on the subject has satisfied me that the existence of any one such [odd perfect number]—its
escape, so to say, from the complex web of conditions which hem it in on all sides—would be little short of a miracle.—[5]
Minor results
Even perfect numbers have a very precise form; odd perfect numbers are rare, if indeed they do exist. There are a number of results on perfect numbers that are actually quite easy to prove but nevertheless superficially impressive; some of them also come under Richard Guy's strong law of small numbers:
- An odd perfect number is not divisible by 105 (Kühnel 1949).
- Every odd perfect number is of the form 12m + 1 or 324m + 81 or 468m + 117 (Roberts 2008).
- The only even perfect number of the form
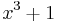 is 28 (Makowski 1962).
is 28 (Makowski 1962). - A Fermat number cannot be a perfect number (Luca 2000).
- The reciprocals of the divisors of a perfect number N must add up to 2:
- For 6, we have
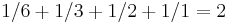 ;
; - For 28, we have
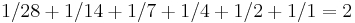 , etc.
, etc.
- For 6, we have
- The number of divisors of a perfect number (whether even or odd) must be even, since N cannot be a perfect square.
- From these two results it follows that every perfect number is an Ore's harmonic number.
Related concepts
The sum of proper divisors gives various other kinds of numbers. Numbers where the sum is less than the number itself are called deficient, and where it is greater than the number, abundant. These terms, together with perfect itself, come from Greek numerology. A pair of numbers which are the sum of each other's proper divisors are called amicable, and larger cycles of numbers are called sociable. A positive integer such that every smaller positive integer is a sum of distinct divisors of it is a practical number.
By definition, a perfect number is a fixed point of the restricted divisor function s(n) = σ(n) − n, and the aliquot sequence associated with a perfect number is a constant sequence.
See also
- Perfection
Notes
- ↑ O'Connor, John J.; Robertson, Edmund F., "Abu Ali al-Hasan ibn al-Haytham", MacTutor History of Mathematics archive
- ↑ http://www.mersenne.org/
- ↑ Oddperfect.org
- ↑ Oddperfect.org
- ↑ The Collected Mathematical Papers of James Joseph Sylvester p. 590, tr. from "Sur les nombres dits de Hamilton", Compte Rendu de l'Assoiation Française (Toulouse, 1887), pp. 164–168.
References
- Graeme L. Cohen, "On the largest component of an odd perfect number", Journal of the Australian Mathematical Society, 42:2 (1987), pp. 280–286.
- Euclid, Elements, Book IX, Proposition 36. See D.E. Joyce's website for a translation and discussion of this proposition and its proof.
- Takeshi Goto and Yasuo Ohno, "Odd perfect numbers have a prime factor exceeding 108", Mathematics of Computation, in press, 2008. doi:10.1090/S0025-5718-08-02050-9.
- Otto Grün, "Über ungerade vollkommene Zahlen", Mathematische Zeitschrift, 55 (1952), pp. 353–354.
- Kevin Hare, New techniques for bounds on the total number of prime factors of an odd perfect number. Preprint, 2005. Available from his webpage.
- Douglas E. Iannucci, "The second largest prime divisor of an odd perfect number exceeds ten thousand", Mathematics of Computation, 68:228 (1999), pp. 1749–1760.
- Douglas E. Iannucci, "The third largest prime divisor of an odd perfect number exceeds one hundred", Mathematics of Computation, 69:230 (2000), pp. 867–879.
- H.-J. Kanold, "Untersuchungen über ungerade vollkommene Zahlen", Journal für die Reine und Angewandte Mathematik, 183 (1941), pp. 98–109.
- Ullrich Kühnel, "Verschärfung der notwendigen Bedingungen für die Existenz von ungeraden vollkommenen Zahlen", Mathematische Zeitschrift, 52 (1949), pp. 201—211.
- Florian Luca, "The anti-social Fermat number", Amer. Math. Monthly, 107 (2000), pp. 171–173.
- W. L. McDaniel, "The non-existence of odd perfect numbers of a certain form", Archiv der Mathematik (Basel), 21 (1970), pp. 52–53.
- Pace P. Nielsen, "An upper bound for odd perfect numbers," Integers, 3 (2003), A14, 9 pp.
- Pace P. Nielsen, "Odd perfect numbers have at least nine different prime factors", Mathematics of Computation, in press, 2006. arΧiv:math.NT/0602485.
- T. Roberts, "On the Form of an Odd Perfect Number", Australian Mathematical Gazette, 35:4 (2008), p244.
- R. Steuerwald, "Verschärfung einer notwendigen Bedingung für die Existenz einer ungeraden vollkommenen Zahl", S.-B. Bayer. Akad. Wiss., 1937, pp. 69–72.
- Tomohiro Yamada, "Odd perfect numbers of a special form", Colloq. Math., 103 (2005), pp. 303–307.
External links
- David Moews: Perfect, amicable and sociable numbers
- Perfect numbers - History and Theory
- Eric W. Weisstein, perfect number at MathWorld.
- A000396: List of perfect numbers
- OddPerfect.org A projected distributed computing project to search for odd perfect numbers
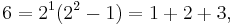
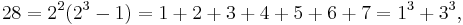
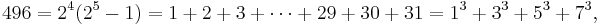
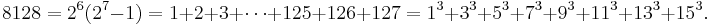
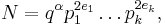
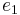 ≡
≡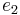 ≡...≡
≡...≡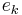 ≡ 1 (
≡ 1 (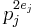 > 1020 for some j (Cohen 1987).
> 1020 for some j (Cohen 1987).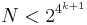 (Nielsen 2003).
(Nielsen 2003).