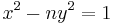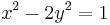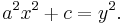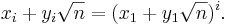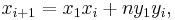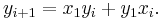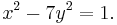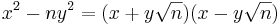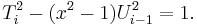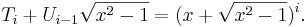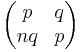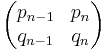Pell's equation

Pell's equation is any Diophantine equation of the form

x^2-ny^2=1\,

where n is a nonsquare integer and x and y are integers. Trivially, x = 1 and y = 0 always solve this equation. Lagrange proved that for any natural number n that is not a perfect square there are x and y > 0 that satisfy Pell's equation. Moreover, infinitely many such solutions of this equation exist. These solutions yield good rational approximations of the form x/y  to the square root of n.

The name of this equation arose from Leonhard Euler's mistakenly attributing its study to John Pell. Euler was aware of the work of Lord Brouncker, the first European mathematician to find a general solution of the equation, but apparently confused Brouncker with Pell. This equation was first studied extensively in India, starting with Brahmagupta, who developed the chakravala method to solve Pell's equation and other quadratic indeterminate equations in his Brahma Sphuta Siddhanta in 628, about a thousand years before Pell's time. His Brahma Sphuta Siddhanta was translated into Arabic in 773 and was subsequently translated into Latin in 1126. Bhaskara II in the 12th century and Narayana in the 14th century both found general solutions to Pell's equation and other quadratic indeterminate equations. Solutions to specific examples of the Pell equation, such as the Pell numbers arising from the equation with n = 2, had been known for much longer, since the time of Pythagoras in Greece and to a similar date in India.

For a more detailed discussion of much of the material here, see Lenstra (2002) and Barbeau (2003).

Contents

History

Pell's equations were studied as early as 400 BC in India and Greece. They were mainly interested in the equation

x^2 - 2y^2=1 \,

because of its connection to the square root of two. Indeed, if x and y are integers satisfying this equation, then x / y is an approximation of √2. For example, Baudhayana discovered that x = 17, y = 12 and x = 577, y = 408 are two solutions to the Pell equation, and give very close approximations to the square root of two.

Later, Archimedes used a similar equation to approximate the square root of 3, and found 1351/780.

Around AD 250, Diophantus created a different form of the Pell equation

a^2 x^2+c=y^2. \,

He solved this equation for a = 1, and c = −1, 1, and 12, and also solved for a = 3 and c = 9.

Brahmagupta created a general way to solve Pell's equation known as the chakravala method. Alkarkhi worked on similar problems to Diophantus, and Bháscara Achárya created a way to create new solutions to Pell equations from one solution. E. Strachey published the work of Bháscara into English in 1813.

The general theory of Pell's equation, based on continued fractions and algebraic manipulations with numbers of the form 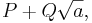P+Q\sqrt{a}, was developed by Lagrange in 1766–1769.[1]

Solution technique

Let 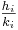\tfrac{h_i}{k_i} denote the sequence of convergents to the continued fraction for 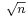\scriptstyle\sqrt{n}. Then the pair (x1,y1) solving Pell's equation and minimizing x satisfies x1 = hi and y1 = ki for some i. This pair is called the fundamental solution. Thus, the fundamental solution may be found by performing the continued fraction expansion and testing each successive convergent until a solution to Pell's equation is found.

Once the fundamental solution is found, all remaining solutions may be calculated algebraically as

x_i + y_i\sqrt n = (x_1 + y_1\sqrt n)^i.

Equivalently, we may calculate subsequent solutions via the recurrence relations

\displaystyle x_{i+1} = x_1 x_i + n y_1 y_i,
\displaystyle y_{i+1} = x_1 y_i + y_1 x_i.

Example

As an example, consider the instance of Pell's equation for n = 7; that is,

\displaystyle x^2 - 7 y^2 = 1.

The sequence of convergents for the square root of seven are

h / k (Convergent) h2 −7k2 (Pell-type approximation)
2 / 1 −3
3 / 1 +2
5 / 2 −3
8 / 3 +1

Therefore, the fundamental solution is formed by the pair (8, 3). Applying the recurrence formula to this solution generates the infinite sequence of solutions

(8, 3); (127, 48); (2024, 765); (32257, 12192); (514088, 194307); (8193151; 3096720); (130576328, 49353213); ...

Connection to algebraic number theory

Pell's equation is closely related to the theory of algebraic numbers, as the formula

x^2 - n y^2 = (x + y\sqrt n)(x - y\sqrt n)

is the norm for the ring ℤ[√n] and for the closely related quadratic field ℚ(√n). Thus, a pair of integers (x,y) solves Pell's equation if and only if x + y√n is a unit with norm 1 in ℤ[√n]. Dirichlet's unit theorem, that all units of ℤ[√n] can be expressed as powers of a single fundamental unit (and multiplication by a sign), is an algebraic restatement of the fact that all solutions to the Pell equation can be generated from the fundamental solution. The fundamental unit can in general be found by solving a Pell-like equation but it does not always correspond directly to the fundamental solution of Pell's equation itself.

Connection to Chebyshev polynomials

Demeyer (2007) mentions a connection between Pell's equation and the Chebyshev polynomials: If Ti (x) and Ui (x) are the Chebyshev polynomials of the first and second kind, respectively, then these polynomials satisfy a form of Pell's equation in any polynomial ring R[x], with n = x² − 1:

T_i^2 - (x^2-1) U_{i-1}^2 = 1.

Thus, these polynomials can be generated by the standard technique for Pell equations of taking powers of a fundamental solution:

T_i + U_{i-1} \sqrt{x^2-1} = (x + \sqrt{x^2-1})^i.

It may further be observed that, if (xi,yi) are the solutions to any integer Pell equation, then xi = Ti (x1) and yi = y1Ui − 1(x1) (Barbeau, chapter 3).

Pell's equation and continued fractions

A general development of solutions of Pell's equation in terms of continued fractions can be presented, as the solutions x and y are approximates to the square root of n and thus are a special case of continued fraction approximations for quadratic irrationals. Gauss classified such solutions into 64 or 65 sets, with the precise classification of one or the other implying the truth or falsity of the Riemann hypothesis.

The relationship to the continued fractions implies that the solutions to Pell's equation form a semigroup subset of the modular group. Thus, for example, if p and q satisfy Pell's equation, then

\begin{pmatrix} p & q \\ nq & p \end{pmatrix}

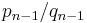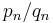is a matrix of unit determinant. Products of such matrices take exactly the same form, and thus all such products yield solutions to Pell's equation. This can be understood in part to arise from the fact that successive convergents of a continued fraction share the same property: If p_{n-1}/q_{n-1} and p_{n}/q_{n} are two successive convergents of a continued fraction, then the matrix

\begin{pmatrix} p_{n-1} & p_{n} \\ q_{n-1} & q_{n} \end{pmatrix}

has determinant (−1)n.

Størmer's theorem applies Pell equations to find pairs of consecutive smooth numbers. As part of this theory, Størmer also investigated divisibility relations among solutions to Pell's equation; in particular, he showed that each solution other than the fundamental solution has a prime factor that does not divide n.

As Lenstra (2002) describes, Pell's equation can also be used to solve Archimedes' cattle problem.

Notes

  1. ↑ Solution d'un Probleme d'Arithmetique, in Oeveres, t.1, 671–732

An analogous equation, known as the Negative Pell equation has also been extensively studied and can be solved via a method of using continued fractions. However, unlike the Pell equation, we do not know the exact time for which the Negative Pell equation is soluble. A recent paper by Cremona and Odoni has demonstrated that the proportion of square-free ds, for which the Pell equation is soluble is at least 40% (approximately).

References

External links