Connected space

In topology and related branches of mathematics, a connected space is a topological space which cannot be represented as the disjoint union of two or more nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces. A stronger notion is that of a path-connected space, which is a space where any two points can be joined by a path.
A subset of a topological space X is a connected set if it is a connected space when viewed as a subspace of X.
It is usually easy to think about what is not connected. A simple example would be a space consisting of two rectangles, each of which is a space and not adjoined to the other. The space is not connected since two rectangles are disjoint. Another good example is a space with an annulus removed. The space is not connected since you cannot connect two points, one inside the annulus and the other outside; hence the term "connect".
Contents |
Formal definition
A topological space X is said to be disconnected if it is the union of two disjoint nonempty open sets. Otherwise, X is said to be connected. A subset of a topological space is said to be connected if it is connected under its subspace topology. Some authors specifically exclude the empty set with its unique topology as a connected space, but this encyclopedia does not follow that practice.
For a topological space X the following conditions are equivalent:
- X is connected.
- X cannot be divided into two disjoint nonempty closed sets.
- The only subsets of X which are both open and closed (clopen sets) are X and the empty set.
- The only subsets of X with empty boundary are X and the empty set.
- X cannot be written as the union of two nonempty separated sets.
- The only continuous functions from X to {0,1} are constant.
The maximal connected subsets of any topological space are called the connected components of the space. The components form a partition of the space (that is, they are disjoint and their union is the whole space). Every component is a closed subset of the original space. The components in general need not be open: the components of the rational numbers, for instance, are the one-point sets. A space in which all components are one-point sets is called totally disconnected. Related to this property, a space X is called totally separated if, for any two elements x and y of X, there exist disjoint open neighborhoods U of x and V of y such that X is the union of U and V. Clearly any totally separated space is totally disconnected, but the converse does not hold. For example take two copies of the rational numbers Q, and identify them at every point except zero. The resulting space, with the quotient topology, is totally disconnected. However, by considering the two copies of zero, one sees that the space is not totally separated. In fact, it is not even Hausdorff, and the condition of being totally separated is strictly stronger than the condition of being Hausdorff.
Examples
- The closed interval [0, 2] in the standard subspace topology is connected; although it can, for example, be written as the union of [0, 1) and [1, 2], the second set is not open in the aforementioned topology of [0, 2].
- The union of [0, 1) and (1, 2] is disconnected; both of these intervals are open in the standard topological space [0, 1) ∪ (1, 2].
- (0, 1) ∪ {3} is disconnected.
- A convex set is connected; it is actually simply connected.
- A Euclidean plane excluding the origin, (0, 0), is connected, but is not simply connected. The three-dimensional Euclidean space without the origin is connected, and even simply connected. In contrast, the one-dimensional Euclidean space without the origin is not connected.
- A Euclidean plane with a straight-line removed is not connected since it consists of two half-planes.
- The space of real numbers with the usual topology is connected.
- Any topological vector space over a connected field is connected.
- Every discrete topological space with at least two elements is disconnected, in fact such a space is totally disconnected.
- The Cantor set is totally disconnected; since the set contains uncountably many points, it has uncountably many components.
- If a space X is homotopic to a connected space, then X is itself connected.
- The topologist's sine curve is an example of a set that is connected but is neither path connected nor locally connected.
Path connectedness

The space X is said to be path-connected (or pathwise connected or 0-connected) if for any two points x and y in X there exists a continuous function f from the unit interval [0,1] to X with f(0) = x and f(1) = y. (This function is called a path from x to y.)
Every path-connected space is connected. The reverse is not always true: examples of connected spaces that are not path-connected include the extended long line L* and the topologist's sine curve.
However, subsets of the real line R are connected if and only if they are path-connected; these subsets are the intervals of R. Also, open subsets of Rn or Cn are connected if and only if they are path-connected. Additionally, connectedness and path-connectedness are the same for finite topological spaces.
A space X is said to be arc-connected or arcwise connected if any two distinct points can be joined by an arc, that is a path f which is a homeomorphism between the unit interval [0, 1] and its image f([0, 1]). It can be shown any Hausdorff space which is path-connected is also arc-connected. An example of a space which is path-connected but not arc-connected is provided by adding a second copy 0' of 0 to the nonnegative real numbers [0, ∞). One endows this set with a partial order by specifying that 0'<a for any positive number a, but leaving 0 and 0' incomparable. One then endows this set with the order topology, that is one takes the open intervals (a, b) = {x | a < x < b} and the half-open intervals [0, a) = {x | 0 ≤ x < a}, [0', a) = {x | 0' ≤ x < a} as a base for the topology. The resulting space is a T1 space but not a Hausdorff space. Clearly 0 and 0' can be connected by a path but not by an arc in this space.
Local connectedness
A topological space is said to be locally connected at a point x if every neighbourhood of x contains a connected open neighbourhood. It is locally connected if it has a base of connected sets. It can be shown that a space X is locally connected if and only if every component of every open set of X is open. The topologist's sine curve is an example of a connected space that is not locally connected.
Similarly, a topological space is said to be locally path-connected if it has a base of path-connected sets. An open subset of a locally path-connected space is connected if and only if it is path-connected. This generalizes the earlier statement about Rn and Cn, each of which is locally path-connected. More generally, any topological manifold is locally path-connected.
Theorems
- Main theorem: Let X and Y be topological spaces and let f : X → Y be a continuous function. If X is (path-)connected then the image f(X) is (path-)connected. This result can be considered a generalization of the intermediate value theorem.
- If
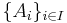 is a family of connected subsets of a topological space X indexed by an arbitrary set
is a family of connected subsets of a topological space X indexed by an arbitrary set 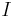 such that for all
such that for all 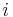 ,
,  in
in 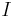 ,
, 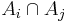 is nonempty, then
is nonempty, then 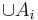 is also connected.
is also connected. - If
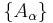 is a nonempty family of connected subsets of a topological space X such that
is a nonempty family of connected subsets of a topological space X such that 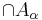 is nonempty, then
is nonempty, then 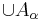 is also connected.
is also connected. - Every path-connected space is connected.
- Every locally path-connected space is locally connected.
- A locally path-connected space is path-connected if and only if it is connected.
- The closure of a connected subset is connected.
- The connected components are always closed (but in general not open)
- The connected components of a locally connected space are also open.
- The connected components of a space are disjoint unions of the path-connected components (which in general are neither open nor closed).
- Every quotient of a connected (resp. path-connected) space is connected (resp. path-connected).
- Every product of a family of connected (resp. path-connected) spaces is connected (resp. path-connected).
- Every open subset of a locally connected (resp. locally path-connected) space is locally connected (resp. locally path-connected).
- Every manifold is locally path-connected.
Graphs
Graphs have path connected subsets, namely those subsets for which every pair of points has a path of edges joining them. But it is not always possible to find a topology on the set of points which induces the same connected sets. The 5-cycle graph (and any n-cycle with n>3 odd) is one such example.
As a consequence, a notion of connectedness can be formulated independently of the topology on a space. To wit, there is a category of connective spaces consisting of sets with collections of connected subsets satisfying connectivity axioms; their morphisms are those functions which map connected sets to connected sets (Muscat & Buhagiar 2006). Topological spaces and graphs are special cases of connective spaces; indeed, the finite connective spaces are precisely the finite graphs.
However, it is possible to embed a graph into  such that the edges are homeomorphic to copies of the closed unit interval [0,1]. Then one can show that the graph is connected (in the graph theoretical sense) if and only if this subset of
such that the edges are homeomorphic to copies of the closed unit interval [0,1]. Then one can show that the graph is connected (in the graph theoretical sense) if and only if this subset of  is connected w.r.t. the subspace topology.
is connected w.r.t. the subspace topology.
See also
- locally connected space
- uniformly connected space
- connected component (graph theory)
- simply connected space
- n-connected
- hyperconnected space
- Connectedness locus
References
- Munkres, James R. (2000). Topology, Second Edition. Prentice Hall. ISBN 0-13-181629-2.
- Eric W. Weisstein, Connected Set at MathWorld.
- V. I. Malykhin (2001), "Connected space", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- Muscat, J; Buhagiar, D (2006), "Connective Spaces", Mem. Fac. Sci. Eng. Shimane Univ., Series B: Math. Sc. 39: 1–13, http://www.math.shimane-u.ac.jp/common/memoir/39/D.Buhagiar.pdf.