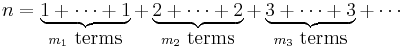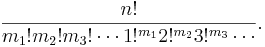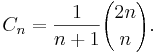Partition of a set

A partition of a set into 6 parts: an Euler diagram representation.

In mathematics, a partition of a set X is a division of X into non-overlapping "parts" or "blocks" or "cells" that cover all of X. More formally, these "cells" are both collectively exhaustive and mutually exclusive with respect to the set being partitioned.

1 Definition
2 Examples
3 Partitions and equivalence relations
4 Partial ordering of the lattice of partitions
5 Noncrossing partitions
6 The number of partitions
7 See also
8 Notes
9 References

Definition

A partition of a set X is a set of nonempty subsets of X such that every element x in X is in exactly one of these subsets.

Equivalently, a set P of nonempty sets is a partition of X if

The union of the elements of P is equal to X. (We say the elements of P cover X.)
The intersection of any two elements of P is empty. (We say the elements of P are pairwise disjoint.)

In mathematical notation, these two conditions can be written as

$\bigcup P = X$
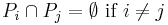$P_i \cap P_j =\emptyset \text{ if } i \neq j$ .

The elements of P are sometimes called the blocks or parts of the partition.^[1]

Examples

Every singleton set {x} has exactly one partition, namely { {x} }.
For any nonempty set X, P = {X} is a partition of X.
For any non-empty proper subset A of a set U, this A together with its complement is a partition of U.
The set { 1, 2, 3 } has these five partitions.
- { {1}, {2}, {3} }, sometimes denoted by 1/2/3.
- { {1, 2}, {3} }, sometimes denoted by 12/3.
- { {1, 3}, {2} }, sometimes denoted by 13/2.
- { {1}, {2, 3} }, sometimes denoted by 1/23.
- { {1, 2, 3} }, sometimes denoted by 123.
Note that
- { {}, {1,3}, {2} } is not a partition (because it contains the empty set).
- { {1,2}, {2, 3} } is not a partition (of any set) because the element 2 is contained in more than one distinct subset.
- { {1}, {2} } is not a partition of {1, 2, 3} because none of its blocks contains 3; however, it is a partition of {1, 2}.

Partitions and equivalence relations

If an equivalence relation is given on the set X, then the set of all equivalence classes forms a partition of X. Conversely, if a partition P is given on X, we can define an equivalence relation on X by writing x ~ y if there exists a member of P which contains both x and y. The notions of "equivalence relation" and "partition" are thus essentially equivalent.^[2]

Partial ordering of the lattice of partitions

Given two partitions π and ρ of a given set X, we say that π is finer than ρ, or, equivalently, that ρ is coarser than π, if π splits the set X into smaller blocks than ρ does, i.e. if every element of π is a subset of some element of ρ. In that case, one writes π ≤ ρ.

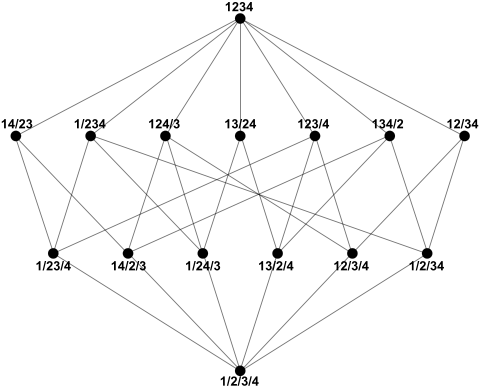
The relation of "being-finer-than" is a partial order on the set of all partitions of the set X, and indeed even a complete lattice. In case n = 4, the partial order of the set of all 15 partitions is depicted in this Hasse diagram:

Noncrossing partitions

The lattice of noncrossing partitions of a finite set has recently taken on importance because of its role in free probability theory. These form a subset of the lattice of all partitions, but not a sublattice, since the join operations of the two lattices do not agree.

The number of partitions

The Bell number B_n, named in honor of Eric Temple Bell, is the number of different partitions of a set with n elements. The first several Bell numbers are B₀ = 1, B₁ = 1, B₂ = 2, B₃ = 5, B₄ = 15, B₅ = 52, B₆ = 203.

The exponential generating function for Bell numbers is

$\sum_{n=0}^\infty\frac{B_n}{n!}z^n=e^{e^z-1}.$

Bell numbers satisfy the recursion $B_{n+1}=\sum_{k=0}^n {n\choose k}B_k.$

The Stirling number of the second kind S(n, k) is the number of partitions of a set of size n into k blocks.

The number of partitions of a set of size n corresponding to the integer partition

$n=\underbrace{1+\cdots+1}_{m_1\ \mbox{terms}} +\underbrace{2+\cdots+2}_{m_2\ \mbox{terms}} +\underbrace{3+\cdots+3}_{m_3\ \mbox{terms}}+\cdots$

of n is the Faà di Bruno coefficient

${n! \over m_1!m_2!m_3!\cdots 1!^{m_1}2!^{m_2}3!^{m_3}\cdots}.$

The number of noncrossing partitions of a set of size n is the nth Catalan number, given by

$C_n={1 \over n+1}{2n \choose n}.$

Notes

↑ Brualdi, pp. 44-45
↑ Schechter, p. 54

References

Brualdi, Richard A. (2004). Introductory Combinatorics (4th edition ed.). Pearson Prentice Hall. ISBN 0131001191.
Schechter, Eric (1997). Handbook of Analysis and Its Foundations. Academic Press. ISBN 0126227608.