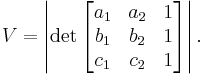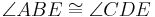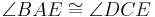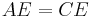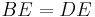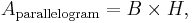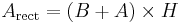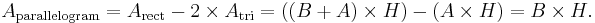Parallelogram

In geometry, a parallelogram is a quadrilateral with two sets of parallel sides. The opposite sides of a parallelogram are of equal length, and the opposite angles of a parallelogram are congruent. The three-dimensional counterpart of a parallelogram is a parallelepiped.
Contents |
Properties
- The area,
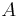 , of a parallelogram is
, of a parallelogram is 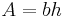 , where
, where 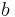 is the base of the parallelogram and
is the base of the parallelogram and 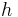 is its height.
is its height. - The area of a parallelogram is twice the area of a triangle created by one of its diagonals.
- The area of a parallelogram is also equal to the magnitude of the vector cross product of two adjacent sides.
- The diagonals of a parallelogram bisect each other.
- Opposite sides of a parallelogram are equal.
- Opposite angles of a parallelogram are equal.
- Each diagonal bisects the parallelogram into two congruent triangles.
- It is possible to create a tessellation of a plane with any parallelogram.
The properties of having equal opposite sides and opposite angles are shared with the antiparallelogram, a type of non-convex quadrilateral in which the two longer edges cross each other.
Computing the area of a parallelogram
Let  and let
and let ![V=[a\ b]\in\R^{2\times2}](/2009-wikipedia_en_wp1-0.7_2009-05/I/d4a4d61871d9369ef09c27599408398c.png) denote the matrix with columns
denote the matrix with columns  and
and 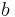 . Then the area of the parallelogram generated by
. Then the area of the parallelogram generated by  and
and 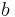 is equal to
is equal to 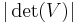
Let 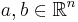 and let
and let ![V=[a\ b]\in\R^{n\times2}](/2009-wikipedia_en_wp1-0.7_2009-05/I/7ee63da52bc6cdd0d3bb9d38d1870354.png) . Then the area of the parallelogram generated by
. Then the area of the parallelogram generated by  and
and 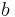 is equal to
is equal to 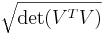
Let 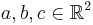 . Then the area of the parallelogram is equivalent to the absolute value of the determinant of a matrix built using a, b and c as rows with the last column padded using ones as follows:
. Then the area of the parallelogram is equivalent to the absolute value of the determinant of a matrix built using a, b and c as rows with the last column padded using ones as follows:
Proof that diagonals bisect each other
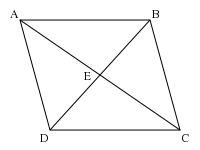
To prove that the diagonals of a parallelogram bisect each other, first note a few pairs of equivalent angles:
Since they are angles that a transversal makes with parallel lines 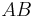 and
and 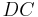 .
.
Also, 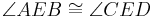 since they are a pair of vertical angles.
since they are a pair of vertical angles.
Therefore, 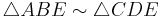 since they have the same angles.
since they have the same angles.
From this similarity, we have the ratios
Since 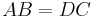 , we have
, we have
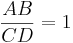 .
.
Therefore,
 bisects the diagonals
bisects the diagonals  and
and 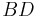 .
.
You can also prove that the diagonals bisect each other, by placing the parallelogram on a coordinate grid, and assign variables to the vertexes, you can show that the diagonals have the same midpoint.
Derivation of the area formula

The area formula,
can be derived as follows:
The area of the parallelogram to the right (the blue area) is the total area of the rectangle less the area of the two orange triangles. The area of the rectangle is
and the area of a single orange triangle is
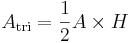 or
or 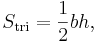
Therefore, the area of the parallelogram is
Alternate method


An alternative, less mathematically sophisticated method, to show the area is by rearrangement of the perimeter. First, take the two ends of the parallelogram and chop them off to form two more triangles. Each of these two new triangles are equal in every way with the orange triangles. This first step is shown to the right.
The second step is merely swap the left orange triangle with the right blue triangle. Clearly, the two blue triangles plus the blue rectangle have an area equivalent to 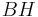 .
.
To further demonstrate this, the first image on the right could be printed off and cut up along the lines:
- Cut along the lines between the orange triangles and the blue parallelogram
- Cut along the vertical lines on the end to form the two blue triangles and the blue rectangle
- Rearrange all five pieces as shown in the second image
See also
- Fundamental parallelogram
- Parallelogram of force
- Rhombus
- Synthetic geometry
- Gnomon (figure)
External links
- Parallelogram and Rhombus - Animated course (Construction, Circumference, Area)
- Eric W. Weisstein, Parallelogram at MathWorld.
- Interactive Parallelogram --sides, angles and slope
- Area of Parallelogram at cut-the-knot
- Equilateral Triangles On Sides of a Parallelogram at cut-the-knot
- Varignon and Wittenbauer Parallelograms by Antonio Gutierrez from "Geometry Step by Step from the Land of the Incas"
- Van Aubel's theorem Quadrilateral with four squares by Antonio Gutierrez from "Geometry Step by Step from the Land of the Incas"
- Parallelogram Quiz
- Definition and properties of a parallelogram with animated applet
- Interactive applet showing parallelogram area calculation interactive applet