Parallel postulate

If the sum of the interior angles α and β is less than 180°, the two straight lines, produced indefinitely, meet on that side.

In geometry, the parallel postulate, also called Euclid's fifth postulate since it is the fifth postulate in Euclid's Elements, is a distinctive axiom in what is now called Euclidean geometry. It states that:

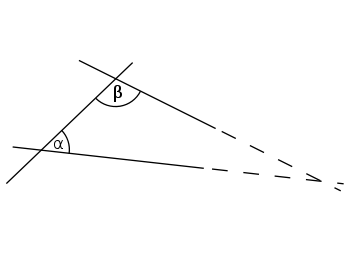
If a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.

Euclidean geometry is the study of geometry that satisfies all of Euclid's axioms, including the parallel postulate. A geometry where the parallel postulate cannot hold is known as a non-euclidean geometry. Geometry that is independent of Euclid's fifth postulate (i.e., only assumes the first four postulates) is known as absolute geometry (or, in other places known as neutral geometry).

Contents

Converse of Euclid's parallel postulate

If the sum of the two interior angles equals 180°, the lines are parallel and will never intersect.

Euclid did not postulate the converse of his fifth postulate, which is one way to distinguish Euclidean geometry from hyperbolic geometry. The Elements contains the proof of an equivalent statement (Book I, Proposition 17): Any two angles of a triangle are together less than two right angles. The proof depends on an earlier proposition: In a triangle ABC, the exterior angle at C is greater than either of the interior angles A or B. This in turn depends on Euclid's unstated assumption that two straight lines meet in only one point, a statement not true of elliptic geometry.

In other words, the converse of the fifth postulate follows from Euclid's axioms minus the fifth postulate, plus an axiom stating that two distinct non-parallel straight lines meet in only one point.

Logically equivalent properties

It is often stated that Euclid's parallel postulate is equivalent to Playfair's axiom, named after the Scottish mathematician John Playfair, which states:

Exactly one line can be drawn through any point not on a given line parallel to the given line in a plane.[1]

However this can be seen to be false because Euclid's parallel postulate is not inconsistent with elliptical geometry; two lines in an elliptical space intersected by a third line, forming two interior angles on one side with a sum less than two right angles, will meet on that side. That they meet on the other side as well does not contradict the parallel postulate. Playfair's axiom excludes this possibility by assuming that at least one parallel line through a given point does exist, which Euclid wrongly believed could be proven from his other postulates (Elements, Book 1 Proposition 31).

Many other equivalent statements to the parallel postulate or to Playfair's axiom have been suggested, some of them appearing at first to be unrelated to parallelism, and some seeming so self-evident that they were unconsciously assumed by people who claimed to have proven the parallel postulate from Euclid's other postulates.

  1. The sum of the angles in every triangle is 180°.
  2. There exists a triangle whose angles add up to 180°.
  3. The sum of the angles is the same for every triangle.
  4. There exists a pair of similar, but not congruent, triangles.
  5. Every triangle can be circumscribed.
  6. If three angles of a quadrilateral are right angles, then the fourth angle is also a right angle.
  7. There exists a quadrilateral of which all angles are right angles.
  8. There exists a pair of straight lines that are at constant distance from each other.
  9. Two lines that are parallel to the same line are also parallel to each other.
  10. Given two parallel lines, any line that intersects one of them also intersects the other.
  11. In a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides (Pythagoras' Theorem).
  12. There is no upper limit to the area of a triangle. [1]

However, the alternatives which employ the word "parallel" cease appearing so simple when one is obliged to explain which of the three common definitions of "parallel" is meant - constant separation, never meeting or same angles where crossed by a third line - since the equivalence of these three is itself one of the unconsciously obvious assumptions equivalent to Euclid's fifth postulate.

History

For two thousand years, many attempts were made to prove the parallel postulate using Euclid's first four postulates. The main reason that such a proof was so highly sought after was that the fifth postulate isn't self-evident unlike the other postulates. If the order the postulates were listed in the Elements is significant, it indicates that Euclid included this postulate only when he realised he could not prove it or proceed without it[2].

Omar Khayyám (1050-1123) recognized that three possibilities arose from omitting Euclid's Fifth; if two perpendiculars to one line cross another line, judicious choice of the last can make the internal angles where it meets the two perpendiculars equal (it is then parallel to the first line). If those equal internal angles are right angles, we get Euclid's Fifth; otherwise, they must be either acute or obtuse. He persuaded himself that the acute and obtuse cases lead to contradiction, but had made a tacit assumption equivalent to the fifth to get there.

Girolamo Saccheri (1667-1733) pursued the same line of reasoning more thoroughly, correctly obtaining absurdity from the obtuse case (proceeding, like Euclid, from the implicit assumption that lines can be extended indefinitely and have infinite length), but failing to debunk the acute case (although he managed to wrongly persuade himself that he had).

Where Saccheri and Khayyám had attempted to prove Euclid's fifth by disproving the only possible alternatives, the nineteenth century finally saw mathematicians exploring those alternatives and discovering the logically consistent geometries which result.

In 1829, Nikolai Ivanovich Lobachevsky published an account of acute geometry in an obscure Russian journal (later re-published in 1840 in German).

In 1831, János Bolyai included, in a book by his father, an appendix describing acute geometry, which, doubtlessly, he had developed independently of Lobachevsky.

Carl Friedrich Gauss had actually studied the problem before that, but he didn't have a courage to publish any of his results. [3]

The resulting geometries were later developed by Lobachevsky, Riemann and Poincaré into hyperbolic geometry (the acute case) and spherical geometry (the obtuse case).

The independence of the parallel postulate from Euclid's other axioms was finally demonstrated by Eugenio Beltrami in 1868.

Criticism

Attempts to logically prove this postulate, rather than the eighth axiom, were criticized by Schopenhauer, as described in Schopenhauer's criticism of the proofs of the Parallel Postulate.

See also

References

  1. ↑ Euclid's Parallel Postulate and Playfair's Axiom
  2. ↑ Florence P. Lewis (Jan 1920). "History of the Parallel Postulate". The American Mathematical Monthly 27 (1): 16–23. doi:10.2307/2973238. 
  3. ↑ Isaac Asimov, The left hand of the electron, pp 159.

Further reading