Overtone
An overtone is a natural resonance or vibration frequency of a system. Systems described by overtones are often sound systems, for example, blown pipes or plucked strings.
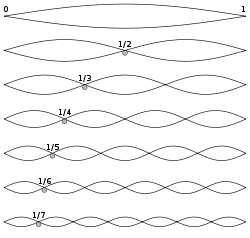
If such a system is excited, a number of sound frequencies may be produced. These frequencies are usually, but not always, a close approximation to an integer multiple of a lowest resonance frequency. Thus, overtones and harmonics should not be confused or interchanged. By definition a harmonic is an exact integer multiple of a fundamental frequency, whereas in most systems, overtones are never exact integer multiples of a root frequency. For example, the first overtone of a circular drum is approximately 2.4 times its fundamental resonance frequency.
Contents |
Explanation
Most oscillators, from a guitar string to a bell (or even the hydrogen atom or a periodic variable star) will naturally vibrate at a series of distinct frequencies known as normal modes. The lowest normal mode frequency is known as the fundamental frequency, while the higher frequencies are called overtones. Often, when these oscillators are excited, by, for example, plucking a guitar string, it will oscillate at several of its modal frequencies at the same time. So when a note is played, this gives the sensation of hearing other frequencies (overtones) above the lowest frequency (the fundamental).
Timbre is the quality that gives the listener the ability to distinguish between the sound of different instruments. The timbre of an instrument is determined by which overtones it emphasizes. That is to say, the relative volumes of these overtones to each other determines the specific "flavor" or "color" of sound of that family of instruments. The intensity of each of these overtones is rarely constant for the duration of a note. Over time, different overtones may decay at different rates, causing the relative intensity of each overtone to rise or fall independent of the overall volume of the sound. A carefully trained ear can hear these changes even in a single note. This is why the timbre of a note may be perceived differently when played staccato or legato.
A driven non-linear oscillator, such as the human voice, a blown wind instrument, or a bowed violin string (but not a struck guitar string or bell) will oscillate in a periodic, non-sinusoidal manner. This generates the impression of sound at integer multiple frequencies of the fundamental known as harmonics. For most string instruments and other long and thin instruments such as a trombone or bassoon, the first few overtones are quite close to integer multiples of the fundamental frequency, producing an approximation to a harmonic series. Thus, in music, overtones are often called harmonics. Depending upon how the string is plucked or bowed, different overtones can be emphasized.
However, some overtones in some instruments may not be of a close integer multiplication of the fundamental frequency, thus causing a small dissonance. "High quality" instruments are usually built in such a manner that their individual notes do not create disharmonious overtones. In fact, the flared end of a brass instrument is not to make the instrument sound louder, but to correct for tube length “end effects” that would otherwise make the overtones significantly different from integer harmonics. This is illustrated by the following:
Consider a guitar string. Its idealised 1st overtone would be exactly twice its fundamental if its length was shortened by ½, say by lightly pressing a guitar string at the 12th fret. However, if a vibrating string is examined, it will be seen that the string does not vibrate flush to the bridge and nut, but has a small “dead length” of string at each end. This dead length actually varies from string to string, being more pronounced with thicker and/or stiffer strings. This means that halving the physical string length does not halve the actual string vibration length, and hence, the overtones will not be exact multiples of a fundamental frequency. The effect is so pronounced that properly set up guitars will angle the bridge such that the thinner strings will progressively have a length up to few millimeters shorter than the thicker strings. Not doing so would result in inharmonious chords made up of two or more strings. Similar considerations apply to tube instruments.
Musical usage term
An 'overtone' is a partial (a "partial wave" or "constituent frequency") that can be either a harmonic or an inharmonic. A harmonic is an integer multiple of the fundamental frequency. An inharmonic overtone is a non-integer multiple of a fundamental frequency.
An example of harmonic overtones: (absolute harmony)
| f | 440 Hz | fundamental tone | first harmonic |
| 2f | 880 Hz | first overtone | second harmonic |
| 3f | 1320 Hz | second overtone | third harmonic |
| 4f | 1760 Hz | third overtone | fourth harmonic |
Not all overtones are necessarily harmonics, or exact multiples of the fundamental frequency. Some musical instruments produce overtones that are slightly sharper or flatter than the true harmonics. The sharpness or flatness of their overtones is one of the elements that contributes to their unique sound. This also has the effect of making their waveforms not perfectly periodic. Some instruments, such as tuning forks or flutes produce a clear or near perfect sound because their overtones are in very good approximation of "absolute" harmony with the base frequency.
Etymology
In Helmholtz' classic "On The Sensations Of Tone" he used the German "obertöne" which was actually a contraction of "oberpartialtöne", or in English: "upper partial tone". However, due to the similarity of German "ober" to English "over", a Prof. Tyndall mistranslated Helmholtz' term, thus creating "overtone." This created unfortunate confusion, adding an additional term that is somewhat unclear and has unfortunate mystical connotations. This has also led to the idea that if there are overtones, perhaps there are "undertones" - which is a term sometimes confused with "difference tones". In contrast, the correct translation of "upper partial tones" does not imply anything else other than the initial fundamental. Alexander Ellis, on pages 24-25 of his definitive English translation of Helmholtz, makes clear all the unfortunate confusion of this mistranslation which entered common usage. Ellis strongly suggests the avoidance of this term.
"Overtones" in barbershop music
In barbershop music, the word overtone is often used in a different (though related) way. It refers to a psychoacoustic effect in which a listener hears an audible pitch that is higher than, and different from, the four pitches being sung by the quartet. This is not a standard dictionary usage of the word "overtone." The barbershopper's "overtone" is created by the interactions of the overtones in each singer's note (and by sum and difference frequencies created by nonlinear interactions within the ear). Similar effects can be found in other a cappella polyphonic music such as the music of the Republic of Georgia.
String instruments
String instruments can also produce multiphonic tones when strings are divided in two pieces. The most developed instrument for playing multiphonic tones is the Sitar in which there are sympathetic strings which help to bring out the overtones while one is playing. The most well-known technique on a guitar is playing flageolet tones. Other multiphonic extended techniques used are prepared piano, prepared guitar and 3rd bridge.
Overtone singing
Overtone singing, also called harmonic singing, occurs when the singer amplifies voluntarily two overtones in the sequence available given the fundamental tone he/she is singing. Overtone singing (wrongly known also as throat singing), is a traditional form of singing in many parts of the Himalayas and Altay; Tibetans, Mongols and Tuvans are known for their overtone singing. Also, harmonics change the overtones.
Jew's harp
A similar technique is used for playing the Jew's harp: the performer amplifies the instrument's overtones by changing the shape, and therefore the resonance, of their mouth.
See also
- Harmonic series (music)
- Just intonation
- Xenharmonic
- Stretched octave
- Combination tone
- Electronic tuner