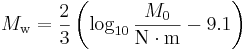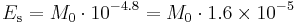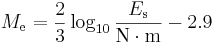Moment magnitude scale

The moment magnitude scale (or "MMS") is used by seismologists to measure the size of earthquakes in terms of the energy released[1]. The scale was developed in the 1970s as a successor to 1930s-era Richter magnitude scale. While the name of this scale is still relatively unfamiliar to the general public, the values are very familiar. For example, this is the scale used in press releases for all modern large earthquakes by the United States Geological Survey[2].

Like the Richter scale, the MMS is logarithmic, so an earthquake one number higher on the scale is approximately thirty times more powerful (e.g. a 7.0 vs. a 6.0).

Contents

Compared to Richter Scale

Comparison of the various scales used to estimate earthquake magnitudes

In 1935, Charles Richter developed the Local Magnitude scale (aka "the Richter scale") with the goal of quantifying medium-sized earthquakes (between magnitude 3.0 and 7.0) in Southern California. However, the original Richter formula does not give reliable estimates of earthquake size for large earthquakes with magnitudes over 7, nor does it work well for measurements taken at a distance of more than about 350 miles (600 km) from the earthquake's epicenter.[2]. The Moment Magnitude scale was introduced, in 1979 by Harvard University seismologists Thomas C. Hanks and Hiroo Kanamori, to address these shortcomings while maintaining consistency. Thus, for medium-sized earthquakes, the MMS values should be the same as Richter values. That is, a magnitude 6.0 earthquake will still be a 6.0 on either scale.

One advantage of the Moment Magnitude scale is that, unlike other magnitude scales, it does not saturate at the upper end. That is, there is no particular value beyond which all large earthquakes have about the same magnitude.

Like many mathematical formulas used to model the physical world, the gain at one end of the model has a cost at the other—the moment magnitude scale is relatively unrevealing (and hence inappropriate) for smaller, lighter and more common quakes. For this reason, moment magnitude is now the most common estimate of both medium and large earthquake magnitudes[3], but is rarely used for smaller quakes. For example, the United States Geological Survey does not use this scale for earthquakes with a magnitude of less than 3.5, which is the great majority of quakes. For these smaller quakes, other magnitude scales similar to the Richter scale are used.

It should be noted, however, that the 1930s Richter Scale has been tweaked and adjusted repeatedly over the ensuing decades. When the press now reports an earthquake's magnitude, readers may assume it was calculated with the original Richter formula, when in fact it most often is not.[3] Thus, it is valuable to make a separation between:

It should also be noted that neither the Moment scale formula nor the Richter scale formula measures the so-called earthquake intensity, which is the perceptible moving, shaking, and local damages experienced during a quake. The shaking intensity at a given spot depends on many factors, such as soil types, soil sublayers, depth, type of displacement, and range from the epicenter (not counting the complications of building engineering and architectural factors). Rather, both the Moment magnitude scale and the Richter scale are used to measure (or rather, estimate) only the total energy released by the quake.

Mathematical derivation

The symbol for the moment magnitude scale is 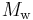M_\mathrm{w}, with the subscript w meaning mechanical work accomplished. The moment magnitude 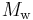M_\mathrm{w} is a dimensionless number defined by

M_\mathrm{w} = {2 \over 3}\left(\log_{10} \frac{M_0}{\mathrm{N}\cdot \mathrm{m}} - 9.1\right)

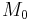where M_0 is the seismic moment. The division by N·m has the effect of indicating that the seismic moment is to be expressed in newton meters before the logarithm is taken; see ISO 31-0. The constant values in the equation are chosen to achieve consistancy with the magnitude values produced by earlier scales, most importantly the Local Moment (or "Richter") scale.

As with the Richter scale, an increase of 1 step on this logarithmic scale corresponds to a 101.5 = 31.6 times increase in the amount of energy released, and an increase of 2 steps corresponds to a 103 = 1000 times increase in energy.

Radiated seismic energy

Potential energy is stored in the crust in the form of built-up stress. During an earthquake, this stored energy is transformed and results in

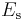The seismic moment 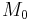M_0 is a measure of the total amount of energy that is transformed during an earthquake. Only a small fraction of the seismic moment 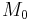M_0 is converted into radiated seismic energy 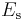E_\mathrm{s}, which is what seismographs register. Using the estimate

E_\mathrm{s} = M_0 \cdot 10^{-4.8} = M_0 \cdot 1.6\times 10^{-5}

Choy and Boatwright defined in 1995 the energy magnitude

M_\mathrm{e} = {2 \over 3}\log_{10} \frac{E_\mathrm{s}}{\mathrm{N}\cdot \mathrm{m}} - 2.9

Nuclear explosions

The energy released by nuclear weapons is traditionally expressed in terms of the energy stored in a kiloton or megaton of the conventional explosive trinitrotoluene (TNT).

Many academics refer to a 1 kt TNT explosion being roughly equivalent to a magnitude 4 earthquake (an often quoted rule of thumb in seismology), which in turn leads to the equation

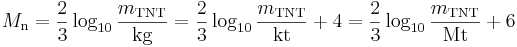M_\mathrm{n} = {2 \over 3}\log_{10} \frac{m_{\mathrm{TNT}}}{\mbox{kg}} = {2 \over 3}\log_{10} \frac{m_{\mathrm{TNT}}}{\mbox{kt}} + 4 = {2 \over 3}\log_{10} \frac{m_{\mathrm{TNT}}}{\mbox{Mt}} + 6.

where 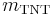m_{\mathrm{TNT}} is the mass of the explosive TNT that is quoted for comparison.

Such comparison figures are not very meaningful. As with earthquakes, during an underground explosion of a nuclear weapon, only a small fraction of the total amount of energy transformed ends up being radiated as seismic waves. Therefore, a seismic efficiency has to be chosen for a bomb that is quoted as a comparison. Using the conventional specific energy of TNT (4.184 MJ/kg), the above formula implies the assumption that about 0.5% of the bomb's energy is converted into radiated seismic energy 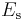E_\mathrm{s}. For real underground nuclear tests, the actual seismic efficiency achieved varies significantly and depends on the site and design parameters of the test.

See also

External links

References

  1. ↑ Hanks, Thomas C.; Kanamori, Hiroo (05/1979). "Moment magnitude scale". Journal of Geophysical Research 84 (B5): 2348–2350. doi:10.1029/JB084iB05p02348. http://adsabs.harvard.edu/abs/1979JGR....84.2348H. Retrieved on 2007-10-06. 
  2. ↑ 2.0 2.1 USGS Earthquake Magnitude Policy
  3. ↑ 3.0 3.1 Boyle, Alan (May 12, 2008). "Quakes by the numbers". MSNBC. Retrieved on 2008-05-12. "That original scale has been tweaked through the decades, and nowadays calling it the "Richter scale" is an anachronism. The most common measure is known simply as the moment magnitude scale."

Sources

Seismic scales
Modern scales
Intensity scales
European Macroseismic Scale (EMS) | INQUA | Liedu | Medvedev-Sponheuer-Karnik (MSK) | Modified Mercalli (MM) | Shindo
Magnitude scales
Body wave magnitude | Local magnitude (Richter scale) | Moment magnitude | Surface wave magnitude
Historical scales
Mercalli-Cancani-Sieberg (MCS) | Mercalli-Wood-Neuman (MWN) | Omori | Rossi-Forel