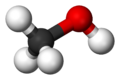
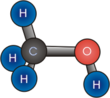
Molecular geometry

Geometry of the water molecule

Molecular geometry or molecular structure is the three-dimensional arrangement of the atoms that constitute a molecule. It determines several properties of a substance including its reactivity, polarity, phase of matter, color, magnetism, and biological activity.^{[1] [2]}

Molecular geometry determination

The molecular geometry can be determined by various spectroscopic methods and diffraction methods. IR, Microwave and Raman spectroscopy can give information about the molecule geometry from the details of the vibrational and rotational absorbances detected by these techniques. X-ray crystallography, neutron diffraction and electron diffraction can give molecular structure for crystalline solids based on the distance between nuclei and concentration of electron density. Gas electron diffraction can be used for small molecules in the gas phase. NMR and FRET methods can be used to determine complentary information including relative distances, ^[3][4][5] dihedral angles, ^{[6] [7]} angles, and connectivity. Molecular geometries are best determined at low temperature because at higher temperatures the molecular structure is averaged over more accessible geometries (see next section). Larger molecules often exist in multiple stable geometries (conformational isomerism) that are close in energy on the potential energy surface. Geometries can also be computed by ab initio quantum chemistry methods to high accuracy. The molecular geometry can be different as a solid, in solution, and as a gas.

The position of each atom is determined by the nature of the chemical bonds by which it is connected to its neighboring atoms. The molecular geometry can be described by the positions of these atoms in space, evoking bond lengths of two joined atoms, bond angles of three connected atoms, and torsion angles (dihedral angles) of three consecutive bonds.

The influence of thermal excitation

Since the motions of the atoms in a molecule are determined by quantum mechanics, one must define “motion” in a quantum mechanical way. The overall (external) quantum mechanical motions translation and rotation hardly change the geometry of the molecule. (To some extent rotation influences the geometry via Coriolis forces and centrifugal distortion, but this is negligible for the present discussion.) A third type of motion is vibration, which is the internal motion of the atoms in a molecule. The molecular vibrations are harmonic (at least to good approximation), which means that the atoms oscillate about their equilibrium, even at the absolute zero of temperature. At absolute zero all atoms are in their vibrational ground state and show zero point quantum mechanical motion, that is, the wavefunction of a single vibrational mode is not a sharp peak, but an exponential of finite width. At higher temperatures the vibrational modes may be thermally excited (in a classical interpretation one expresses this by stating that “the molecules will vibrate faster”), but they oscillate still around the recognizable geometry of the molecule.

To get a feeling for the probability that the vibration of molecule may be thermally excited, we inspect the Boltzmann factor 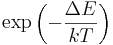, where 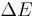is the excitation energy of the vibrational mode, 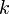the Boltzmann constant and the absolute temperature. At 298K (25 °C), typical values for the Boltzmann factor are: ΔE = 500 cm^-1 --> 0.089; ΔE = 1000 cm^-1 --> 0.008; ΔE = 1500 cm^-1 --> 7 10^-4. That is, if the excitation energy is 500 cm^-1, then about 9% of the molecules are thermally excited at room temperature. The lowest excitation vibrational energy in water is the bending mode (about 1600 cm^-1). Thus, at room temperature less than 0.07% of all the molecules of a given amount of water will vibrate faster than at absolute zero.

As stated above, rotation hardly influences the molecular geometry. But, as a quantum mechanical motion, it is thermally excited at relatively (as compared to vibration) low temperatures. From a classical point of view it can be stated that more molecules rotate faster at higher temperatures, i.e., they have larger angular velocity and angular momentum. In quantum mechanically language: more eigenstates of higher angular momentum become thermally populated with rising temperatures. Typical rotational excitation energies are on the order of a few cm^-1.

The results of many spectroscopic experiments are broadened because they involve an averaging over rotational states. It is often difficult to extract geometries from spectra at high temperatures, because the number of rotational states probed in the experimental averaging increases with increasing temperature. Thus, many spectroscopic observations can only be expected to yield reliable molecular geometries at temperatures close to absolute zero, because at higher temperatures too many higher rotational states are thermally populated.

Bonding

Molecules, by definition, are most often held together with covalent bonds involving single, double, and/or triple bonds, where a "bond" is a shared pair of electrons (the other method of bonding between atoms is called ionic bonding and involves a positive cation and a negative anion).

Molecular geometries can be specified in terms of bond lengths, bond angles and torsional angles. The bond length is defined to be the average distance between the centers of two atoms bonded together in any given molecule. A bond angle is the angle formed between three atoms across at least two bonds. For four atoms bonded together in a straight chain, the torsional angle is the angle between the plane formed by the first three atoms and the plane formed by the last three atoms.

Molecular geometry is determined by the quantum mechanical behavior of the electrons. Using the valence bond approximation this can be understood by the type of bonds between the atoms that make up the molecule. When atoms interact to form a chemical bond, the atomic orbitals are said to mix in a process called orbital hybridisation. The two most common types of bonds are Sigma bonds and Pi bonds. The geometry can also be understood by molecular orbital theory where the electrons are delocalised.

An understanding of the wavelike behavior of electrons in atoms and molecules is the subject of quantum chemistry.

Isomers

Isomers are types of molecules that share a chemical formula but have different geometries, resulting in very different properties:

• A pure substance is composed of only one type of isomer of a molecule (all have the same geometrical structure).

• Structural isomers have the same chemical formula but different physical arrangements, often forming alternate molecular geometries with very different properties. The atoms are not bonded (connected) together in the same orders.
  • Functional isomers are special kinds of structural isomers, where certain groups of atoms exhibit a special kind of behavior, such as an ether or an alcohol.

• Stereoisomers may have many similar physicochemical properties (melting point, boiling point) and at the same time very different biochemical activities. This is because they exhibit a handedness that is commonly found in living systems. One manifestation of this chirality or handedness is that they have the ability to rotate polarized light in different directions.

• Protein folding concerns the complex geometries and different isomers that proteins can take.

Types of molecular structure

Main article: VSEPR Theory#AXE Method

There are six basic shape types for molecules

• Linear: In a linear model, atoms are connected in a straight line. The bond angles are set at 180°. A bond angle is very simply the geometric angle between two adjacent bonds. For example, carbon dioxide has a linear molecular shape.
• Trigonal planar: Just from its name, it can easily be said that molecules with the trigonal planar shape are somewhat triangular and in one plane (meaning a flat surface). Consequently, the bond angles are set at 120°. An example of this is boron trifluoride.
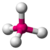
• Tetrahedral: Tetra- signifies four, and -hedral relates to a surface, so tetrahedral almost literally means "four surfaces." This is when there are four bonds all on one central atom, with no extra unshared electron pairs. In accordance with the VSEPR (valence-shell electron pair repulsion theory), the bond angles between the electron bonds are 109.5°. An example of a tetrahedral molecule is methane (CH₄).
• Octahedral: Octa- signifies eight, and -hedral relates to a surface, so octahedral almost literally means "eight surfaces." The bond angle is 90 degrees. An example of an octahedral molecule is sulfur hexafluoride (SF₆).
• Pyramidal: Pyramidal-shaped molecules have pyramid-like shapes. Unlike the linear and trigonal planar shapes but similar to the tetrahedral orientation, pyramidal shapes requires three dimensions in order to fully separate the electrons. Here, there are only three pairs of bonded electrons, leaving one unshared lone pair. Lone pair - bond pair repulsions change the angle from the tetrahedral angle to a slightly lower value. An example is NH₃ (ammonia).
• Bent: The final basic shape of a molecule is the non-linear shape, also known as bent or angular. One of the most unquestionably important molecules any chemist studies is water, or H₂O. A water molecule has a non-linear shape because it has two pairs of bonded electrons and two unshared lone pairs. Like in the other arrangements, electrons must be spaced as far as possible. Lone pair - bond pair repulsions push the angle from the tetrahedral angle down to around 106°.

VSEPR Table

Outer Atoms	Lone Pairs	Charge Clouds	Shape	Ideal Bond Angle	Example	Image
2	0	2	linear	180°	BeCl2
3	0	3	trigonal planar	120°	BF3
2	1	3	bent	120°	SO2
4	0	4	tetrahedral	109.5°	CH4
3	1	4	trigonal pyramidal	109.5°	NH3
2	2	4	bent	109.5°	H2O
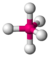
5	0	5	trigonal bipyramidal	90°, 120°	PCl5
4	1	5	seesaw	90°, 120°	SF4
3	2	5	T-shaped	90°	ClF3
2	3	5	linear	180°	XeF2
6	0	6	octahedral	90°	SF6
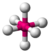5	1	6	square pyramidal	90°	BrF5
4	2	6	square planar	90°	XeF4

3-D Specification

• Z-matrix (chemistry)
• Atomic coordinates and connection tables as found in the pdb file format
• Atomic Fractional coordinates
• Atomic Cartesian coordinates

3-D Representations

• Line or stick - atomic nuclei are not represented, just the bonds as sticks or lines

• Electron density plot - shows the electron density determined either crystallographically or using quantum mechanics rather than distinct atoms or bonds

• Ball and stick - atomic nuclei are represented by spheres (balls) and the bonds as sticks

• Spacefilling models or CPK models (also an atomic coloring scheme in representations) - the molecule is represented by overlapping spheres representing the atoms

• Cartoon - a representation used for proteins where loops, beta sheets, alpha helices are represented diagrammatically and no atoms or bonds are represented explicitly just the protein backbone as a smooth pipe

See also

• VSEPR theory
• Molecular graphics

References