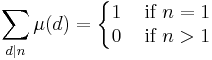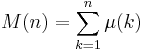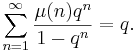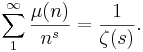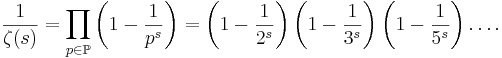Möbius function

For the rational functions defined on the complex numbers, see Möbius transformation.

The classical Möbius function μ(n) is an important multiplicative function in number theory and combinatorics. It is named in honor of the German mathematician August Ferdinand Möbius, who first introduced it in 1831. This classical Möbius function is a special case of a more general object in combinatorics (see below).

Definition

μ(n) is defined for all positive integers n and has its values in {−1, 0, 1} depending on the factorization of n into prime factors. It is defined as follows:

This is taken to imply that μ(1) = 1. The value of μ(0) is generally left undefined.

Values of μ(n) for the first 25 positive numbers (sequence A008683 in OEIS):

1, −1, −1, 0, −1, 1, −1, 0, 0, 1, −1, 0, −1, 1, 1, 0, −1, 0, −1, 0, 1, 1, −1, 0, 0, ...

The 50 first values of the function are plotted below:

The 50 first values of the function

Properties and applications

The Möbius function is multiplicative (i.e. μ(ab) = μ(a) μ(b) whenever a and b are coprime). The sum over all positive divisors of n of the Möbius function is zero except when n = 1:

\sum_{d | n} \mu(d) = \left\{\begin{matrix}1&\mbox{ if } n=1\\ 0&\mbox{ if } n>1\end{matrix}\right.

(A consequence of the fact that every non-empty finite set has just as many subsets with an even number of elements as it has subsets with an odd number of elements.) This leads to the important Möbius inversion formula and is the main reason why μ is of relevance in the theory of multiplicative and arithmetic functions.

Other applications of μ(n) in combinatorics are connected with the use of the Pólya enumeration theorem in combinatorial groups and combinatorial enumerations.

In number theory another arithmetic function closely related to the Möbius function is the Mertens function, defined by

M(n) = \sum_{k = 1}^n \mu(k)

for every natural number n. This function is closely linked with the positions of zeroes of the Riemann zeta function. See the article on the Mertens conjecture for more information about the connection between M(n) and the Riemann hypothesis.

The Lambert series for the Möbius function is

\sum_{n=1}^\infty \frac{\mu(n)q^n}{1-q^n} = q.

The Dirichlet series that generates the Möbius function is the (multiplicative) inverse of the Riemann zeta function

\sum_1^\infty \frac{\mu(n)}{n^s}=\frac{1}{\zeta(s)}.

This is easy to see from its Euler product

\frac{1}{\zeta(s)} = \prod_{p\in \mathbb{P}}{\left(1-\frac{1}{p^{s}}\right)}= \left(1-\frac{1}{2^{s}}\right)\left(1-\frac{1}{3^{s}}\right)\left(1-\frac{1}{5^{s}}\right)\dots.

μ(n) sections

μ(n) = 0 if and only if n is divisible by a square. The first numbers with this property are (sequence A013929 in OEIS):

4, 8, 9, 12, 16, 18, 20, 24, 25, 27, 28, 32, 36, 40, 44, 45, 48, 49, 50, 52, 54, 56, 60, 63,...

If n is prime, then μ(n) = −1, but the converse is not true. The first non prime n for which μ(n) = −1 is 30 = 2·3·5. The first such numbers with three distinct prime factors (sphenic numbers) are:

30, 42, 66, 70, 78, 102, 105, 110, 114, 130, 138, 154, 165, 170, 174, 182, 186, 190, 195, 222, … (sequence A007304 in OEIS)

and the first such numbers with 5 distinct prime factors are:

2310, 2730, 3570, 3990, 4290, 4830, 5610, 6006, 6090, 6270, 6510, 6630, 7410, 7590, 7770, 7854, 8610, 8778, 8970, 9030, 9282, 9570, 9690, … (sequence A046387 in OEIS)

Generalization

In combinatorics, every locally finite partially ordered set (poset) is assigned an incidence algebra. One distinguished member of this algebra is that poset's "Möbius function". The classical Möbius function treated in this article is essentially equal to the Möbius function of the set of all positive integers partially ordered by divisibility. See the article on incidence algebras for the precise definition and several examples of these general Möbius functions.

Physics

The Möbius function also arises in the primon gas or free Riemann gas model of supersymmetry. In this theory, the fundamental particles or "primons" have energies log p. Under second-quantization, multiparticle excitations are considered; these are given by log n for any natural number n. This follows from the fact that the factorization of the natural numbers into primes is unique.

In the free Riemann gas, any natural number can occur, if the primons are taken as bosons. If they are taken as fermions, then the Pauli exclusion principle excludes squares. The operator (−1)F which distinguishes fermions and bosons is then none other than the Möbius function μ(n).

The free Riemann gas has a number of other interesting connections to number theory, including the fact that the partition function is the Riemann zeta function. This idea underlies Alain Connes' attempted proof of the Riemann hypothesis. [1]

See also

References

  1. ↑ J.-B. Bost and Alain Connes (1995), "Hecke Algebras, Type III factors and phase transitions with spontaneous symmetry breaking in number theory", Selecta Math. (New Series), 1 411-457.