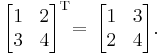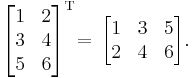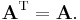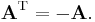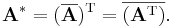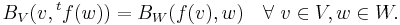Transpose
- This article is about the Matrix Transpose operator. For other uses, see Transposition
In linear algebra, the transpose of a matrix A is another matrix AT (also written Atr, tA, or A′) created by any one of the following equivalent actions:
- write the rows of A as the columns of AT
- write the columns of A as the rows of AT
- reflect A by its main diagonal (which starts from the top left) to obtain AT
Formally, the transpose of an m × n matrix A is the n × m matrix
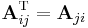 for
for 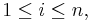
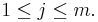
Contents |
Examples
Properties
For matrices A, B and scalar c we have the following properties of transpose:
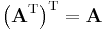
- Taking the transpose is an involution (self inverse).
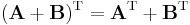
- The transpose is a linear map from the space of m × n matrices to the space of all n × m matrices.

- Note that the order of the factors reverses. From this one can deduce that a square matrix A is invertible if and only if AT is invertible, and in this case we have (A−1)T = (AT)−1. It is relatively easy to extend this result to the general case of multiple matrices, where we find that (ABC...XYZ)T = ZTYTXT...CTBTAT.
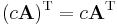
- The transpose of a scalar is the same scalar.
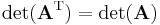
- The determinant of a matrix is the same as that of its transpose.
- The dot product of two column vectors a and b can be computed as
- If A has only real entries, then ATA is a positive-semidefinite matrix.
- If A is over some field, then A is similar to AT.
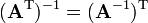
- The transpose of an invertible matrix is also invertible, and its inverse is the transpose of the inverse of the original matrix.
- If A is a square matrix, then its eigenvalues are equal to the eigenvalues of its transpose.
Special transpose matrices
A square matrix whose transpose is equal to itself is called a symmetric matrix; that is, A is symmetric if
A square matrix whose transpose is also its inverse is called an orthogonal matrix; that is, G is orthogonal if
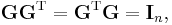 the identity matrix, i.e. GT = G-1.
the identity matrix, i.e. GT = G-1.
A square matrix whose transpose is equal to its negative is called skew-symmetric matrix; that is, A is skew-symmetric if
The conjugate transpose of the complex matrix A, written as A*, is obtained by taking the transpose of A and the complex conjugate of each entry:
Transpose of linear maps
If f: V→W is a linear map between vector spaces V and W with nondegenerate bilinear forms, we define the transpose of f to be the linear map tf : W→V, determined by
Here, BV and BW are the bilinear forms on V and W respectively. The matrix of the transpose of a map is the transposed matrix only if the bases are orthonormal with respect to their bilinear forms.
Over a complex vector space, one often works with sesquilinear forms instead of bilinear (conjugate-linear in one argument). The transpose of a map between such spaces is defined similarly, and the matrix of the transpose map is given by the conjugate transpose matrix if the bases are orthonormal. In this case, the transpose is also called the Hermitian adjoint.
If V and W do not have bilinear forms, then the transpose of a linear map f: V→W is only defined as a linear map tf : W*→V* between the dual spaces of W and V.
Implementation of matrix transposition on computers
On a computer, one can often avoid explicitly transposing a matrix in memory by simply accessing the same data in a different order. For example, software libraries for linear algebra, such as BLAS, typically provide options to specify that certain matrices are to be interpreted in transposed order to avoid the necessity of data movement.
However, there remain a number of circumstances in which it is necessary or desirable to physically reorder a matrix in memory to its transposed ordering. For example, with a matrix stored in row-major order, the rows of the matrix are contiguous in memory and the columns are discontiguous. If repeated operations need to be performed on the columns, for example in a fast Fourier transform algorithm, transposing the matrix in memory (to make the columns contiguous) may improve performance by increasing memory locality.
Ideally, one might hope to transpose a matrix with minimal additional storage. This leads to the problem of transposing an N × M matrix in-place, with O(1) additional storage or at most storage much less than MN. For N ≠ M, this involves a complicated permutation of the data elements that is non-trivial to implement in-place. Therefore efficient in-place matrix transposition has been the subject of numerous research publications in computer science, starting in the late 1950s, and several algorithms have been developed.
External links
- MIT Video Lecture on Matrix Transposes at Google Video, from MIT OpenCourseWare
- Transpose, mathworld.wolfram.com
- Transpose, planetmath.org
|
|||||