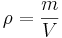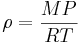Density

The density of a material is defined as its mass per unit volume:

$\rho = \frac{m}{V}$

Different materials usually have different densities, so density is an important concept regarding buoyancy, metal purity and packaging.

In some cases density is expressed as the dimensionless quantities specific gravity or relative density, in which case it is expressed in multiples of the density of some other standard material, usually water or air.

1 History
2 Measurement of density
3 Common units
4 Changes of density
5 Density of water
6 Density of air
7 Density of solutions
8 Density of composite material
9 Densities of various materials
10 References
11 See also
12 External links

History

In a well-known story, Archimedes was given the task of determining whether King Hiero's goldsmith was embezzling gold during the manufacture of a wreath dedicated to the gods and replacing it with another, cheaper alloy.^[1]

Archimedes knew that the irregularly shaped wreath could be crushed into a cube whose volume could be calculated easily and compared with the weight; but the king did not approve of this.

Baffled, Archimedes took a bath and observed from the rise of the water upon entering that he could calculate the volume of the crown through the displacement of the water. Allegedly, upon this discovery, he went running naked though the streets shouting, "Eureka! Eureka!" (Greek "I found it"). As a result, the term "eureka" entered common parlance and is used today to indicate a moment of enlightenment.

This story first appeared in written form in Vitruvius' books of architecture, two centuries after it supposedly took place.^[2] Some scholars have doubted the accuracy of this tale, saying among other things that the method would have required precise measurements that would have been difficult to make at the time. ^[3]^[4]

Measurement of density

For a homogeneous object, the mass divided by the volume gives the density. The mass is normally measured with an appropriate scale or balance; the volume may be measured directly (from the geometry of the object) or by the displacement of a fluid.

If the body is inhomogeneous, the density is a function of the coordinates 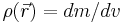$\rho(\vec{r})=dm/dv$ , where 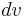$dv$ is elementary volume with coordinates 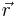$\vec{r}$ . The mass of the body then can be expressed as

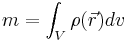$m = \int_V \rho(\vec{r})dv$ ,

where the integration is over the volume of the body V.

A very common instrument for the direct measurement of the density of a liquid is the hydrometer, which measures the volume displaced by an object of known mass. A common laboratory device for measuring fluid density is a pycnometer; a related device for measuring the absolute density of a solid is a gas pycnometer. Another instrument used to determine the density of a liquid or a gas is the digital density meter - based on the oscillating U-tube principle.

The density of a solid material can be ambiguous, depending on exactly how its volume is defined, and this may cause confusion in measurement. A common example is sand: if gently filled into a container, the density will be low; when the same sand is compacted into the same container, it will occupy less volume and consequently exhibit a greater density. This is because sand, like all powders and granular solids contains a lot of air space in between individual grains; this overall density is called the bulk density, which differs significantly from the density of an individual grain of sand.

Common units

The SI unit for density is:

kilograms per cubic metre (kg/m³)

Metric units outside the SI

kilograms per litre (kg/L). Water generally has a density around 1 kg/L, making this a convenient unit.
kilograms per cubic decimeter (kg/dm³)
grams per millilitre (g/mL),
grams per cubic centimeter (g/cc or g/cm³).

These are numerically equivalent to kg/L (1 kg/L = 1 kg/dm³ = 1 g/cm³ = 1 g/mL).

In U.S. customary units or Imperial units, the units of density include:

ounces per cubic inch (oz/cu in)
pounds per cubic inch (lb/cu in)
pounds per cubic foot (lb/cu ft)
pounds per cubic yard (lb/cu yd)
pounds per gallon (for U.S. or imperial gallons) (lb/gal)
pounds per U.S. bushel (lb/bu)
slugs per cubic foot.

Changes of density

In general density can be changed by changing either the pressure or the temperature. Increasing the pressure will always increase the density of a material. Increasing the temperature generally decreases the density, but there are notable exceptions to this generalisation. For example, the density of water increases between its melting point at 0 °C and 4 °C and similar behaviour is observed in silicon at low temperatures.

The effect of pressure and temperature on the densities of liquids and solids is small so that a typical compressibility for a liquid or solid is 10^–6 bar^–1 (1 bar=0.1 MPa) and a typical thermal expansivity is 10^–5 K^–1.

In contrast, the density of gases is strongly affected by pressure. Boyle's law says that the density of an ideal gas is given by

$\rho = \frac {MP}{RT}$

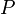where $R$ is the universal gas constant, $P$ is the pressure, 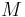$M$ the molar mass, and $T$ the absolute temperature.

This means that a gas at 300 K and 1 bar will have its density doubled by increasing the pressure to 2 bar or by reducing the temperature to 150 K.

Iridium is the densest known substance at standard conditions for temperature and pressure.

Density of water

Temp (°C)	Density (g/cm³)
100	0.9584
80	0.9718
60	0.9832
40	0.9922
30	0.9956502
25	0.9970479
22	0.9977735
20	0.9982071
15	0.9991026
10	0.9997026
4	0.9999720
0	0.9998395
−10	0.998117
−20	0.993547
−30	0.983854
The density of water in grams per cubic centimeter at various temperatures in degrees Celsius^[5] The values below 0 °C refer to supercooled water. Water - Density and Specific Weight

See Water Density

Density of air

T in °C	ρ in kg/m³ (at 1 atm)
–10	1.342
–5	1.316
0	1.293
5	1.269
10	1.247
15	1.225
20	1.204
25	1.184
30	1.165

Density of solutions

The density of a solution is the sum of the mass (massic) concentrations of the components of that solution. Mass (massic) concentration of a given component ρ_i in a solution can be called partial density of that component.

Density of composite material

ASTM specification D792-00^[6] describes the steps to measure the density of a composite material.

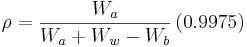
$\rho = \frac{W_a}{W_a + W_w - W_b} \left (0.9975 \right ) \$

where:

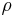$\rho$ is the density of the composite material, in g/cm³

and

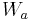$W_a$ is the weight of the specimen when hung in the air

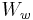$W_w$ is the weight of the specimen when immersed fully in distilled water, along with the partly immersed wire holding the specimen

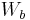$W_b$ is the weight of the partly immersed wire holding the specimen

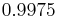$0.9975$ is the density in g/cm³ of the distilled water at 23°C

Densities of various materials

Material	ρ in kg/m³	Notes
Interstellar medium	10^-25 − 10^-15	Assuming 90% H, 10% He; variable T
Earth's atmosphere	1.2	At sealevel
Aerogel	1 − 2
Styrofoam	30 − 120	From
Cork	220 − 260	From
Water	1000	At STP
Plastics	850 − 1400	For polypropylene and PETE/PVC
The Earth	5515.3	Mean density
Copper	8920 − 8960	Near room temperature
Lead	11340	Near room temperature
The Inner Core	~13000	As listed in Earth
Uranium	19100	Near room temperature
Iridium	22500	Near room temperature
The core of the Sun	~150000
Atomic nuclei	~3 × 10¹⁷	As listed in neutron star
Neutron star	8.4 × 10¹⁶ − 1 × 10¹⁸
Black hole	2 × 10³⁰	Mean density inside the Schwarzschild radius of an earth-mass black hole (theoretical)

References

↑ Archimedes, A Gold Thief and Buoyancy - by Larry "Harris" Taylor, Ph.D.
↑ Vitruvius on Architecture, Book IX, paragraphs 9-12, translated into English and in the original Latin.
↑ The first Eureka moment, Science 305: 1219, August 2004.
↑ Fact or Fiction?: Archimedes Coined the Term "Eureka!" in the Bath, Scientific American, December 2006.
↑ Lide, D. R. (Ed.) (1990). CRC Handbook of Chemistry and Physics (70th Edn.). Boca Raton (FL):CRC Press.
↑ (2004). Test Methods for Density and Specific Gravity (Relative Density) of Plastics by Displacement. ASTM Standard D792-00. Vol 81.01. American Society for Testing and Materials. West Conshohocken. PA.